Tensors for Beginners 1: Forward and Backward Transformations (REMAKE)
TLDRThis video introduces forward and backward transformations in tensors, essential for moving between different coordinate systems. It explains how to construct new basis vectors from old ones using linear combinations and matrices. The video also shows that the forward and backward matrices are inverses, forming the identity matrix when multiplied. The discussion includes a generalization to n dimensions and the introduction of the Kronecker Delta symbol. The next video will explore vector components and their transformations.
Takeaways
- 📚 The video introduces the concept of forward and backward transformations, which are essential for understanding how to move between different coordinate systems in the context of tensors.
- 🔄 Forward transformation is the process of constructing new basis vectors from old basis vectors, while backward transformation does the opposite, constructing old basis vectors from new ones.
- 📏 The script explains that tensors are invariant under a change of coordinate system, highlighting the importance of understanding transformations for working with tensors.
- 📝 The video provides a step-by-step example of how to perform forward and backward transformations in two-dimensional spaces using basis vectors E1, E2, E1 tilde, and E2 tilde.
- 🔢 The coefficients for constructing new basis vectors from old ones are arranged in a matrix called 'F' for forward transformation, and similarly, a matrix 'B' for backward transformation.
- 🧩 The arrangement of numbers in the forward and backward matrices is flipped about the main diagonal due to the chosen convention for matrix multiplication in the video series.
- ⚖️ The video demonstrates that multiplying the forward matrix 'F' by the backward matrix 'B' results in the identity matrix, proving that 'F' and 'B' are inverses of each other.
- 🔍 The script generalizes the concept of transformations to N dimensions, explaining how to construct new basis vectors from old ones using an N by N matrix of coefficients.
- 📉 The summation formulas provided in the script allow for a concise representation of the forward and backward transformations in N dimensions.
- 🔄 The Kronecker Delta, represented by the symbol 'δ', is introduced as a way to denote the entries of the identity matrix, where there is a one where the row equals the column and zeros elsewhere.
- 📚 The video concludes with a summary of the formulas for forward and backward transformations in N dimensions and the proof that these transformations are indeed inverses of each other.
Q & A
What is the main focus of this video in the series on tensors?
-The main focus of this video is to introduce the concepts of forward and backward transformations, which are the mathematical rules that allow movement between different coordinate systems.
Why is it important to understand transformations between coordinate systems when studying tensors?
-Understanding transformations between coordinate systems is important because tensors are invariant under a change of coordinate system, making this understanding crucial for a proper comprehension of tensors.
What does the forward transformation in the context of this video entail?
-The forward transformation involves moving from the old basis vectors to the new basis vectors by constructing the new basis vectors as linear combinations of the old basis vectors.
How are the new basis vectors represented in terms of the old basis vectors in the forward transformation?
-The new basis vectors are represented as linear combinations of the old basis vectors, with specific coefficients that determine the construction of the new basis from the old.
What is the significance of the matrix F in the forward transformation?
-Matrix F, which stands for 'forward', contains the coefficients that describe how the new basis vectors are constructed from the old basis vectors, and it is essential for understanding the forward transformation.
How is the arrangement of numbers in the forward matrix F related to the equations for the basis vectors?
-The numbers in matrix F are arranged in a way that is flipped about the main diagonal compared to the equations for the basis vectors, due to the convention of writing basis vectors in rows and multiplying from the left.
What is the purpose of the backward transformation?
-The purpose of the backward transformation is to construct the old basis vectors using the new basis vectors, essentially reversing the process of the forward transformation.
How is the backward transformation related to the forward transformation?
-The backward transformation is essentially the inverse of the forward transformation, and it can be represented by a matrix B, which is the inverse of matrix F.
What is the identity matrix, and why is it significant in the context of transformations?
-The identity matrix is a square matrix with ones along the main diagonal and zeros elsewhere. It is significant because when the forward and backward transformation matrices are multiplied, the result is the identity matrix, indicating that the transformations are indeed inverses of each other.
What is the Kronecker Delta symbol, and how is it used in the context of this video?
-The Kronecker Delta symbol, denoted by δ, is used to represent the behavior of having a value of one where the row index equals the column index and zero elsewhere, similar to the entries of the identity matrix.
How can the formulas for forward and backward transformations be generalized to N dimensions?
-The formulas for forward and backward transformations can be generalized to N dimensions by using an N by N matrix to represent the coefficients for constructing the new basis vectors from the old basis vectors, and vice versa.
What is the next topic that will be covered in the video series?
-The next topic in the video series will be vector components, which allow for the construction of generic vectors out of basis vectors, with the components typically written as column vectors that can be transformed using the forward and backward matrices.
Outlines
📚 Introduction to Tensor Transformations
This paragraph introduces the concept of tensor transformations, focusing on forward and backward transformations between different coordinate systems. The speaker explains that tensors remain invariant under changes in coordinate systems, emphasizing the importance of understanding these transformations. The forward transformation is described as a process of constructing new basis vectors from old ones using linear combinations. An example with two-dimensional coordinate systems is provided, where the new basis vectors E1 tilde and E2 tilde are expressed in terms of the old basis vectors E1 and E2. A forward transformation matrix 'F' is introduced, with its elements arranged to reflect the multiplication of basis vectors from the left by the matrix. The paragraph concludes with a brief mention of the backward transformation, which is the inverse process of constructing old basis vectors from new ones.
🔄 Detailed Explanation of Forward and Backward Transformations
This paragraph delves deeper into the mechanics of forward and backward transformations, using the example of two-dimensional coordinate systems. The forward transformation matrix 'F' is detailed, showing how the new basis vectors are formed from the old ones. The arrangement of the matrix elements is explained, with a focus on the row-by-column multiplication process. The backward transformation is then discussed, where the old basis vectors are constructed from the new basis vectors, and a backward transformation matrix 'B' is introduced. The speaker clarifies that 'B' is the inverse of 'F', and despite their functional similarity, different letters are used for visual distinction. The paragraph concludes with a matrix multiplication exercise that results in the identity matrix, confirming that 'F' and 'B' are indeed inverses.
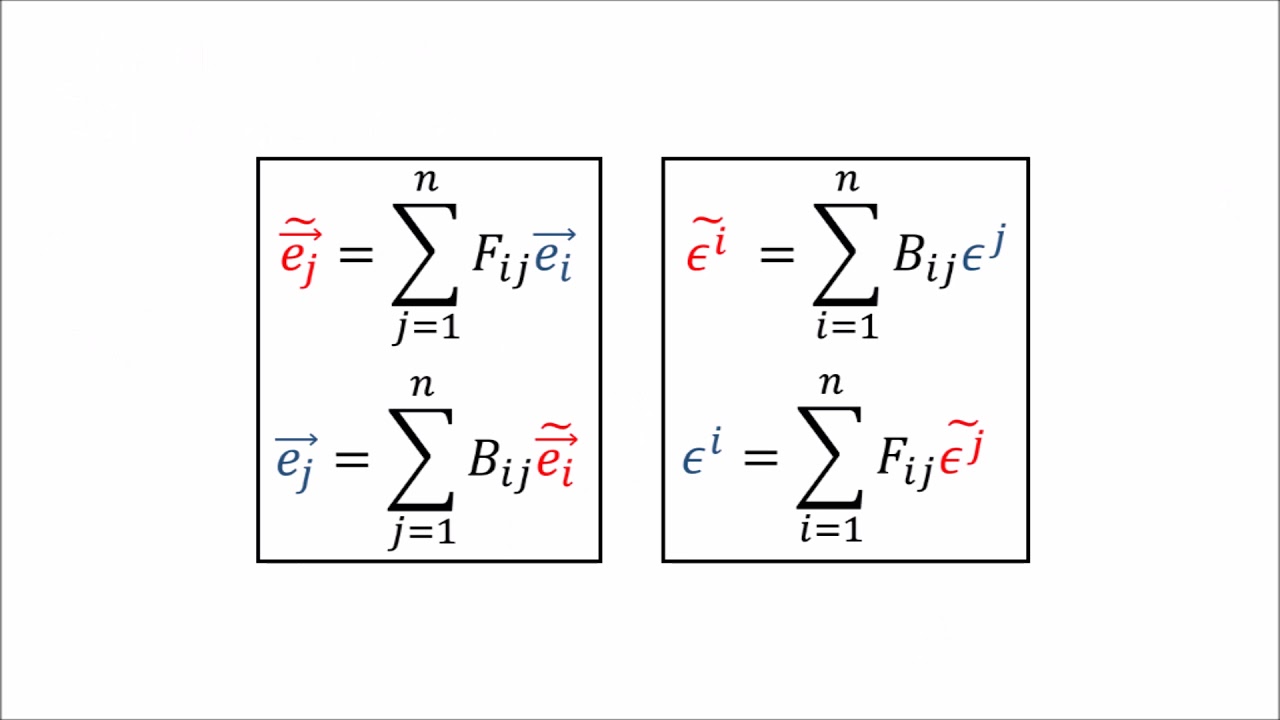
🔢 Generalizing Transformations to N Dimensions
The speaker extends the concept of transformations to N dimensions, explaining how to construct new basis vectors from old ones using appropriate coefficients. The forward transformation is represented by an N by N matrix 'F', and the backward transformation by an N by N matrix 'B'. The paragraph introduces summation notation to succinctly express the linear combinations of basis vectors for both transformations. The speaker also discusses the flexibility in relabeling summation indices and the commutativity of numerical coefficients in the summation. The paragraph concludes with a proof that the forward and backward transformations are inverses of each other, using the Kronecker Delta symbol to represent the identity matrix resulting from the multiplication of 'F' and 'B'.
🧩 Summarizing Tensor Transformations and Looking Ahead
In this concluding paragraph, the speaker summarizes the key points covered in the video: the formulas for forward and backward transformations in N dimensions and the demonstration that these transformations are inverses of each other, as evidenced by the identity matrix resulting from their multiplication. The speaker also introduces the Kronecker Delta symbol, which represents the entries of the identity matrix. The paragraph ends with a preview of the next topic to be covered in the series: vector components and their transformation using the forward and backward matrices.
Mindmap
Keywords
💡Tensors
💡Coordinate Systems
💡Basis Vectors
💡Forward Transformation
💡Backward Transformation
💡Matrix
💡Linear Combination
💡Inverse Matrices
💡Identity Matrix
💡Kronecker Delta
💡Vector Components
Highlights
Introduction to the concept of tensors and their importance in understanding transformations between different coordinate systems.
Explanation of forward and backward transformations as the rules for moving between coordinate systems.
Tensors are invariant under a coordinate system change, emphasizing their significance in mathematical physics.
Illustration of constructing new basis vectors from old basis vectors using linear combinations.
Introduction of the forward transformation matrix 'F' and its role in basis construction.
Clarification on the arrangement of basis vectors and matrix multiplication conventions used in the video series.
Demonstration of how to derive the backward transformation matrix 'B' from the new basis vectors.
Multiplication of forward and backward transformation matrices results in the identity matrix, indicating their inverse relationship.
Generalization of the transformation process to N dimensions, expanding the concepts from 2D to higher dimensions.
Introduction of the summation notation to simplify the representation of forward and backward transformations in N dimensions.
Explanation of the Kronecker Delta and its role in representing the identity matrix entries.
Proof that the forward and backward transformations are inverses by substituting and rearranging summation signs.
The importance of relabeling summation index letters without changing the formula's meaning for consistency.
The practical application of the Kronecker Delta in simplifying the representation of the identity matrix.
Summary of the video's content, including the formulas for forward and backward transformations and their inverse relationship.
Anticipation of the next video's content, which will focus on vector components and their transformation using the forward and backward matrices.
Transcripts
Browse More Related Video

Tensor Calculus 3: The Jacobian

Tensors for Beginners 2: Vector definition

Tensor Calculus 5: Derivative Transformation Rules (Contravariance)
Tensors for Beginners 6: Covector Transformation Rules

Tensors for Beginners 7: Linear Maps

Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra
5.0 / 5 (0 votes)
Thanks for rating: