Equation of Tangent Calculus Grade 12

Kevinmathscience
18 Sept 202004:22
EducationalLearning
32 Likes 10 Comments

TLDRThis video script explains the concept of finding the equation of a tangent to a graph by using the first derivative to determine the gradient. It illustrates that the tangent and the graph share the same gradient at the point of contact. The process involves calculating the first derivative of the graph's equation to find the gradient, then using the x-value of the point of tangency to find the y-value and subsequently the equation of the tangent line. An example is provided, demonstrating how to find the equation of a tangent to a cubic function when x equals three, resulting in the tangent equation y = 12x - 32.

Takeaways
  • 📈 The gradient of a graph can be found using the first derivative.
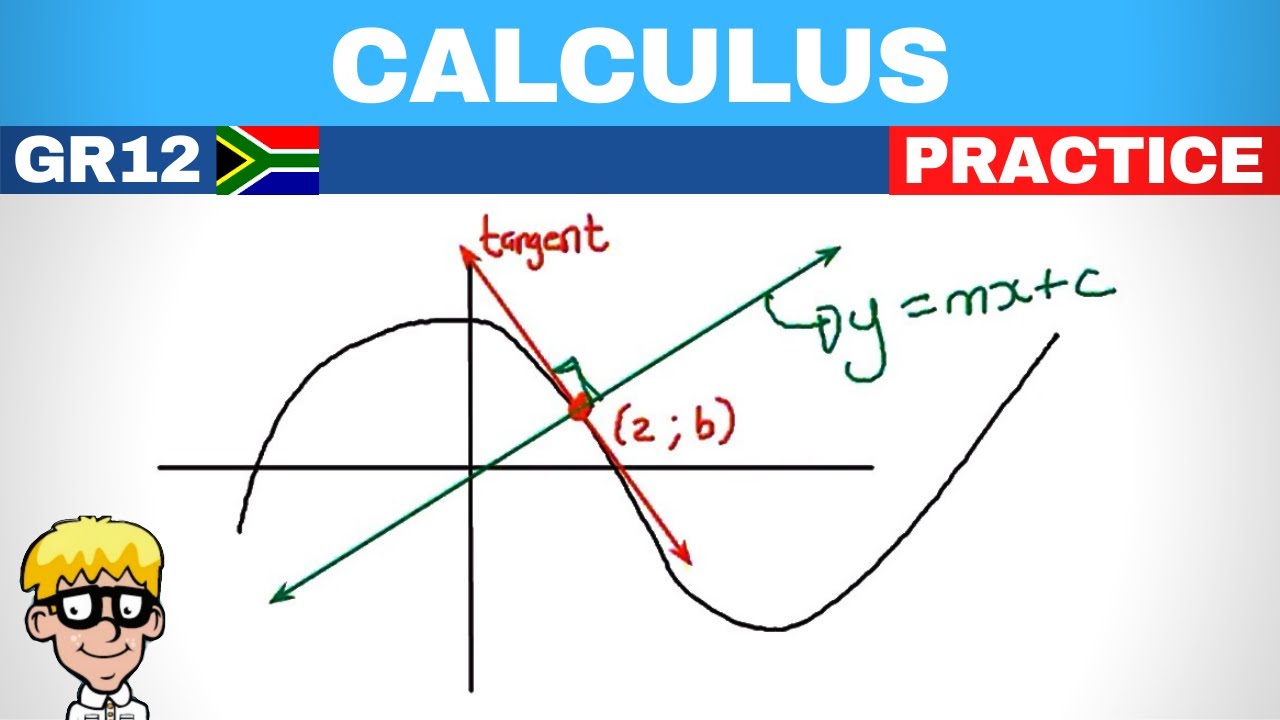
  • 📏 A tangent is a straight line that touches the graph at exactly one point.
  • 🔍 When zoomed in closely, the tangent and the graph have the same gradient at the point of contact.
  • 📘 The general equation of a tangent line is y = mx + c, where m is the gradient.
  • 🔑 To find the equation of the tangent line, you need the gradient and a point of contact.
  • 🔢 The gradient at a specific point on the graph can be calculated by substituting the x-value into the first derivative of the graph's equation.
  • 📝 To find the y-value for the point of contact, substitute the x-value into the original graph's equation.
  • 🧩 The coordinates of the point of contact are used to solve for 'c' in the tangent's equation.
  • 📚 An example is provided where the graph's equation is given as f(x) = x^3 - 2x^2 - 3x + 4, and the task is to find the tangent when x is 3.
  • 📉 The first derivative of the given graph's equation is 3x^2 - 4x - 3, which represents the gradient of the graph.
  • 📌 Substituting x = 3 into the first derivative gives a gradient of 12 for the tangent line.
  • 📐 Using the x and y values at the point of contact (3, 4), the equation of the tangent line is found to be y = 12x - 32.
Q & A

  • What is the relationship between the gradient of a graph and its tangent at a specific point?

    -The gradient of a graph at a specific point is equal to the gradient of the tangent line at that same point. This is because a tangent touches the graph at exactly one point and has the same slope as the graph at that point.

  • What is the general formula for a straight line, and what does 'm' represent in this formula?

    -The general formula for a straight line is y = mx + c, where 'm' represents the gradient or slope of the line.

  • How can you determine the equation of a tangent line to a graph at a given point?

    -To determine the equation of a tangent line, you need to know the gradient of the graph at the point of tangency and a point through which the tangent passes. The gradient can be found using the first derivative of the graph's equation, and the point can be found by substituting the x-value of the tangency point into the original graph's equation.

  • Why is it important to zoom in closely to the graph when considering the tangent?

    -Zooming in closely helps to visualize the point of tangency where the tangent and the graph have the same gradient. At this point, the graph and the tangent are almost indistinguishable and appear parallel.

  • What is the first step in finding the equation of a tangent line to a given graph?

    -The first step is to find the first derivative of the graph's equation, which gives you the gradient of the graph at any point.

  • How do you find the gradient of the graph at a specific x-value?

    -You substitute the x-value into the first derivative of the graph's equation to find the gradient at that specific point.

  • What is the purpose of finding the y-value at the point of tangency?

    -The y-value at the point of tangency, along with the x-value, is used to find the constant 'c' in the equation of the tangent line (y = mx + c).

  • Can you find the equation of a tangent line without knowing the y-value at the point of tangency?

    -No, you need both the x and y values at the point of tangency to determine the full equation of the tangent line.

  • What is the equation of the tangent line if the gradient is 12 and the point of tangency is (3, 4)?

    -The equation of the tangent line is y = 12x + c. To find 'c', substitute the x and y values of the point of tangency into the equation and solve for c.

  • In the provided example, what is the original equation of the graph?

    -The original equation of the graph is f(x) = x^3 - 2x^2 - 3x + 4.

  • How do you find the value of 'c' in the equation of the tangent line using the point of tangency?

    -Substitute the x and y values of the point of tangency into the equation y = mx + c and solve for c. In the example, with m = 12, x = 3, and y = 4, you would get c = 4 - (12 * 3) = -32.

Outlines
00:00
📈 Understanding Tangent Gradients

This paragraph explains the concept of the gradient of a graph and how it can be determined using the first derivative. It introduces the idea of a tangent line touching the graph at a single point and having the same gradient as the graph at that point. The general formula for a straight line, y = mx + c, is discussed, where 'm' represents the gradient. The paragraph further illustrates the process of finding the equation of a tangent line by using the gradient at a specific point on the graph and the coordinates of the point of contact. An example problem is presented, where the equation of a graph is given, and the task is to find the equation of the tangent at a particular x-value.

Mindmap
Keywords
💡Gradient
The gradient, in the context of this video, refers to the slope or steepness of a graph, which indicates the rate of change of a function at a given point. It is a fundamental concept in calculus and is used to determine the direction and steepness of a tangent line to the graph. In the script, the gradient is obtained by calculating the first derivative of the function, which is essential for finding the equation of the tangent line at a specific point on the graph.
💡Tangent
A tangent is a straight line that touches the graph of a function at a single point without crossing it. It is parallel to the graph at that point and has the same slope or gradient. The concept of a tangent is central to the video's theme, as it is used to illustrate how the equation of a tangent line can be derived from the graph of a function, specifically by using the first derivative at the point of tangency.
💡First Derivative
The first derivative of a function is a measure of its instantaneous rate of change at any given point. In the video, the first derivative is used to find the gradient of the graph at a specific point, which is then used to determine the slope of the tangent line. The first derivative is calculated by differentiating the original function, and it is crucial for understanding the behavior of the graph at any point.
💡Equation of a Tangent
The equation of a tangent is a linear equation that represents the tangent line to a curve at a specific point. In the video, the general form of this equation is given as y = mx + c, where m is the gradient (slope) and c is the y-intercept. The script explains how to derive this equation by using the first derivative of the graph's equation and a known point of tangency.
💡Graph
A graph is a visual representation of the relationship between two variables, typically plotted on a coordinate plane. In the video, the graph represents the function whose behavior is being analyzed. The script discusses how the gradient of the graph at a specific point can be determined and how a tangent line can be drawn at that point.
💡Point of Contact
The point of contact is the specific location on the graph where the tangent line touches the curve. It is a critical concept in the video because it is the point at which the gradient of the graph and the tangent are equal. The script uses this concept to explain how to find the coordinates of the point of tangency and to determine the equation of the tangent line.
💡Slope
Slope is another term for the gradient or steepness of a line, indicating how much the line rises or falls for a given horizontal distance. In the video, the slope is discussed in the context of the tangent line's equation, where it is represented by the variable 'm' in the formula y = mx + c.
💡Parallel
Parallel lines are lines that never intersect and have the same slope or gradient. In the script, the concept of parallelism is used to describe the relationship between the tangent line and the graph at the point of contact, emphasizing that they have the same slope at that specific point.
💡X and Y Values
X and Y values are the coordinates of a point on a graph. In the video, the script explains how to find the x and y values at the point of contact between the graph and the tangent line. These values are essential for determining the equation of the tangent line by substituting them into the graph's equation and the tangent's equation.
💡Substitution
Substitution is a method used in algebra to solve for an unknown variable by replacing it with an expression or value. In the context of the video, substitution is used to find the value of 'c' in the tangent's equation by plugging in the known x and y values of the point of contact.
💡Example
An example in the video is a specific case used to illustrate the process of finding the equation of a tangent line. The script provides a detailed example involving the function f(x) = x^3 - 2x^2 - 3x + 4, where the equation of the tangent line when x is 3 is determined by following the steps explained in the video.
Highlights

The gradient of a graph can be obtained by using the first derivative.

A tangent is a straight line that touches the graph at one point.

The equation of a tangent line is y = mx + c, where m is the gradient.

At the point of contact, the tangent and the graph have the same gradient.

To find the gradient of the graph, use the x value and the first derivative.

If the gradient at a point is known, substitute it into the tangent equation 2x + c.

To find c, substitute the x and y values at the point of contact.

At the point of contact, the tangent and graph share the same x and y values.

Plug the x value from the point of contact into the graph's equation to find the y value.

Substitute the x and y values into the tangent equation to solve for c.

An example is given with the graph equation f(x) = x^3 - 2x^2 - 3x + 4.

The task is to determine the equation of the tangent when x is 3.

The gradient of the tangent is the same as the gradient of the graph at the point of contact.

The first derivative of the graph's equation is 3x^2 - 4x - 3.

Substitute x = 3 into the derivative to find the gradient of the graph at that point, which is 12.

The coordinates of the point of contact are (3, 4).

Plug the coordinates (3, 4) into the tangent equation to find c = -32.

The equation of the tangent is y = 12x - 32.

Transcripts

Browse More Related Video

Calculus Grade 12: Tangent

Equation of a tangent line [IB Maths AI SL/HL]

Calculus Grade 12 Tangent

Implicit Differentiation - Finding Equation of Tangent Line

Calculus grade 12: Exam

Equation of a normal line [IB Maths AI SL/HL]

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Graph AnalysisTangent LineDerivativeGradientEquationCalculusMathematicsEducationalTutorialFirst DerivativeGraphing