Calculus grade 12: Exam

Kevinmathscience

21 May 202213:48

EducationalLearning

32 Likes 10 Comments

TLDRThis video script discusses a cubic graph with specific characteristics, including a y-intercept and x-coordinates of turning points. It explains how to determine when the graph increases, identifies the x-coordinate of inflection points, and clarifies when the graph is concave up or down. The script also guides viewers through finding the equation of a cubic function from its derivative and determining the equation of the tangent with the maximum gradient at the inflection point, providing a comprehensive overview of calculus concepts.

Takeaways

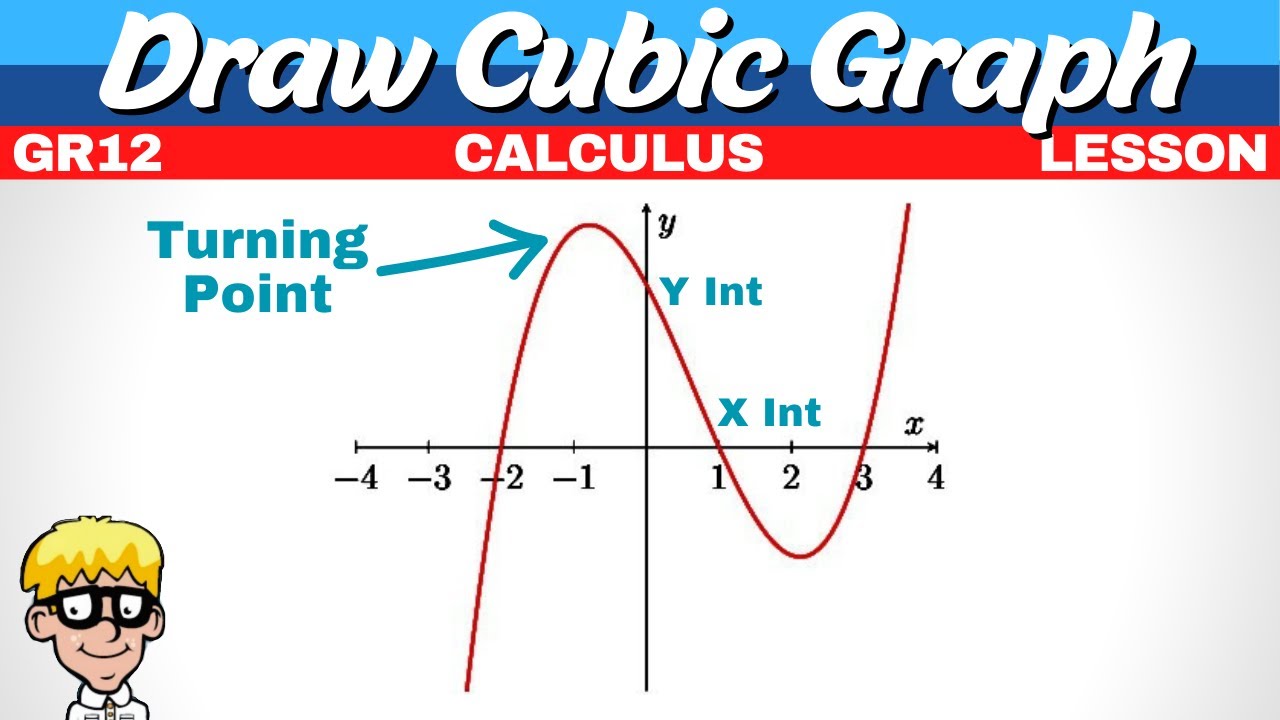
📈 The cubic graph has a y-intercept, and its turning points have x-coordinates of -1 and 2.
🆙 The graph increases when x is greater than -1 and less than 2.
🔄 The x-coordinate of the point of inflection is found by averaging the x-coordinates of the turning points, resulting in x = 0.5.
⬇️ The graph is concave down when x is greater than 0.5.
🔢 Concave down and concave up are related to the sign of the second derivative; concave down when the second derivative is negative and concave up when it's positive.
🧮 The first derivative of the function is given, and by matching coefficients, the original function g(x) is determined.
📏 A tangent to the graph has the same gradient as the graph at the point of contact.
🔍 To find the equation of the tangent with the maximum gradient, the gradient at the inflection point (x = 0.5) is calculated.
💡 The gradient of the tangent at the inflection point is found to be 13.5, and the equation of the tangent line is determined.
📝 The final equation of the tangent with the maximum gradient is y = 13.5x - 0.25.

Q & A

What is the y-intercept and the x-coordinates of the turning points mentioned in the graph?
-The y-intercept and the x-coordinates of the turning points on the graph are given as -1 and 2.
For which values of x will the graph increase?
-The graph increases for values of x greater than -1 and less than 2.
What is the inflection point, and how is it determined?
-The inflection point is the point where the graph changes from concave up to concave down or vice versa. It is found by calculating the midpoint between the turning points, which in this case is (−1 + 2)/2 = 0.5.
How do you identify the regions where the graph is concave down?
-The graph is concave down for values of x greater than 0.5. This is determined by examining the second derivative, which is negative in this region.
What does it mean for a graph to be concave down or concave up?
-Concave down means the graph opens downward (like an upside-down parabola), and concave up means the graph opens upward. Concave down occurs where the second derivative is negative, and concave up occurs where the second derivative is positive.
How do you determine the equation of the original function g(x) given its first derivative?
-The equation of g(x) is found by integrating the first derivative, which in this case involves solving for constants using given conditions. The final equation is g(x) = -2x^3 + 3x^2 + 12x.
What is the significance of the inflection point in determining the maximum gradient of a tangent?
-The inflection point is significant because it represents the point on the graph where the gradient is the steepest, meaning it has the maximum gradient for a tangent.
How is the equation of the tangent with the maximum gradient determined?
-The equation of the tangent with the maximum gradient is determined by finding the gradient at the inflection point (using the first derivative) and then using this gradient to form the tangent equation. The final equation is y = 13.5x - 0.25.
What is the relationship between the gradient of the tangent and the gradient of the graph?
-The gradient of the tangent at any point on the graph is equal to the gradient of the graph at that point, which is found using the first derivative of the function.
Why is the inflection point considered the steepest place on the graph?
-The inflection point is considered the steepest place on the graph because it is where the change from concave up to concave down occurs, resulting in the maximum possible gradient for the tangent at that point.

Outlines

00:00

📈 Understanding the Graph's Increase

This paragraph discusses the conditions under which a cubic graph increases. The speaker explains that the graph increases between the x-coordinates of -1 and 2, and this is represented in interval notation as (-1, 2). The explanation is clear and concise, emphasizing the significance of identifying the intervals where the graph rises.

05:02

🔄 Identifying the Point of Inflection

The speaker describes how to find the x-coordinate of the inflection point on a cubic graph. An inflection point is where the concavity changes, and it lies midway between the turning points. By calculating the midpoint between -1 and 2, the x-coordinate of the inflection point is determined to be 0.5. The explanation includes a brief overview of the second derivative but focuses on the midpoint calculation for simplicity.

10:04

📉 Determining Where the Graph is Concave Down

This paragraph explains how to determine the x-values where the graph is concave down. Concavity is discussed with a brief comparison between concave down and concave up regions. The speaker highlights that the graph is concave down for x-values greater than 0.5, and this interval is from 0.5 to infinity. The inflection point is noted as the boundary where concavity changes.

🔄 Working Backwards to Determine the Original Equation

The speaker introduces the concept of working backwards from the derivative of a cubic function to determine the original equation of the function. By matching the coefficients of the given derivative with the corresponding terms of the general cubic function, the speaker derives the values of constants a, b, and c. These constants are then used to construct the original cubic equation. This section highlights the importance of understanding the relationship between a function and its derivative.

📏 Finding the Tangent with Maximum Gradient

This section focuses on determining the equation of the tangent to the graph at the point where the gradient is maximized. The speaker identifies the inflection point as the location where the gradient is steepest. By substituting the inflection point's x-coordinate into the derivative, the gradient is calculated. The speaker then finds the equation of the tangent line by substituting the gradient and coordinates of the inflection point into the linear equation format. The result is a clear step-by-step process to derive the equation of the tangent with the maximum gradient.

Mindmap

Keywords

💡Cubic Graph

A cubic graph in the context of the video refers to a graph of a cubic function, which is a polynomial of degree three. The script discusses the characteristics of such a graph, including its turning points and the intervals over which the graph increases or decreases. The cubic graph is central to the video's theme of understanding the behavior of cubic functions.

💡Y-intercept

The y-intercept is the point where a graph crosses the y-axis. In the video, the y-intercept is mentioned in relation to the cubic graph, indicating a specific value at which the function intersects the y-axis, which is a key feature in graphing and analyzing the function's behavior.

💡Turning Point

A turning point on a graph is where the concavity changes, indicating the maximum or minimum points of the graph. The script identifies the x-coordinates of the turning points as -1 and 2, which are critical in determining the intervals of increase and decrease on the cubic graph.

💡Interval Notation

Interval notation is a way of expressing a set of real numbers between two endpoints. The video uses interval notation to describe the x-values for which the graph of the cubic function is increasing, enhancing the viewer's understanding of the function's behavior over specific ranges.

💡Inflection Point

An inflection point is a point on the graph where the concavity changes. The script explains that the inflection point is in the middle of the turning points and is where the second derivative is zero. It is a key concept in the video as it helps determine the concavity of the cubic graph.

💡Concave Down/Up

Concave down and concave up describe the curvature of a graph. A graph is concave down where it curves downwards like a U-shape, and concave up where it curves upwards. The video explains these concepts to identify the regions of the cubic graph where the function is bending in these ways, which is crucial for understanding the graph's shape.

💡Second Derivative

The second derivative of a function measures how the rate of change of the first derivative is itself changing. In the video, the second derivative is discussed in the context of determining concavity and identifying the inflection point, which is where the second derivative is zero.

💡Integration

Integration is a mathematical process that is the reverse of differentiation and can be used to find the original function given its derivative. The script mentions integration as a technique for finding the equation of a function, though it notes that not all viewers may be familiar with the concept.

💡Gradient

In the context of the video, the gradient refers to the slope or steepness of a line, which is synonymous with the first derivative of a function. The script discusses finding the gradient of the cubic function at specific points, particularly at the inflection point, to determine the equation of a tangent line.

💡Tangent

A tangent to a curve at a given point is a straight line that touches the curve at that point without crossing it. The video asks viewers to find the equation of the tangent with the maximum gradient, which is related to the steepest part of the curve, indicating the inflection point.

💡Equation of a Tangent

The equation of a tangent to a curve at a specific point can be written in the form y = mx + c, where m is the gradient (slope) and c is a constant. The video demonstrates how to find this equation by using the gradient at the inflection point and a known point on the curve to solve for c.

Highlights

Explanation of the graph's increasing intervals: The graph increases when x is greater than -1 and less than 2.

Introduction to the concept of an inflection point: It occurs in the middle of the turning points and is where the second derivative equals zero.

Calculation of the inflection point: Found by taking the average of the turning points (-1 and 2), resulting in an x-coordinate of 0.5.

Explanation of concave down and concave up: Concave down is when the second derivative is negative, and concave up is when it is positive.

Identification of the concave down interval: The graph is concave down when x is greater than 0.5.

Derivation of the equation of g(x): Given the first derivative, the equation of g(x) is determined as -2x³ + 3x² + 12x.

Explanation of a tangent to a curve: A tangent touches the curve at exactly one point, and its gradient is the same as the gradient of the curve at that point.

Finding the tangent with the maximum gradient: The steepest tangent is found at the inflection point, which is the point of maximum steepness on the curve.

Calculation of the gradient at the inflection point: Using the first derivative, the gradient at x = 0.5 is found to be 13.5.

Formulation of the tangent's equation: The equation of the tangent at the inflection point is y = 13.5x - 0.25.

Understanding the significance of the inflection point: It is not only where the concavity changes but also where the graph has the steepest tangent.

Utilization of basic calculus concepts: The process includes using derivatives to find critical points, concavity, and the equation of tangents.

Link between the first derivative and gradient: The first derivative is directly related to the gradient of the curve.

Introduction of the concept of integration: Mentioned as an advanced method for finding the original function from its derivative, though not necessary for this problem.

Importance of precise calculation: The process emphasizes careful calculation, particularly when determining the values for the gradient and tangent equation.

Transcripts

Browse More Related Video

Calculus grade 12: Practice

Calculus Grade 12 Exam Questions

Draw Cubic Graph Grade 12

Calculus Grade 12: Tangent

Inflection Point Grade 12