Calculus Grade 12: Tangent
TLDRThe video explains the process of finding the equation of a tangent to a cubic graph at a specific point using calculus. It highlights the importance of understanding that the gradient of the tangent is equal to the gradient of the graph at the point of contact. The speaker walks through the steps of deriving the gradient using the first derivative and finding the y-intercept by substituting the x-value into the original equation. The final result is the equation of the tangent line.
Takeaways
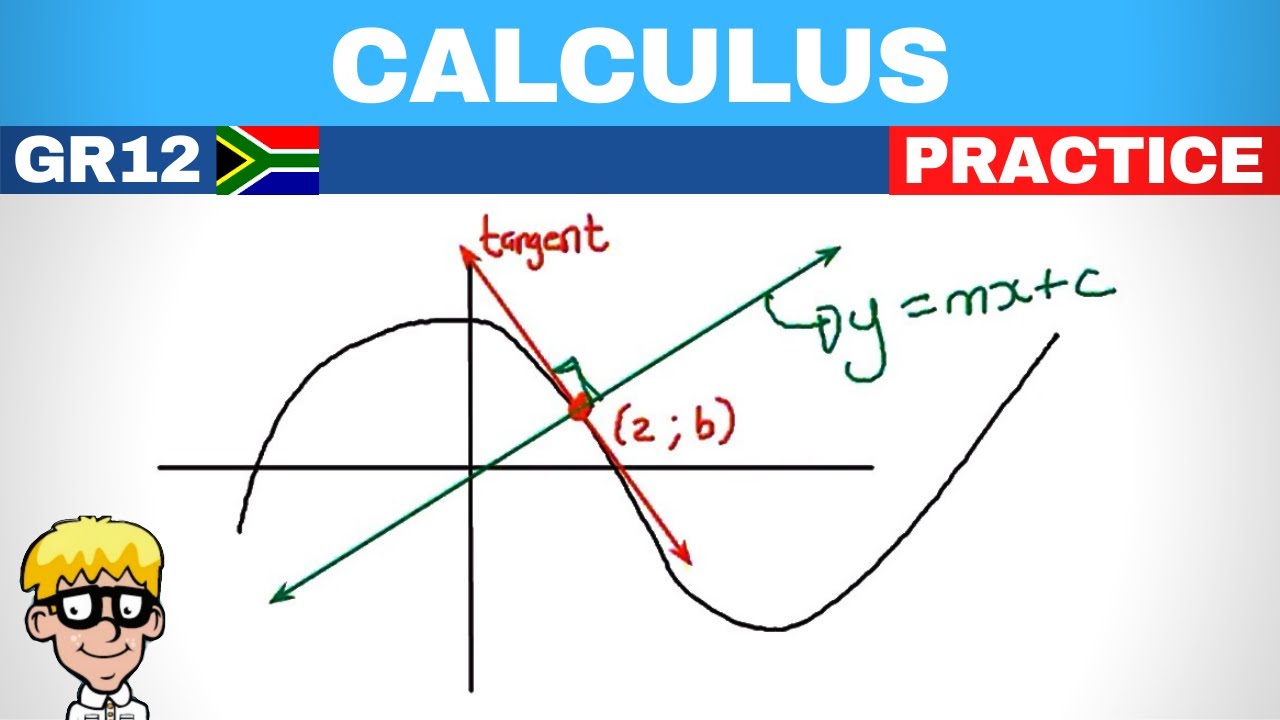
- 📈 The script discusses a cubic graph and its tangent line, emphasizing the relationship between the gradient of the graph and the tangent at a specific point.
- 🔍 It is important to understand that the tangent line is a straight line and its general equation is y = mx + c, where m represents the gradient.
- 📌 The gradient of the tangent at a point of contact is equal to the gradient of the graph at that point, which is a critical concept for solving the problem.
- 🧭 To find the gradient of the graph, calculus is used, specifically the first derivative of the function, which in the script's example is 3x^2 - 6x - 6.
- ❌ The script clarifies that the first derivative should not be set to zero as it would imply the gradient is zero, which is not the case here.
- 📍 The x-value of the point of tangency is given as 2, which is used to find the gradient of the graph at that specific point.
- 📉 By substituting x = 2 into the derivative, the gradient of the graph at that point is found to be -6, which is also the gradient of the tangent line.
- 🔢 The script demonstrates how to find the y-value of the point of tangency by substituting x = 2 into the original cubic equation, resulting in y = -24.
- 📝 The point (2, -24) lies on both the graph and the tangent line, which is used to find the y-intercept 'c' of the tangent line's equation.
- 🔄 The equation of the tangent line is derived by using the point (2, -24) and the gradient -6, resulting in y = -6x - 12.
- 💡 The script serves as an example to illustrate the process of finding the equation of a tangent line to a cubic graph at a given point.
Q & A
What is the general equation of a tangent line?
-The general equation of a tangent line is y = mx + c, where m is the gradient (slope) and c is the y-intercept.
Why is the gradient of a tangent line equal to the gradient of the graph at the point of tangency?
-The gradient of a tangent line is equal to the gradient of the graph at the point of tangency because a tangent touches the graph at exactly one point, and at that point, the slope of the tangent line matches the slope of the graph.
What mathematical concept is used to find the gradient of a graph?
-The mathematical concept used to find the gradient of a graph is the first derivative in calculus, which represents the rate of change of the function at any given point.
What is the first derivative of the given cubic function 3x^2 - 6x - 6?
-The first derivative of the cubic function 3x^2 - 6x - 6 is 6x - 6.
Why is the first derivative not set to zero in this context?
-The first derivative is not set to zero because we are not looking for stationary points but rather the gradient at a specific point x = 2, which is not necessarily a point where the gradient is zero.
What is the gradient of the graph when x is 2?
-When x is 2, the gradient of the graph is -6, as found by substituting x = 2 into the first derivative 6x - 6.
How do you find the y-value of the point of tangency without knowing it initially?
-You can find the y-value of the point of tangency by substituting the known x-value into the original equation of the graph, which gives you the corresponding y-value.
What is the y-value of the point of tangency when x is 2 for the given graph?
-The y-value of the point of tangency when x is 2 is -24, obtained by substituting x = 2 into the original cubic equation 3x^2 - 6x - 6.
How is the y-intercept (c) of the tangent line found?
-The y-intercept (c) of the tangent line is found by using the point-slope form of the line equation and substituting the known x and y values of the point of tangency.
What is the equation of the tangent line to the graph at x = 2?
-The equation of the tangent line to the graph at x = 2 is y = -6x - 12, found by using the gradient -6 and the point (2, -24).
Why might the gradient of the tangent line appear to be positive in some examples?
-The gradient of the tangent line might appear to be positive in some examples due to the orientation or the specific view of the graph, but the actual gradient at the point of tangency is determined by the first derivative of the original function at that point.
Outlines
📈 Understanding Tangents and Gradients in a Cubic Graph
This paragraph explains the concept of a tangent line on a cubic graph. It discusses how a tangent line, which is a straight line, has a general equation of y = mx + c, where m represents the gradient. The key point emphasized is that the gradient of the tangent at a specific point is the same as the gradient of the graph at that point. The paragraph also introduces the importance of finding the gradient of the graph at a given point using the first derivative in calculus.
🔍 Calculating the Gradient of the Tangent
This section details the process of finding the gradient of a tangent line at a specific point on a cubic graph. The first derivative of the graph's equation is used to determine the gradient. By substituting the x-value of 2 into the derivative, the gradient is calculated to be -6. Although the visual example might suggest a positive gradient, the explanation clarifies that the gradient is negative, based on the specific calculations for this scenario.
📊 Determining the Y-Value and the Tangent Line Equation
Here, the focus shifts to finding the y-value at the point where x equals 2 on the graph. By substituting x = 2 into the original cubic equation, the y-value is found to be -24. This point (2, -24) lies on both the graph and the tangent line. The paragraph then outlines the process of finding the c-value in the tangent's equation using this point, ultimately arriving at the equation of the tangent line: y = -6x - 12.
Mindmap
Keywords
💡Graph
💡Cubic Graph
💡Tangent
💡Gradient
💡First Derivative
💡Equation of a Line
💡X-Value
💡Y-Value
💡Point
💡Instantaneous Rate of Change
Highlights
Understanding the concept of a tangent to a cubic graph and its shape.
The general equation of a tangent line is y = mx + c, where m is the gradient.
The gradient of a tangent line is equal to the gradient of the graph at the point of tangency.
The goal is to find the gradient of the graph at a specific point.
Using calculus to find the gradient by taking the first derivative of the graph's equation.
The first derivative of the given cubic equation is 3x^2 - 6x - 6.
The x-value of the point of tangency is given as 2.
Substituting x = 2 into the derivative to find the gradient at that point.
The gradient of the graph when x is 2 is found to be -6.
The gradient of the tangent line is also -6, matching the graph's gradient at the point of tangency.
Finding the y-value of the point of tangency by substituting x = 2 into the original equation.
The y-value at x = 2 is calculated to be -24.
Using the point (2, -24) to help find the y-intercept 'c' of the tangent line.
Solving for 'c' in the equation y = -6x + c using the point (2, -24).
The y-intercept 'c' is found to be -12.
The final equation of the tangent line is y = -6x - 12.
The importance of understanding the relationship between the graph's gradient and the tangent's gradient.
The practical application of calculus in determining the equation of a tangent line.
The process of finding the y-intercept 'c' by using a known point on the graph and the tangent line.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: