Waves part 2 (Double Slit, Single Slit, and Standing Waves)
TLDRThis script delves into the phenomenon of double-slit interference, explaining how light waves from two slits create alternating bright and dark spots on a screen due to constructive and destructive interference. It discusses the path length difference formula, \( D \sin \theta = n\Lambda \), for determining these points. The script also explores single-slit interference and standing waves, including their wavelengths and frequencies, with a focus on node-node and node-antinode configurations. It concludes with the general formula for wavelengths and frequencies of harmonics in standing waves.
Takeaways
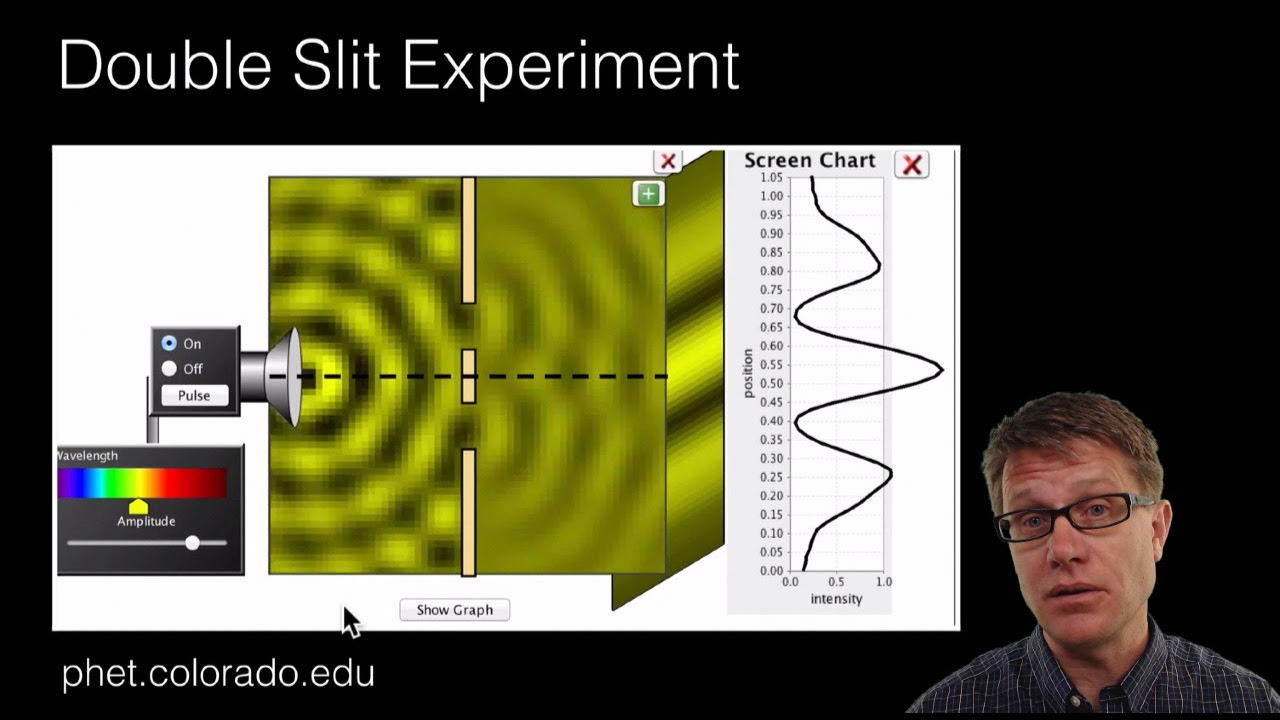
- 🔦 Two slits in a barrier create an interference pattern when light of wavelength Lambda is shot at the barrier.
- 🌊 Each slit acts as its own source of waves, causing overlapping waves that lead to interference.
- 🔆 Constructive interference occurs when the path length differences are whole numbers of wavelengths.
- 🌑 Destructive interference happens when path length differences are half numbers of wavelengths.
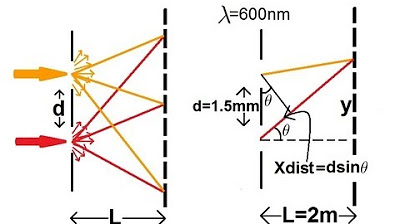
- 📐 The path length difference in double slit problems is D sin Theta, where D is the distance between the slits and Theta is the angle to a point on the screen.
- 🖥️ Constructive points on the screen are found where D sin Theta equals n Lambda (n is an integer).
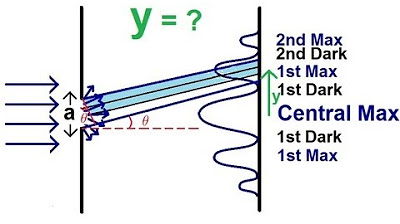
- 🎞️ Single slit interference also produces an interference pattern, with the central point being constructive.
- 🔍 For single slit interference, the formula D sin Theta = n Lambda determines destructive points.
- 🎹 Standing waves occur when a wave bounces back and forth between fixed distances, creating nodes and antinodes.
- 🔗 The fundamental wavelength of a standing wave is 2 * L, and the nth harmonic wavelength is given by Lambda = 2 L / n.
Q & A
What creates the interference pattern in a double slit experiment?
-The interference pattern in a double slit experiment is created by the overlap of waves from two slits, which can interfere constructively or destructively on a screen placed behind the slits.
How can you predict the points of constructive and destructive interference in a double slit experiment?
-You can predict the points of constructive and destructive interference by knowing that path length differences equal to whole numbers of wavelengths result in constructive interference, while path length differences equal to half numbers of wavelengths result in destructive interference.
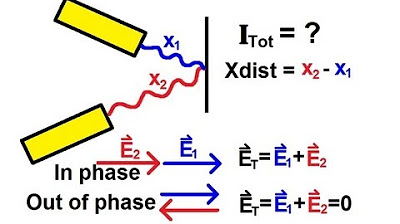
What does the path length difference refer to in a double slit experiment?
-In a double slit experiment, the path length difference refers to the difference between the distance that the wave from one slit travels to reach a point on the screen and the distance that the wave from the other slit travels to reach that same point.
How is the path length difference calculated in a double slit experiment?
-The path length difference in a double slit experiment is calculated using the formula D sin Θ, where D is the distance between the two slits and Θ is the angle to a point on the screen measured from the center line.
What is the condition for constructive interference in a double slit experiment?
-The condition for constructive interference in a double slit experiment is that D sin Θ must equal an integer number of wavelengths (D sin Θ = nλ).
What is the difference in the interference pattern when light shines on a single slit compared to a double slit?
-In a single slit experiment, the interference pattern also has alternating constructive and destructive points, but the formula D sin Θ = nλ now gives the condition for destructive points instead of constructive points, except for the center point, which remains constructive.
How does the brightness of the central constructive point compare between single slit and double slit interference?
-In single slit interference, the central constructive point has a much larger relative brightness compared to the other constructive points to the side of it, unlike in double slit interference.
What are standing waves and how are they formed?
-Standing waves occur when a wave is required to bounce back and forth between a fixed distance L, with nodes at the end points where no variation occurs. These waves are formed by the interference of the reflected waves.
What is the fundamental wavelength in a standing wave, and how is it calculated?
-The fundamental wavelength in a standing wave is the largest possible wavelength and is calculated as 2L, where L is the fixed distance between the endpoints.
How do you find the frequency of the nth harmonic in a standing wave?
-The frequency of the nth harmonic in a standing wave is found using the formula frequency = velocity / wavelength. The frequency of the nth harmonic is n times the fundamental frequency, where the fundamental frequency is velocity divided by twice the length (V/2L).
How do standing waves in a tube open at both ends differ from those in a tube open at one end?
-In a tube open at both ends, the standing wave has nodes at both ends and follows the same wavelength and frequency formulas as node-node standing waves. In a tube open at one end and closed at the other, the open end is a node and the closed end is an anti-node. The fundamental wavelength is 4L and subsequent wavelengths follow the formula 4L/(2n-1).
Outlines
🔬 Double Slit Interference Explained
In double slit interference, light of wavelength λ passes through two slits cut a distance D apart, creating two wave sources. These waves overlap, producing an interference pattern with alternating bright and dark spots on a screen. The points of constructive interference, where path length differences equal whole wavelengths, and destructive interference, where differences equal half wavelengths, can be predicted. The path length difference, D sin θ, determines the interference type. In a single slit, the central bright spot is more intense, and D sin θ = nλ marks destructive points.
🔊 Standing Waves and Harmonics
Standing waves form when a wave reflects back and forth between two fixed points, creating nodes (no movement) and antinodes (maximum displacement). The fundamental wavelength (λ) is 2L, with harmonics at λ = 2L/n. For example, the second harmonic has λ = L. Frequencies of these harmonics are multiples of the fundamental frequency. In a tube open at both ends, standing waves match those of a string. If one end is closed, the first wavelength is 4L, producing odd harmonics. The speed of sound, about 340 m/s, determines these frequencies.
Mindmap
Keywords
💡Double Slit Interference
💡Wavelength
💡Path Length Difference
💡Constructive Interference
💡Destructive Interference
💡Standing Waves
💡Fundamental Wavelength
💡Harmonics
💡Nodes
💡Antinodes
💡Frequency
Highlights
Double-slit interference involves light passing through two slits and creating an interference pattern on a screen.
Each slit acts as a wave source, leading to constructive or destructive interference.
Constructive interference occurs at points where path length differences are whole number multiples of the wavelength.
Destructive interference happens when path length differences equal half the wavelength multiplied by an integer.
Path length difference is the distance from one slit to a screen point minus the distance from the other slit to the same point.
The formula for path length difference in a double-slit experiment is D sin Theta, where D is the slit separation and Theta is the angle to the screen point.
For constructive points on the screen, D sin Theta equals n Lambda, with n being an integer and Lambda the wavelength.
Single-slit interference differs from double-slit, with the formula D sin Theta now representing destructive points except for the central constructive point.
The central constructive point in single-slit interference is significantly brighter than the others due to the lack of destructive interference.
Standing waves are formed when a wave oscillates between two fixed points, with nodes at the endpoints and antinodes at the maximum displacement points.
The fundamental wavelength in a standing wave is twice the distance between the fixed points, L.
Higher harmonics of standing waves have wavelengths given by Lambda = 2 L / n, where n is the harmonic number.
The frequency of the nth harmonic is n times the fundamental frequency.
For a tube open at both ends, the standing wave is a node-node standing wave with identical wavelengths and frequencies to the closed tube scenario.
A tube closed at one end and open at the other results in a node-antinode standing wave, with different fundamental wavelengths and frequencies.
The fundamental frequency of a node-antinode standing wave can be calculated using the speed of sound and the tube length.
The general formula for wavelengths in a node-antinode standing wave is 4 L / (2n - 1), where n is the harmonic number.
Frequencies of standing waves with a node at one end and an antinode at the other can be found using the speed of sound and the general wavelength formula.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: