Physics 60 Interference of Light (4 of 8) Young's Double Slit

Michel van Biezen
14 May 201314:01
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the fascinating phenomenon of light interference, specifically through Young's double-slit experiment. It explains how light waves passing through two closely spaced slits create an interference pattern on a distant screen, characterized by alternating bright and dark fringes. The script explores the principles behind constructive and destructive interference, and how the path length difference between the waves determines these patterns. It further illustrates the mathematical relationship between the fringe positions, the wavelength of light, the distance between slits, and the screen distance, providing a formula to calculate the positions of the maxima and minima in the interference pattern.

Takeaways
  • πŸ”¬ Young's double slit experiment demonstrates light interference patterns.
  • 🌈 Two small slits a distance D apart create interference when light passes through them.
  • πŸ“ The slits are very close together, typically within a fraction of a millimeter.
  • πŸ” Light diffracts through the slits, causing it to spread out in different directions.
  • ✨ An interference pattern of bright and dark fringes appears on a screen placed a few meters away.
  • πŸŽ› Constructive interference occurs where the path length difference is an integer multiple of the wavelength.
  • πŸ›‘ Destructive interference occurs where the path length difference is a half-integer multiple of the wavelength.
  • πŸ“ The position of bright and dark fringes can be calculated using the distance D, the wavelength Ξ», and the distance to the screen L.
  • 🌟 The central maximum is the brightest spot directly across from the slits.
  • πŸ“Š The distance of the fringes from the central maximum can be calculated using the formula y = (Ξ» * L) / D for bright fringes.
Q & A

  • What is the phenomenon described in the script?

    -The script describes the phenomenon of light interference, specifically using the example of Young's double-slit experiment.

  • What causes light to diffract when it passes through two closely spaced slits?

    -Light diffracts because the wavelength of the light is somewhat proportional to the size of the slits, causing the light to bend and spread out in different directions after passing through the slits.

  • What is an interference pattern in the context of Young's double-slit experiment?

    -An interference pattern refers to the alternating bright and dark regions observed on a screen some distance away from the slits, resulting from the constructive and destructive interference of light waves.

  • What is meant by constructive interference in the script?

    -Constructive interference occurs when the path length difference between the light waves from the two slits is an integer multiple of the wavelength, resulting in bright spots on the screen.

  • What is meant by destructive interference?

    -Destructive interference occurs when the path length difference is an odd multiple of half the wavelength, leading to dark spots on the screen where the light waves cancel each other out.

  • What is the central maximum in the context of the interference pattern?

    -The central maximum is the brightest spot in the interference pattern, located directly in line with the two slits, where the light waves have traveled the same distance and interfere constructively.

  • How are the positions of the bright and dark fringes determined?

    -The positions of the bright and dark fringes are determined by the path length difference between the light waves from the two slits and the conditions for constructive and destructive interference.

  • What is the formula used to calculate the position of the first dark fringe in the script?

    -The formula used is \( y = \frac{\lambda L}{2D} \), where \( \lambda \) is the wavelength of the light, \( L \) is the distance from the slits to the screen, and \( D \) is the distance between the slits.

  • What is the formula used to calculate the position of the first bright fringe?

    -The formula used is \( y = \frac{\lambda L}{D} \), which is derived from the condition that the extra distance traveled by the light wave is equal to the full wavelength.

  • How does the script explain the relationship between the angles and the path length difference?

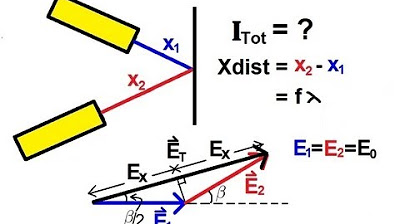
    -The script explains that for very small angles, the sine of the angle is approximately equal to the tangent of the angle, which allows the path length difference to be expressed in terms of the geometry of the setup.

  • What is the general pattern for finding the positions of the bright and dark spots in the interference pattern?

    -To find the bright spots (maxima), set the extra distance traveled equal to an integer number times the wavelength. To find the dark spots, set the extra distance traveled equal to an odd multiple of half the wavelength.

Outlines
00:00
🌟 Introduction to Light Interference and Young's Double Slit Experiment

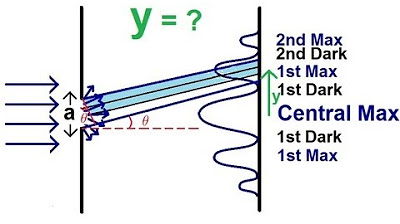
This paragraph introduces the concept of light interference, specifically focusing on the Young's double slit experiment. It explains how light passing through two closely spaced slits creates an interference pattern on a screen. The pattern consists of alternating bright and dark fringes due to constructive and destructive interference. The central maximum is highlighted as the point of maximum constructive interference. The paragraph sets the stage for understanding how to calculate the positions of these fringes based on the wavelength of light, the distance between the slits, and the distance to the screen.

05:02
πŸ“ Calculating the Positions of Interference Fringes

This paragraph delves into the mathematical aspect of determining the positions of the bright and dark fringes in the interference pattern. It uses the geometry of the Young's double slit setup to derive the relationship between the extra path length traveled by the light waves and the angles they make with the perpendicular. The conditions for constructive and destructive interference are explained, with the path length differences corresponding to integer multiples of the wavelength for bright fringes and half-integer multiples for dark fringes. An example with specific values for the wavelength, distance to the screen, and slit separation is provided to illustrate the calculation of the first dark and bright fringes.

10:02
πŸ” Further Exploration of Interference Fringes and Their Calculation

Building on the previous explanation, this paragraph continues to explore the calculation of interference fringes, focusing on finding the second dark and bright spots. The general formula for determining the positions of maxima (bright spots) and minima (dark spots) is established, emphasizing the relationship between the extra path length and the integer or half-integer multiples of the wavelength. The paragraph also highlights the regularity in the spacing of the fringes and how the pattern repeats for both directions from the central maximum, providing a comprehensive understanding of the interference pattern formation in Young's double slit experiment.

Mindmap
Keywords
πŸ’‘Young's Double Slit
Young's Double Slit is an experimental setup used to demonstrate the wave nature of light and other particles, showing interference patterns when light passes through two closely spaced slits. In the video, it is the central theme, illustrating how light diffracts and creates interference patterns on a screen, which are crucial to understanding the fundamental principles of quantum mechanics.
πŸ’‘Interference Pattern
An interference pattern is a series of alternating bright and dark bands that occur due to the superposition of waves. In the context of the video, these patterns are observed on a screen after light passes through two slits, demonstrating constructive and destructive interference, which is central to the experiment's purpose.
πŸ’‘Diffraction
Diffraction refers to the bending of waves around obstacles or the spreading out of waves after passing through an aperture. In the video, when light passes through the two slits, it diffracts, causing the light to spread out and create the interference pattern on the screen.
πŸ’‘Wavelength
The wavelength of light is the distance between two consecutive peaks (or troughs) of a wave, and it plays a significant role in the interference pattern observed. The video script mentions the wavelength as a key parameter in calculating the positions of the bright and dark fringes in the interference pattern.
πŸ’‘Constructive Interference
Constructive interference occurs when two or more waves meet in phase, resulting in a wave with an amplitude that is the sum of the individual amplitudes. In the video, constructive interference is responsible for the bright fringes in the pattern, where the light waves from both slits add together to produce a brighter spot.
πŸ’‘Destructive Interference
Destructive interference happens when two or more waves meet out of phase, leading to a reduction in amplitude or even cancellation. The video describes how destructive interference results in dark fringes where the light waves from the slits cancel each other out, leading to no light at those points.
πŸ’‘Path Length Difference
The path length difference is the difference in the distance traveled by waves from the two slits to a particular point on the screen. The script explains that constructive interference occurs when this difference is an integer multiple of the wavelength, while destructive interference occurs when it is an odd multiple of half a wavelength.
πŸ’‘Fringes
Fringes in the context of the video refer to the alternating bright and dark bands that make up the interference pattern. The script discusses how to calculate the positions of these fringes based on the path length difference and the geometry of the setup.
πŸ’‘Central Maximum
The central maximum is the brightest part of the interference pattern, located directly in line with the two slits. The script mentions it as the starting point for observing the fringes, where the light waves from both slits have traveled the same distance to the screen.
πŸ’‘Slits
In the video, the term 'slits' refers to the two narrow openings through which light passes to create the interference pattern. The distance between the slits, denoted as 'D' in the script, is a critical parameter in determining the spacing of the fringes.
πŸ’‘Bright Spots and Dark Spots
Bright spots and dark spots are specific locations on the interference pattern where constructive and destructive interference occur, respectively. The script explains how to calculate the positions of these spots on the screen based on the wavelength, the distance to the screen, and the distance between the slits.
Highlights

Introduction to the concept of light interference in Young's double slit experiment.

Explanation of how light defraction occurs through two closely spaced slits, leading to an interference pattern.

Description of the interference pattern consisting of alternating bright and dark fringes.

The importance of the path length difference in creating constructive or destructive interference.

Identification of the central maximum in the interference pattern.

Explanation of the first dark spots as a result of destructive interference.

Calculation of the path length difference to determine the positions of bright and dark fringes.

How to find the location of the first maximum using the geometry of the light paths.

The relationship between the extra distance traveled by light and the formation of maxima.

The use of trigonometric relationships to calculate the positions of interference fringes.

The formula for calculating the position of the first dark fringe in the interference pattern.

Application of the formula to find the distance to the first dark spot using specific values.

Calculation of the position of the first bright spot or maximum in the interference pattern.

The pattern of increasing distances between successive bright and dark fringes.

General method for finding the positions of bright spots by setting the extra distance to integer multiples of the wavelength.

General method for finding the positions of dark spots by setting the extra distance to half-integer multiples of the wavelength.

The symmetry of the interference pattern in both directions from the central maximum.

Summary of the principles behind the formation of interference fringes in Young's double slit experiment.

Transcripts

Browse More Related Video

Physics - Diffraction of Light (1 of 4) The Thin Slit

Waves part 2 (Double Slit, Single Slit, and Standing Waves)

Interference Patterns

Quantum mechanics and the double slit experiment

Physics 60 Interference of Light (1 of 8) Path and Phase Difference: Introduction

Physics 60 Interference of Light (3 of 8) Path and Phase Difference: General Case

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Light InterferenceYoung's ExperimentDouble SlitWave PhenomenaPhysics TutorialConstructive InterferenceDestructive InterferenceOpticsEducational ContentScience Learning