Physics 60 Interference of Light (1 of 8) Path and Phase Difference: Introduction

Michel van Biezen
13 May 201308:16
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the fascinating phenomenon of light interference, highlighting the effects of path and phase differences on light waves. It explains how constructive and destructive interference occur when two light beams with identical wavelengths and intensities travel different distances, leading to either an amplification or cancellation of light intensity. The script further clarifies the underlying principles of electromagnetic wave oscillations and how they contribute to the interference patterns observed, concluding with the intriguing outcome that in-phase beams can result in a fourfold increase in light intensity.

Takeaways
  • 🌟 The script discusses the phenomenon of light interference, a fundamental aspect of physics.
  • 🔍 It focuses on how the path and phase difference of light waves lead to interference patterns when two beams of light with the same wavelength and intensity meet.
  • 📏 Constructive interference occurs when the path length difference is an integer multiple of wavelengths, meaning the waves are in phase and reinforce each other.
  • 🚫 Destructive interference happens when the path length difference is an odd multiple of half wavelengths, causing the waves to be out of phase and cancel each other out.
  • 🌀 Light is described as an electromagnetic wave with electric and magnetic field oscillations, which are crucial for understanding interference.
  • 📶 The electric field oscillations of coherent light waves can either add up (constructive interference) or cancel out (destructive interference) based on their phase relationship.
  • 🔢 The intensity of light is proportional to the square of the electric field oscillations, which is a key factor in calculating the resulting intensity after interference.
  • 💡 When two in-phase light beams combine, the total intensity is four times the intensity of a single beam, demonstrating a significant amplification effect.
  • 📉 Conversely, if the beams are out of phase, the total intensity can drop to zero due to destructive interference.
  • 📚 The script provides a mathematical perspective on light interference, including the role of wavelength, path difference, and the vector nature of electric fields.
  • 📈 Understanding light interference is important for various applications in physics and optics, such as in the design of optical instruments and experiments.
Q & A

  • What is the interference of light?

    -The interference of light is a phenomenon where two or more light waves overlap and combine, resulting in increased or decreased brightness based on their phase relationship.

  • What conditions are necessary for two light beams to interfere constructively?

    -Constructive interference occurs when the path length difference between the two beams is an integer multiple of the wavelength, meaning they are in phase when they meet at the same point.

  • What is meant by the term 'destructive interference'?

    -Destructive interference happens when the path length difference is an odd multiple of half the wavelength, causing the light waves to be out of phase and cancel each other out, resulting in darkness.

  • How does the phase difference between two light beams affect the interference pattern?

    -The phase difference determines whether the interference is constructive or destructive. An integer number of wavelengths difference results in constructive interference, while an odd multiple of half a wavelength results in destructive interference.

  • What is the relationship between the path length difference and the interference of light?

    -The path length difference between two light beams determines the interference pattern. If the difference corresponds to an integer multiple of wavelengths, constructive interference occurs, while a half-integer multiple leads to destructive interference.

  • Why does light interfere when it is an electromagnetic wave?

    -Light interferes because it is an electromagnetic wave with oscillating electric and magnetic fields. When two coherent light beams meet, their electric field oscillations can either add up or cancel out, depending on their phase relationship.

  • How can the intensity of light be calculated when two beams interfere constructively?

    -When two beams interfere constructively, the total intensity is the sum of the squares of the electric field amplitudes of each beam. If the beams have the same intensity, the total intensity is four times the intensity of one beam.

  • What happens to the intensity of light when two beams interfere destructively?

    -During destructive interference, the electric field oscillations of the two beams are in opposite directions, leading to a cancellation effect. The total intensity in this case is zero, resulting in no light being observed.

  • How is the intensity of light related to the electric field oscillations?

    -The intensity of light is proportional to the square of the electric field oscillations. This means that the brightness of light is determined by the magnitude of the electric field amplitude.

  • Can you provide an example of how the path difference affects the interference pattern?

    -If the path difference is exactly one wavelength (λ), two wavelengths (2λ), or any integer multiple of the wavelength, the light waves will be in phase and constructive interference will occur. If the path difference is half a wavelength (λ/2), one and a half wavelengths (3λ/2), or any odd multiple of half a wavelength, destructive interference will occur.

  • What is the significance of the term 'coherent' in the context of light interference?

    -Coherent light sources emit waves with a constant phase relationship. This coherence is necessary for interference patterns to form, as it ensures that the light waves maintain a consistent relationship over time and space.

Outlines
00:00
🌟 Light Interference and Phase Difference

This paragraph delves into the fascinating phenomenon of light interference, focusing on the impact of path and phase differences. It explains how two beams of light with identical wavelength and intensity can interfere constructively or destructively depending on the path length difference. Constructive interference occurs when the extra distance traveled by one beam is an integer multiple of the wavelength, while destructive interference happens when this distance is an odd multiple of half a wavelength. The paragraph also touches on the physical reasons behind this behavior, relating it to the vector nature of electric and magnetic field oscillations in electromagnetic waves.

05:01
🔍 Calculating Intensity in Light Interference

The second paragraph explores how to calculate the intensity of light, particularly when two beams interfere. It begins by defining the intensity of a single beam and then discusses the scenario when two beams combine, either in or out of phase. The intensity of two in-phase beams is shown to be four times that of a single beam, highlighting a significant principle of light interference. The explanation involves the RMS value of electric field oscillations and the vector addition of these fields when beams are combined. This leads to the conclusion that the total intensity is maximized when the beams are perfectly in phase, as in the case of constructive interference.

Mindmap
Keywords
💡Interference of Light
Interference of light refers to the phenomenon where two or more light waves superimpose to form a resultant wave of greater, lower, or the same amplitude. In the video, this concept is central to understanding how light behaves when two beams with the same wavelength and intensity interact. The script discusses how constructive and destructive interference occur depending on the path length difference, which is a fundamental aspect of wave optics.
💡Path Difference
Path difference is the difference in the optical path lengths that light travels from two coherent sources to a common point. The script explains that when the path difference is an integer multiple of wavelengths, constructive interference occurs, while a half-integer multiple results in destructive interference. This is crucial for understanding the conditions under which light waves reinforce or cancel each other out.
💡Phase Difference
Phase difference is the difference in phase angles between two waves at a given point in time. In the context of the video, phase difference is directly related to the path difference and determines whether the interference is constructive or destructive. When the phase difference is zero or an even multiple of 2π, the waves are in phase and constructive interference occurs, as explained with the example of path lengths being equal or differing by an integer number of wavelengths.
💡Constructive Interference
Constructive interference happens when the crests of two waves align with each other, resulting in a wave with an amplitude that is the sum of the individual amplitudes. The video script illustrates this with the scenario where the path length difference is an integer multiple of the wavelength, leading to an increased intensity at the point of superposition.
💡Destructive Interference
Destructive interference occurs when the crest of one wave aligns with the trough of another, leading to a cancellation of the waves and a resultant wave with reduced or zero amplitude. The script describes this as happening when the path difference is a half-integer multiple of the wavelength, resulting in a dark spot where the light intensity is zero.
💡Coherent Sources
Coherent sources are light sources that emit waves with a constant phase relationship, allowing for interference effects to occur. The video emphasizes that for interference to be observed, the light sources must have the same wavelength, frequency, and intensity, which is a key condition for the interference of light.
💡Electric Field Oscillations
Electric field oscillations are the periodic changes in the electric field strength of an electromagnetic wave, such as light. The script explains how, during constructive interference, the electric field oscillations of the two waves add up vectorially to produce a stronger resultant field, while during destructive interference, they oppose each other, leading to cancellation.
💡Vector Addition
Vector addition is the process of combining two or more vectors to find the resultant vector. In the context of the video, it is used to describe how the electric field oscillations of two light waves combine during interference. The script mentions that when waves are in phase, their electric fields add up to double the amplitude, while being out of phase results in cancellation.
💡Intensity of Light
The intensity of light is a measure of the amount of light energy passing through a unit area per unit time. The video script relates this to the square of the electric field oscillations, explaining that the intensity of light is proportional to the square of the electric field amplitude. This concept is essential for understanding how the intensity changes during constructive and destructive interference.
💡RMS Value
RMS (Root Mean Square) value is a statistical measure of the magnitude of a varying quantity. In the script, it is mentioned in relation to the electric field oscillations, where the RMS value is used to describe the effective amplitude of the oscillations for calculating the intensity of light. This is important for understanding the average effect of the oscillations over time.
💡Epsilon Sub Naught (ε₀)
Epsilon sub naught, denoted as ε₀, is the electric constant or permittivity of free space, a fundamental physical constant that appears in the equations of electromagnetism. The script uses ε₀ in the formula for calculating the intensity of light, showing its importance in the relationship between electric field oscillations and light intensity.
Highlights

The lecture discusses the interference of light, focusing on the path and phase difference of light waves.

Two beams of light with the same wavelength and intensity can interfere constructively or destructively depending on their path length difference.

Constructive interference occurs when the path length difference is an integer multiple of wavelengths.

Destructive interference happens when the path length difference is an odd multiple of half-wavelengths.

Light is an electromagnetic wave with electric and magnetic field oscillations that can cancel each other out.

Coherent light sources with the same frequency and intensity can exhibit interference patterns.

Electric field oscillations can add vectorially, resulting in constructive or destructive interference.

The intensity of light is proportional to the square of the electric field oscillations' magnitude.

When two in-phase beams combine, their total intensity is four times the intensity of a single beam.

The intensity of light is calculated using the average or RMS value of the electric field oscillations.

The formula for light intensity involves the permittivity of free space and the speed of light.

The interference of light can be observed as bright or dark spots on a screen due to constructive or destructive interference.

When two beams are perfectly in phase, their combined intensity is maximized.

The phase difference between two light beams is crucial for determining the type of interference observed.

The path length difference between two beams affects the intensity of light when they interfere.

Understanding the interference of light is fundamental to various applications in physics and optics.

The lecture provides a clear explanation of how to determine the intensity of light in the presence of interference.

The principles of light interference have practical implications in fields such as fiber optics and holography.

Transcripts

Browse More Related Video

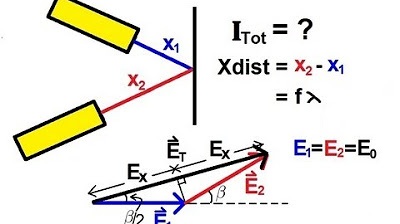
Physics 60 Interference of Light (3 of 8) Path and Phase Difference: General Case

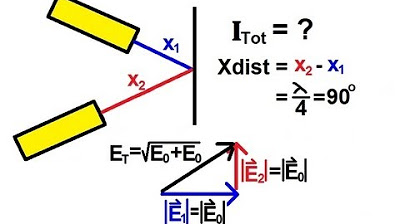
Physics 60 Interference of Light (2 of 8) Path and Phase Difference

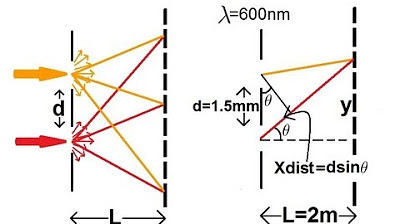
Physics 60 Interference of Light (4 of 8) Young's Double Slit

Interference Patterns

Waves part 2 (Double Slit, Single Slit, and Standing Waves)

18. Wave Theory of Light

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Light InterferencePhysics ConceptConstructiveDestructivePhase DifferenceWavelengthIntensityElectromagnetic WavesVector AdditionEducational Content