Physics - Diffraction of Light (1 of 4) The Thin Slit

Michel van Biezen
14 May 201314:04
EducationalLearning
32 Likes 10 Comments

TLDRThis lecture delves into the phenomenon of light diffraction, particularly through a single slit, creating a diffraction pattern distinct from interference. It explains how light passing through a narrow slit forms a central maximum and secondary fringes, both bright and dark. The lecture uses geometrical optics to derive the conditions for these fringes, illustrating how path length differences lead to constructive and destructive interference. It provides a step-by-step calculation for the positions of the first dark and bright spots, using the slit width, wavelength, and distance to the screen, revealing the non-linear relationship between them.

Takeaways
  • 🌟 Light interference typically involves multiple sources, but single-slit diffraction is a related phenomenon where light waves bend and interfere as they pass through a narrow opening.
  • 🔍 The central maximum in both double-slit and single-slit diffraction patterns is the brightest spot directly opposite the slit, but in single-slit diffraction, it is notably brighter than the side maxima.
  • 📏 The formation of dark spots in a diffraction pattern is due to destructive interference between different parts of the light wave that has passed through the slit.
  • 📐 The path length difference between rays from different parts of the beam through the slit leads to constructive or destructive interference, creating the pattern of bright and dark fringes.
  • 🧭 The condition for the first dark spot in a single-slit diffraction pattern is when the extra distance traveled by a ray is half a wavelength ( \( \frac{\lambda}{2} \) ) out of phase with another ray.
  • 📏 The formula to find the position of the first dark spot from the central maximum is \( y = \frac{\lambda L}{a} \), where \( a \) is the width of the slit, \( L \) is the distance to the screen, and \( \lambda \) is the wavelength of light.
  • 🔢 For the first bright spot or maximum, the condition involves a path difference that results in constructive interference, with the extra distance traveled by the top ray being \( \frac{\lambda}{2} \) out of phase with the ray one-third into the beam.
  • 📏 The formula to find the position of the first bright spot from the central maximum is \( y = \frac{3\lambda L}{2a} \), following the same variables as before but adjusted for the one-third path difference.
  • 🔢 The pattern for finding subsequent dark and bright spots involves setting the extra distance traveled by the top ray to be \( \frac{m\lambda}{2} \), where \( m \) is an odd integer for dark spots and an even integer for bright spots.
  • 📚 The relationship between the positions of the dark and bright spots is not linear; as the angle increases, the distance between successive spots decreases, following the diffraction pattern's mathematical progression.
Q & A

  • What is the main topic discussed in the video script?

    -The main topic discussed in the video script is the diffraction of light, particularly how it occurs with a single slit and the formation of diffraction patterns.

  • What is the central maximum in the context of diffraction patterns?

    -The central maximum is the bright spot that appears directly across from the slit in a diffraction pattern, similar to the central spot in a double-slit experiment but much brighter.

  • What causes the appearance of dark spots in a diffraction pattern?

    -Dark spots in a diffraction pattern appear due to destructive interference. This happens when various portions of the light beam traveling different paths interfere with each other out of phase, leading to cancellation of light at those points.

  • How is the path length difference related to the formation of dark spots in a diffraction pattern?

    -The path length difference is crucial for the formation of dark spots. When the path length difference equals half a wavelength (λ/2), destructive interference occurs, resulting in a dark spot on the screen.

  • What is the formula used to calculate the position of the first dark spot in a diffraction pattern?

    -The formula used to calculate the position of the first dark spot is y = (λ * L) / (a/2), where y is the distance from the central maximum, λ is the wavelength of light, L is the distance to the screen, and a is the width of the slit.

  • What is the significance of the slit width in diffraction patterns?

    -The slit width (a) plays a significant role in diffraction patterns. A smaller slit width results in more pronounced diffraction effects and a wider range of angles for constructive and destructive interference, affecting the pattern's spacing and intensity.

  • How does the distance to the screen (L) affect the diffraction pattern?

    -The distance to the screen (L) affects the size and spacing of the diffraction pattern. A larger distance to the screen results in a larger pattern, with the fringes (both bright and dark spots) spaced further apart.

  • What is the condition for the formation of the first bright spot or maximum in a diffraction pattern?

    -The first bright spot or maximum is formed when the extra distance traveled by the top ray of the beam equals one-third of the slit width times the sine of the angle (a/3 * sin(θ)) and equals half the wavelength (λ/2), leading to constructive interference.

  • How can you find the position of the second dark spot in a diffraction pattern?

    -The position of the second dark spot can be found by setting the extra distance traveled by the top ray of the beam equal to one-fourth of the slit width times the sine of the angle (a/4 * sin(θ)) and equal to half the wavelength (λ/2), resulting in destructive interference.

  • What is the general pattern for finding the positions of dark and bright spots in a diffraction pattern?

    -The general pattern involves setting the extra distance traveled by the top ray of the beam equal to (a/n) * sin(θ), where n is an odd number for bright spots and an even number for dark spots, and equating it to λ/2 for dark spots or λ for bright spots, then solving for the position y.

Outlines
00:00
🌟 Light Diffraction and Central Maximum

This paragraph introduces the concept of light diffraction through a single slit, which results in a diffraction pattern distinct from interference patterns. The central maximum is highlighted as the brightest spot directly opposite the slit. It explains how light waves passing through the slit interfere with each other, creating a pattern with a brighter central maximum and dimmer side maxima. The paragraph delves into the conditions that lead to the formation of dark spots, specifically when the path length difference equals half the wavelength, resulting in destructive interference. It also provides a mathematical formula to calculate the position of the first dark spot from the central maximum, given the slit width, wavelength, and distance to the screen.

05:01
🔍 Calculating Diffraction Pattern Positions

The second paragraph focuses on the mathematical derivation for determining the positions of dark and bright spots in a single-slit diffraction pattern. It uses the example of a 0.01 mm wide slit to calculate the distance to the first dark spot, which occurs at 1.2 cm from the central maximum, given a wavelength of 600 nm and a screen distance of 2 m. The explanation involves setting up the condition for destructive interference and solving for the position 'y' using the relationship between the slit width, wavelength, and the tangent of the angle of diffraction. The paragraph also discusses the calculation for the first bright spot, which is less intense than the central maximum, and explains the pattern for finding subsequent dark and bright spots by adjusting the fraction of the beam considered.

10:06
📐 Advanced Diffraction Pattern Analysis

The final paragraph builds upon the previous discussion by explaining how to find the positions of the second dark and bright spots in the diffraction pattern. It describes the process of dividing the beam into four and five equal parts to find these spots, respectively. The conditions for destructive and constructive interference are detailed, with the extra distance traveled by the light rays set equal to half the wavelength (for dark spots) and a fraction of the wavelength (for bright spots). The paragraph provides a step-by-step guide to finding the positions of these fringes, emphasizing the non-linear relationship between them and the central maximum. It concludes with a general formula for finding the positions of subsequent dark and bright spots in the diffraction pattern, illustrating the pattern of increasing the denominator in the sine term for each subsequent spot.

Mindmap
Keywords
💡Diffraction
Diffraction is the bending of waves around the edges of an obstacle or aperture into the region of geometrical shadow of the obstacle. In the context of the video, it refers to the pattern formed when light waves pass through a single narrow slit, creating a series of bright and dark fringes on a screen. The script describes how light diffracts to form a central maximum and subsequent maxima and minima, demonstrating the wave nature of light.
💡Interference
Interference is a phenomenon in which two waves superpose to form a resultant wave of greater, lower, or the same amplitude. The video discusses how interference occurs in a single-slit setup, albeit different from a double-slit experiment, and results in the constructive and destructive superposition of light waves, leading to the formation of a diffraction pattern.
💡Central Maximum
The central maximum is the brightest spot in a diffraction pattern that appears directly opposite the slit or aperture. The script explains that, similar to a double-slit system, the central maximum is significantly brighter than the other maxima in a single-slit diffraction pattern.
💡Path Length Difference
Path length difference refers to the difference in the optical path lengths that different parts of a wavefront travel before reaching a point. In the video, the concept is used to explain how destructive interference leads to dark spots in the diffraction pattern when the path length difference equals half a wavelength.
💡Wavelength
The wavelength is the distance between two corresponding points in consecutive cycles of a wave. The script uses the term to describe the condition for destructive interference, where the path length difference equals half the wavelength, leading to the formation of dark spots in the diffraction pattern.
💡Bright Spots
Bright spots, also known as maxima, are areas of constructive interference in a diffraction pattern where the waves from the slit reinforce each other. The video explains that these spots are less intense than the central maximum but are still visible as secondary bright areas alongside the central maximum.
💡Dark Spots
Dark spots, or minima, are areas in a diffraction pattern where destructive interference occurs, resulting in no light reaching that point. The script describes how dark spots are formed when the path length difference between different parts of the light wave equals half the wavelength, leading to cancellation of the light waves.
💡Beam Width
Beam width refers to the physical size of the light beam as it passes through the slit. The video uses this term to explain how the finite width of the beam contributes to the interference pattern by causing different portions of the beam to interfere with each other.
💡Angle Theta
Angle Theta is the angle made by the light rays with respect to the normal (perpendicular) to the slit. The script uses this angle to describe the geometry of the light rays as they diffract and form the pattern on the screen, with the tangent of Theta being proportional to the path difference between rays at different heights of the beam.
💡Fringes
Fringes refer to the alternating bright and dark bands in a diffraction pattern. The video explains how these fringes are caused by the constructive and destructive interference of light waves after passing through a single slit, with the pattern repeating at regular intervals based on the slit width and wavelength.
💡Slit Width
Slit width is the physical dimension of the opening through which light passes. In the script, it is used to calculate the positions of the bright and dark spots in the diffraction pattern, with the formula Y = (m * λ * L) / a, where m is the order of the fringe, λ is the wavelength, L is the distance to the screen, and a is the slit width.
Highlights

Introduction to the concept of light interference and the difference between interference and diffraction.

Explanation of the central maximum in both double slit and single slit systems.

Formation of a diffraction pattern and its contrast with a double slit interference pattern.

The role of the finite width of the light beam in creating a diffraction pattern.

How the path length difference between different portions of the light beam leads to interference.

The condition for the appearance of a dark spot in a diffraction pattern: a/2 sin Theta = Lambda/2.

Calculation of the distance to the first dark spot from the central maximum using the given parameters.

The significance of the slit width (a) in determining the diffraction pattern.

How to find the position of the first bright spot or maximum in a diffraction pattern.

The relationship between the extra distance traveled by the light rays and the formation of bright spots.

The method to calculate the position of the second dark spot in the diffraction pattern.

The process of finding the second maximum or bright spot in the diffraction pattern.

The non-linear relationship between the positions of dark and bright spots in a diffraction pattern.

General formula for finding the positions of dark and bright spots in a diffraction pattern: a/n sin Theta = Lambda/2.

The pattern recognition in calculating fringe positions for diffraction through a single slit.

Practical application of the diffraction pattern in understanding the behavior of light through small apertures.

Transcripts

Browse More Related Video

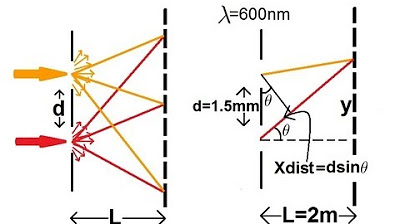
Physics 60 Interference of Light (4 of 8) Young's Double Slit

Waves part 2 (Double Slit, Single Slit, and Standing Waves)

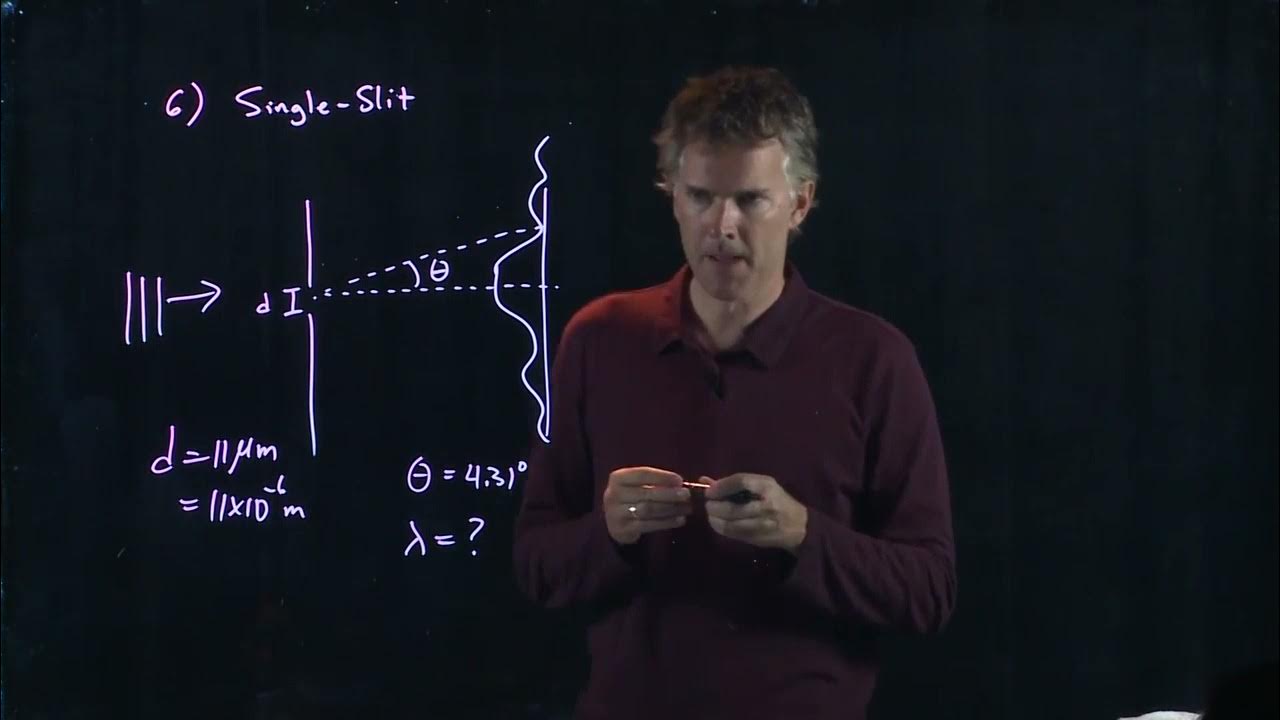
Single Slit Interference | Physics with Professor Matt Anderson | M28-19

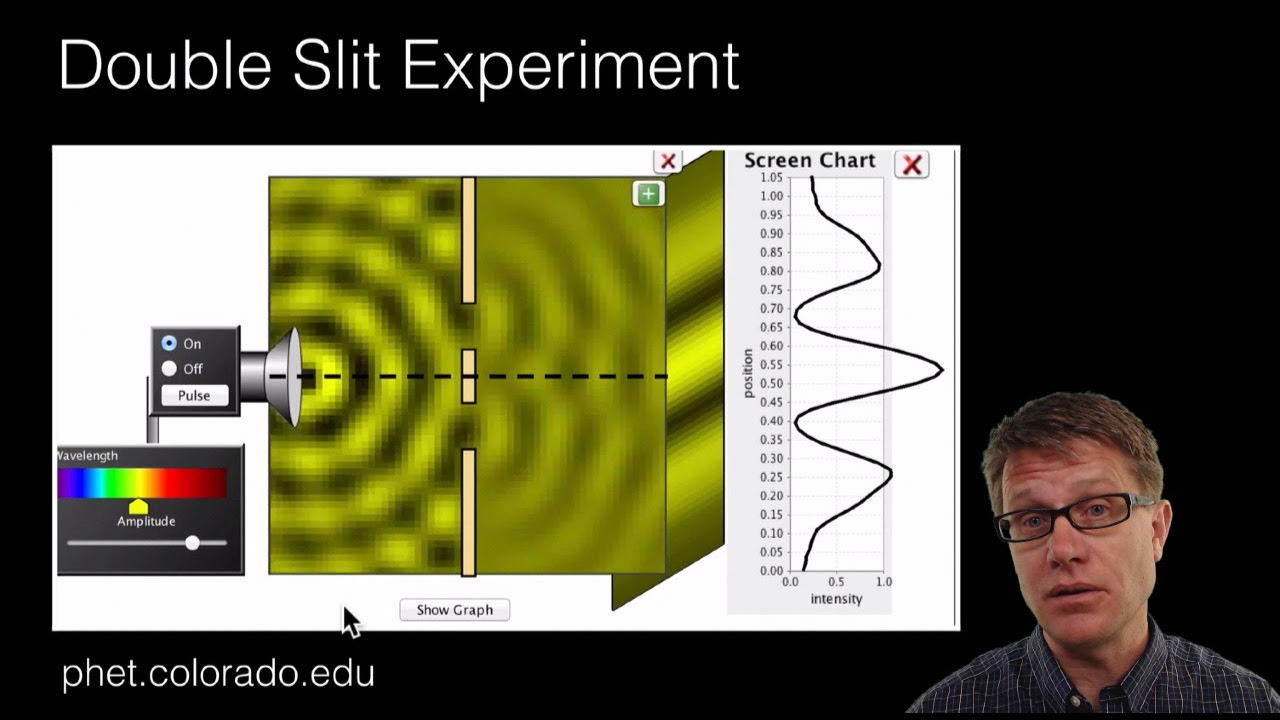
Interference Patterns

Light Is Waves: Crash Course Physics #39

Single Slit Diffraction | Physics with Professor Matt Anderson | M28-16

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Light DiffractionInterference PatternsSingle SlitDouble SlitPhysics LessonWave TheoryConstructive InterferenceDestructive InterferenceDiffraction PatternEducational Video