Finding the Tension and Acceleration for a Two Mass Pulley (with Friction)

PhysAssistant
18 Dec 202311:59
EducationalLearning
32 Likes 10 Comments

TLDRThis video script explores a physics problem involving two masses connected by a frictionless pulley. Mass M1, weighing 10 kg, is on a surface with a kinetic friction coefficient of 0.18, while Mass M2, at 12 kg, hangs over the edge. The script guides viewers through calculating the acceleration of the masses and the tension in the rope, emphasizing the importance of considering the same tension and acceleration for both masses and the unique coordinate system setup. By solving a system of equations, the video reveals an acceleration of 4.5 m/s² and a tension of 64 Newtons, providing a clear explanation of pulley dynamics and the impact of friction.

Takeaways
  • 🔄 The problem involves two masses connected by a frictionless pulley system with one mass on a surface and the other hanging over the edge.
  • 📐 M1 has a mass of 10 kg and is on a surface with a coefficient of kinetic friction of 0.18, while M2 has a mass of 12 kg.
  • 🧲 The tension in the rope and the acceleration of the masses are the same for both M1 and M2 due to the connection by the string.
  • 📊 The coordinate system is adjusted to align with the direction of the rope, considering the forces acting on each mass in the x-axis direction.
  • 🚫 Friction on M1's surface is a factor and is calculated using the coefficient of kinetic friction multiplied by the normal force, which is the weight of M1.
  • 📉 The weight of M1 does not contribute to its motion in the y-direction but is crucial for calculating the frictional force.
  • 📈 For M2, the only forces acting are its weight (considered positive in the x-direction) and the tension from the rope (considered negative in the x-direction).
  • 🔍 Two equations are set up for the forces acting on M1 and M2, with two unknowns—tension (T) and acceleration (a).
  • ⚖️ The tension in the rope can be found by rearranging the equation for M2, which is M2g - M2a.
  • 📝 By substituting the tension into the equation for M1, a single equation with one unknown (acceleration) is obtained, which can be solved for 'a'.
  • 📊 The acceleration is calculated to be 4.5 m/s² by substituting the given values into the derived equation.
  • 🔑 With the acceleration known, the tension in the rope can be determined using the equation for M2, resulting in a tension of 64 Newtons.
Q & A

  • What is the problem described in the script about?

    -The problem involves two masses connected by a frictionless pulley system. One mass is on a surface with kinetic friction, and the other mass is hanging over the edge. The task is to find the acceleration of the masses and the tension in the rope.

  • What are the masses of the two objects in the problem?

    -The mass of the first object (M1) is 10 kg, and the mass of the second object (M2) is 12 kg.

  • What is the coefficient of kinetic friction for the surface M1 is on?

    -The coefficient of kinetic friction for the surface M1 is on is 0.18.

  • Why is the tension in the rope the same for both masses?

    -The tension in the rope is the same for both masses because they are connected by the same string, and thus they experience the same magnitude of tension, but in opposite directions.

  • How does the coordinate system work in this problem?

    -In this problem, the coordinate system is imagined to follow the path of the rope, turning at the pulley and continuing through both masses, with positive and negative directions assigned based on the forces acting along the rope.

  • What are the forces acting on M1?

    -The forces acting on M1 are the tension to the right, the friction force to the left, the weight (mg) acting vertically, and the normal force which is equal and opposite to the weight.

  • What are the forces acting on M2?

    -The forces acting on M2 are its weight (mg) acting in the positive x-direction and the tension of the cord, which is the same magnitude but in the opposite direction.

  • How many equations and unknowns are there to solve for in this problem?

    -There are two equations and two unknowns in this problem: one equation for the forces on M1 and one for M2, with the unknowns being the tension (T) and the acceleration (a).

  • What is the formula used to calculate the acceleration (a) in this problem?

    -The formula used to calculate the acceleration is \( a = \frac{m_2g - \mu_k m_1g}{m_1 + m_2} \), where \( m_2 \), \( g \), \( \mu_k \), and \( m_1 \) are the mass of M2, acceleration due to gravity, coefficient of kinetic friction, and mass of M1, respectively.

  • What is the calculated acceleration in meters per second squared?

    -The calculated acceleration is 4.5 m/s².

  • How is the tension in the rope calculated once the acceleration is known?

    -The tension in the rope is calculated using the equation \( T = m_2g - m_2a \), where \( m_2 \) is the mass of M2, \( g \) is the acceleration due to gravity, and \( a \) is the acceleration found from the previous calculation.

  • What is the calculated tension in Newtons?

    -The calculated tension in the rope is 64 Newtons.

Outlines
00:00
🔍 Analyzing Pulley System with Friction and Two Masses

This paragraph introduces a physics problem involving a pulley system with two masses, M1 and M2, connected by a frictionless pulley. M1 is on a surface with a kinetic friction coefficient of 0.18 and has a mass of 10 kg, while M2 hangs over the edge with a mass of 12 kg. The paragraph discusses the setup and the assumption that both masses will have the same acceleration and tension in the system. It also explains the unique coordinate system used in this problem, which involves considering the direction of forces acting on each mass and the importance of the normal force and weight in calculating friction.

05:01
📚 Setting Up Force Equations for the Pulley System

The second paragraph delves into setting up the force equations for both masses in the system. For M1, the equation accounts for the tension force to the right, the friction force to the left, and the normal force due to its weight. The friction force is calculated as the product of the kinetic friction coefficient and the normal force, which is the weight of M1. For M2, the forces considered are its weight acting downwards (considered positive in the x-direction for this scenario) and the tension force in the opposite direction. The paragraph then proceeds to solve for the tension by expressing it in terms of M2's weight and acceleration, and subsequently substituting this expression into the equation for M1 to find the acceleration.

10:03
🎯 Calculating Acceleration and Tension in the System

The final paragraph focuses on calculating the acceleration and tension in the pulley system. By solving the combined force equation, the acceleration is found to be 4.5 m/s². With the acceleration known, the tension in the rope is then calculated using the weight of M2 and the acceleration. The paragraph concludes by emphasizing the importance of understanding the system of equations with two unknowns and the conceptual approach to solving pulley problems, especially when one mass is on a surface with friction. It also invites viewers to ask for more topics and thanks them for watching.

Mindmap
Keywords
💡Forces
Forces are interactions between objects that cause a change in motion or shape. In the video, forces are central to understanding the dynamics of the pulley system with two masses. The script mentions tension and friction as forces affecting the masses, with tension being the pulling force in the rope and friction opposing the motion of mass one on the surface.
💡Pulley
A pulley is a simple machine that changes the direction of an applied force. In the context of the video, a frictionless pulley connects two masses, allowing them to exert forces on each other. The pulley is crucial in the problem as it ensures that the tension in the rope is the same for both masses, affecting their acceleration.
💡Masses
Masses in the video refer to the two objects with specific weights (10 kg and 12 kg) that are connected by a pulley. They are the primary subjects of the force analysis. The script discusses how the forces acting on these masses result in a common acceleration, which is a key concept in solving the problem.
💡Friction
Friction is a force that resists the relative motion of two surfaces in contact. The script specifies a coefficient of kinetic friction of 0.18 for mass one on the surface, which is essential in calculating the force of friction acting against the tension in the rope and thus the acceleration of the masses.
💡Coefficient of Kinetic Friction
The coefficient of kinetic friction (0.18 in the script) is a dimensionless scalar value that represents the ratio of the force of friction between two bodies in motion to the force pressing them together. It is used to calculate the frictional force acting on mass one, which opposes its motion.
💡Acceleration
Acceleration is the rate of change of velocity of an object. In the video, the script aims to find the common acceleration of both masses as they are connected by the pulley system. The acceleration is determined by the net force acting on the system, which is the result of the tension in the rope and the frictional force.
💡Tension
Tension is the force transmitted through a string, rope, or cable when it is pulled tight by opposing forces. In the script, tension is the force in the rope that pulls mass one to the right and mass two downward. The magnitude of tension is the same for both masses but in opposite directions, and it is a key unknown in the problem.
💡Coordinate System
A coordinate system is a standardized way of assigning a pair of numbers to every point in a plane. The script discusses the unconventional orientation of the coordinate system in this problem, with the rope effectively acting as the x-axis, which is essential for setting up the force equations correctly.
💡Force Equations
Force equations are mathematical expressions that relate the forces acting on an object to its motion, typically in the form of Newton's second law (F = ma). In the script, force equations are set up for both masses to solve for the unknowns: the acceleration and the tension in the rope.
💡Weight
Weight is the force exerted on an object due to gravity and is calculated as the product of mass and the acceleration due to gravity (mg). In the video, the weight of both masses is considered as a downward force, which is crucial in determining the net force and acceleration of the system.
💡Normal Force
The normal force is the perpendicular force exerted by a surface that supports the weight of an object resting on it. In the script, the normal force on mass one is equal in magnitude and opposite in direction to the weight of mass one, and it is used in calculating the frictional force.
Highlights

Problem involves two masses connected by a frictionless pulley with one on a surface and the other hanging over the edge.

M1 has a mass of 10 kg and is on a surface with a coefficient of kinetic friction of 0.18.

M2 has a mass of 12 kg and is hanging.

Tension and acceleration for both masses are the same due to the connection by the string.

Coordinate system is unconventional, with the rope acting as the axis for both masses.

Forces acting on M1 include tension to the right, friction to the left, and weight mg.

Friction force on M1 is calculated as the coefficient of kinetic friction times the normal force.

Forces on M2 are its weight mg in the positive direction and tension in the opposite direction.

Setting up force equations for both M1 and M2 to solve for unknowns tension and acceleration.

Tension for M1 is represented as T, and for M2 as m2g - m2a.

Acceleration a can be found by solving the combined equation of forces for M1 and M2.

Acceleration a is calculated as (m2g - μk * m1g) / (m1 + m2).

Plugging in the given values results in an acceleration of 4.5 m/s^2.

Tension is then calculated using the found acceleration and is 64 Newtons.

The problem-solving approach involves a system of two equations with two unknowns.

Understanding the pulley system dynamics is crucial, especially when one mass is on a frictional surface.

The method demonstrates how to manage complex pulley problems with varying forces.

The importance of considering the rope as an axis in these types of problems is emphasized.

Transcripts

Browse More Related Video

Treating systems (the hard way) | Forces and Newton's laws of motion | Physics | Khan Academy

2 Masses on a Pulley - Torque Demonstration

Incline Plane Problems with Friction

2019 AP Physics 1 Solutions Free Response #2

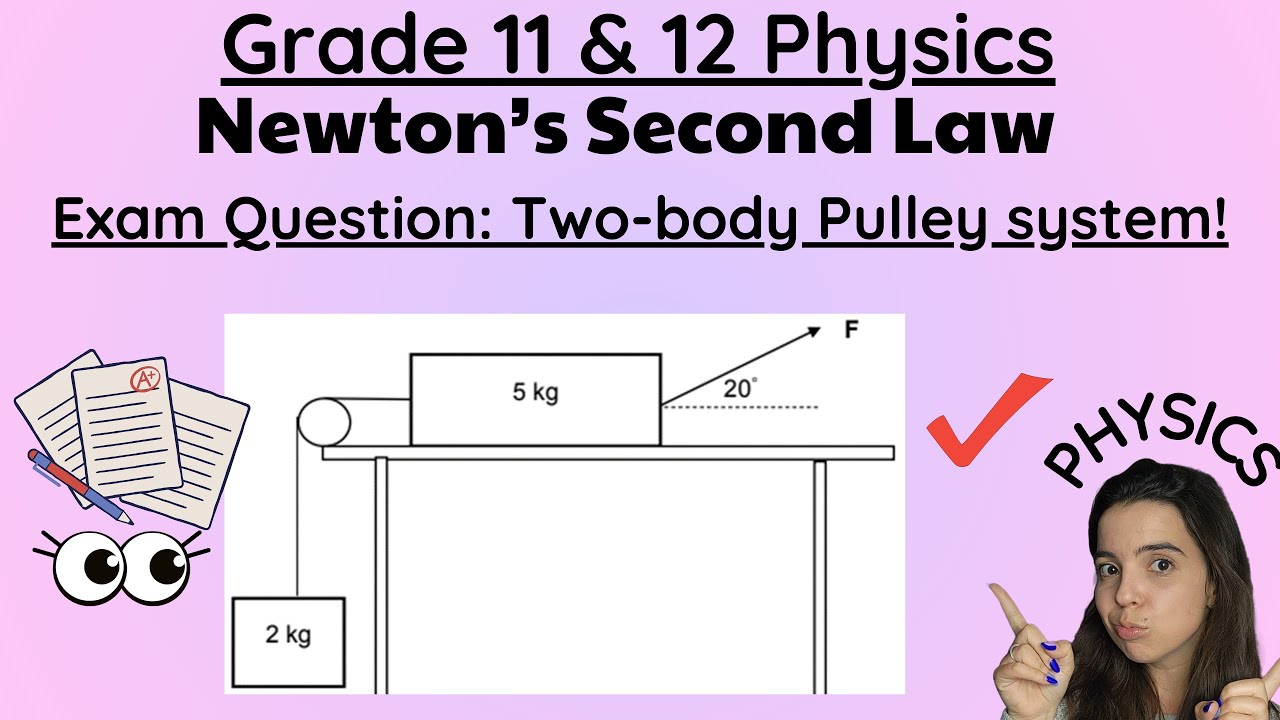
Newton's Second Law Exam Question: Two-body systems Pulley practice

2015 AP Physics 1 free response 1b

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsForcesPulleysFrictionAccelerationTensionKinetic CoefficientMass EquationsMomentumEducationalProblem Solving