Treating systems (the hard way) | Forces and Newton's laws of motion | Physics | Khan Academy

Khan Academy
29 Jul 201615:26
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a classic physics problem involving two masses, 3 kg and 5 kg, connected by a rope that passes over a pulley. The challenge is to determine the acceleration of each mass. The narrator explains the function of a pulley, which is to transfer force from one direction to another without loss, assuming no resistance or mass. The problem-solving approach begins with Newton's second law, applying it to both masses in their respective directions. Initially, this leads to two equations with two unknowns (acceleration and tension). The crucial insight is that the magnitudes of the accelerations must be equal due to the system's constraints, allowing the creation of a single equation with one unknown. After solving for the acceleration of the 5 kg mass, the acceleration of the 3 kg mass is easily found by using their relationship. The video concludes with a solution: the 5 kg mass accelerates at 3.68 m/s² horizontally, while the 3 kg mass accelerates at -3.68 m/s² vertically, indicating a downward motion. The methodical approach and the final solution are engaging, demonstrating the application of physics principles to real-world problems.

Takeaways
  • 📚 The problem presented involves two masses tied together by a rope passing over a pulley, and it's a classic physics problem found in textbooks.
  • 🔍 A pulley is a rotating mechanism that can transfer force from one direction to another, turning vertical forces into horizontal forces or vice versa.
  • 🎯 Newton's second law is used to find acceleration, which is the net force in a given direction divided by the mass.
  • 🔄 The forces acting on the 5 kg mass are gravity, a normal force, and a tension force to the right, while the 3 kg mass experiences gravity and tension.
  • 🧲 The tension in the rope is the same on both sides of the pulley if the pulley has negligible mass and no resistance.
  • 📐 A force diagram is essential to visualize and calculate the forces acting on each mass.
  • 🔁 The accelerations of the two masses are not independent; the 3 kg mass accelerates downward while the 5 kg mass accelerates horizontally, with equal magnitudes but opposite directions.
  • ⚖️ The key to solving the problem is recognizing that the magnitude of accelerations must be the same for both masses to maintain the integrity of the rope without breaking or stretching.
  • 🔢 The final step involves algebraic manipulation to solve for the acceleration of the 5 kg mass, which then allows for the calculation of the 3 kg mass's acceleration.
  • 📉 The acceleration of the 3 kg mass is found to be negative, indicating downward acceleration, while the 5 kg mass has a positive acceleration, indicating horizontal movement to the right.
  • 📈 The calculated acceleration for the 5 kg mass is approximately 3.68 meters per second squared, and for the 3 kg mass, it is -3.68 meters per second squared.
Q & A

  • What is the classic physics problem presented in the transcript?

    -The classic physics problem involves finding the acceleration of two masses tied together by a rope that passes over a pulley.

  • What is a pulley and how does it function in this problem?

    -A pulley is a small piece of plastic or metal that can rotate and has a groove for a string or rope to pass over. It allows the transfer of force from one direction to another, turning vertical forces into horizontal forces or vice versa.

  • Why is it assumed that the tension on both sides of the pulley is equal?

    -The tension is assumed to be equal because if the pulley can spin freely without resistance and has negligible mass, there is no reason for the tension to differ on either side.

  • What is Newton's second law as applied to this problem?

    -Newton's second law is used to find acceleration by stating that the acceleration in a given direction is equal to the net force in that direction divided by the mass.

  • How does the force diagram help in solving the problem?

    -The force diagram helps to visualize and account for all the forces acting on the masses, including gravity, normal force, and tension, which are necessary to apply Newton's second law.

  • What is the key argument made to link the accelerations of the two masses?

    -The key argument is that if the 3 kg mass moves down a certain amount, the 5 kg mass must move forward by the same amount to provide the necessary rope length. This implies that the magnitudes of their accelerations must be the same, with opposite signs due to the direction of movement.

  • Why is it necessary to consider both the vertical and horizontal directions when applying Newton's second law?

    -Considering both directions is necessary because the problem involves forces and accelerations in both the vertical (for the 3 kg mass) and horizontal (for the 5 kg mass) directions. This helps to account for all forces acting on the system.

  • How is the acceleration of the 5 kg mass in the horizontal direction related to the acceleration of the 3 kg mass in the vertical direction?

    -The acceleration of the 3 kg mass in the vertical direction is equal in magnitude but opposite in direction to the acceleration of the 5 kg mass in the horizontal direction. This is due to the system's constraint that the rope does not stretch or break.

  • What is the final calculated acceleration for the 5 kg mass in the horizontal direction?

    -The final calculated acceleration for the 5 kg mass in the horizontal direction is 3.68 meters per second squared.

  • What is the acceleration of the 3 kg mass, and why is it negative?

    -The acceleration of the 3 kg mass is -3.68 meters per second squared. It is negative because the mass is accelerating downward, and downward acceleration is considered negative in the given coordinate system.

  • What is the 'easy way' to solve such problems, which will be presented in the next video?

    -The 'easy way' to solve these problems is not detailed in the transcript, but it is implied that there is a more straightforward or simplified method that will be explained in the subsequent video, which would likely make use of the system's symmetry and constraints.

Outlines
00:00
📚 Introduction to the Physics Problem

The first paragraph introduces a classic physics problem involving two masses connected by a rope over a pulley. The pulley is explained as a device that can rotate freely to transfer force from one direction to another. The challenge is to find the acceleration of a 3 kg mass and a 5 kg mass. The speaker warns that they will first demonstrate the more complex method to solve the problem, as understanding this will make the simpler method clearer and is often required by educators.

05:02
🔍 Applying Newton's Second Law to Find Acceleration

The second paragraph delves into applying Newton's second law to find the acceleration of the 5 kg mass in the horizontal direction. The forces acting on the 5 kg mass are identified: gravity, normal force, and tension. A force diagram is used to visualize these forces. The speaker acknowledges the difficulty in solving the problem due to the unknown acceleration and tension. The approach then shifts to considering the 3 kg mass and its forces in the vertical direction, noting that the tension in the rope is the same on both sides of the pulley, assuming no resistance or mass from the pulley.

10:04
🔗 Linking the Accelerations of the Two Masses

The third paragraph discusses the crucial step of linking the accelerations of the two masses. The argument is made that for the system to work without the rope breaking or stretching, the 3 kg mass moving down must result in the 5 kg mass moving forward by the same amount. This leads to the conclusion that the magnitudes of acceleration for both masses must be the same, with opposite directions due to their respective movement. This insight allows the problem to be solved by combining the equations for both masses and solving for a single variable.

15:07
🧮 Solving for the Accelerations

The final paragraph walks through the algebraic process of solving for the acceleration of the 5 kg mass in the horizontal direction (A5X), using the relationship established between the accelerations of the two masses. After finding A5X to be 3.68 meters per second squared, the acceleration of the 3 kg mass (A3Y) is determined by using the previously established relationship, resulting in an acceleration of -3.68 meters per second squared, indicating downward movement. The paragraph concludes by summarizing the process: applying Newton's second law to both masses, linking their accelerations due to the system's constraints, and solving the resulting equation to find the accelerations.

Mindmap
Keywords
💡Pulley
A pulley is a wheel with a groove running around its circumference, designed to guide and change the direction of a rope or belt. In the context of the video, the pulley is essential for transferring force from one direction to another, allowing the system of masses and ropes to function. The pulley's ability to rotate freely without mass or friction is crucial for the tension in the rope to be equal on both sides.
💡Acceleration
Acceleration is the rate of change of velocity over time. It is a vector quantity that has both magnitude and direction. In the video, the problem at hand is to find the acceleration of two masses (3 kg and 5 kg) connected by a rope over a pulley. The concept is central to applying Newton's second law to determine the dynamics of the system.
💡Newton's Second Law
Newton's second law of motion states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = ma). In the video, this law is used to set up equations for the forces acting on the 3 kg and 5 kg masses, which are then solved to find their accelerations.
💡Tension
Tension refers to the force transmitted through a string, rope, cable, or similar object when it is pulled tight by forces acting from opposite ends. In the context of the video, tension is the force in the rope connecting the two masses and is used to calculate the accelerations of the masses. The assumption is made that the tension is the same on both sides of the pulley if the pulley is massless and frictionless.
💡Mass
Mass is a measure of the amount of matter in an object. In the video, there are two distinct masses, 3 kg and 5 kg, which are tied together by a rope and influenced by gravity and tension forces. The masses are central to the problem as their weights and the resulting dynamics are what the video aims to analyze and calculate.
💡Gravity
Gravity is the force by which a planet or other celestial body attracts objects toward its center. In the script, gravity acts on the masses, pulling them downward. The force of gravity on an object is calculated as the object's mass times the acceleration due to gravity (F_gravity = m * g, where g is approximately 9.8 m/s² on Earth).
💡Force Diagram
A force diagram is a graphical representation used to visualize all the forces acting on an object. In the video, the force diagram is used to illustrate the forces on the 5 kg and 3 kg masses, including gravity, normal force, and tension. This visual tool helps in applying Newton's second law to find the unknown accelerations and forces in the system.
💡Normal Force
The normal force is the support force exerted by a surface that opposes the force trying to compress the surface. In the video, the normal force acts upward on the 5 kg mass, balancing the force of gravity if the mass is not accelerating vertically. It is considered in the analysis to ensure that the vertical forces are balanced, allowing the focus to be on horizontal accelerations.
💡Friction
Friction is the force that resists the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. The video assumes there is no friction on the table or the pulley, which simplifies the problem by eliminating additional forces that would need to be accounted for in the calculations.
💡Rope Stretch
Rope stretch refers to the elongation of a rope under tension. In the video, it is assumed that any potential stretch in the rope is negligible, which allows the problem to be treated as if the rope does not change length. This assumption is critical for the argument that the 3 kg mass moving down by a certain amount necessitates the 5 kg mass moving forward by the same amount.
💡Direction
Direction refers to the course along which a force is applied or an object is moving. In the script, direction is crucial for understanding the dynamics of the system. The video specifies horizontal (X direction) for the 5 kg mass's acceleration and vertical (Y direction) for the 3 kg mass's acceleration. The direction of acceleration determines the sign of the acceleration in the equations.
Highlights

This is a classic physics problem involving two masses tied together by a rope passing over a pulley

The pulley is a rotating piece of plastic or metal that allows force to be transferred from one direction to another

If the pulley is massless and frictionless, the tension on both sides will be equal

Apply Newton's second law to find the acceleration of each mass by dividing the net force by the mass

Choose the horizontal direction for the 5 kg mass and the vertical direction for the 3 kg mass

Identify all the forces acting on each mass - gravity, normal force, and tension

Set up two equations for the net force on each mass, but you have two unknowns - acceleration and tension

Realize the accelerations of the two masses are not independent - they must have the same magnitude

The 3 kg mass has a downward acceleration while the 5 kg mass has an equal upward acceleration

Express the acceleration of the 3 kg mass in terms of the acceleration of the 5 kg mass

Substitute this relationship into one of the net force equations to eliminate the tension variable

Solve the resulting equation for the acceleration of the 5 kg mass in the horizontal direction

Find the acceleration to be 3.68 m/s^2 for the 5 kg mass and -3.68 m/s^2 for the 3 kg mass

The key insight is that the two masses must accelerate at the same rate to prevent the rope from breaking or stretching

This problem demonstrates the power of Newton's laws and the importance of free-body diagrams

The hard way of solving the problem involves setting up equations for both masses and linking their accelerations

In the next video, an easier method for solving this type of problem will be presented

Transcripts

Browse More Related Video

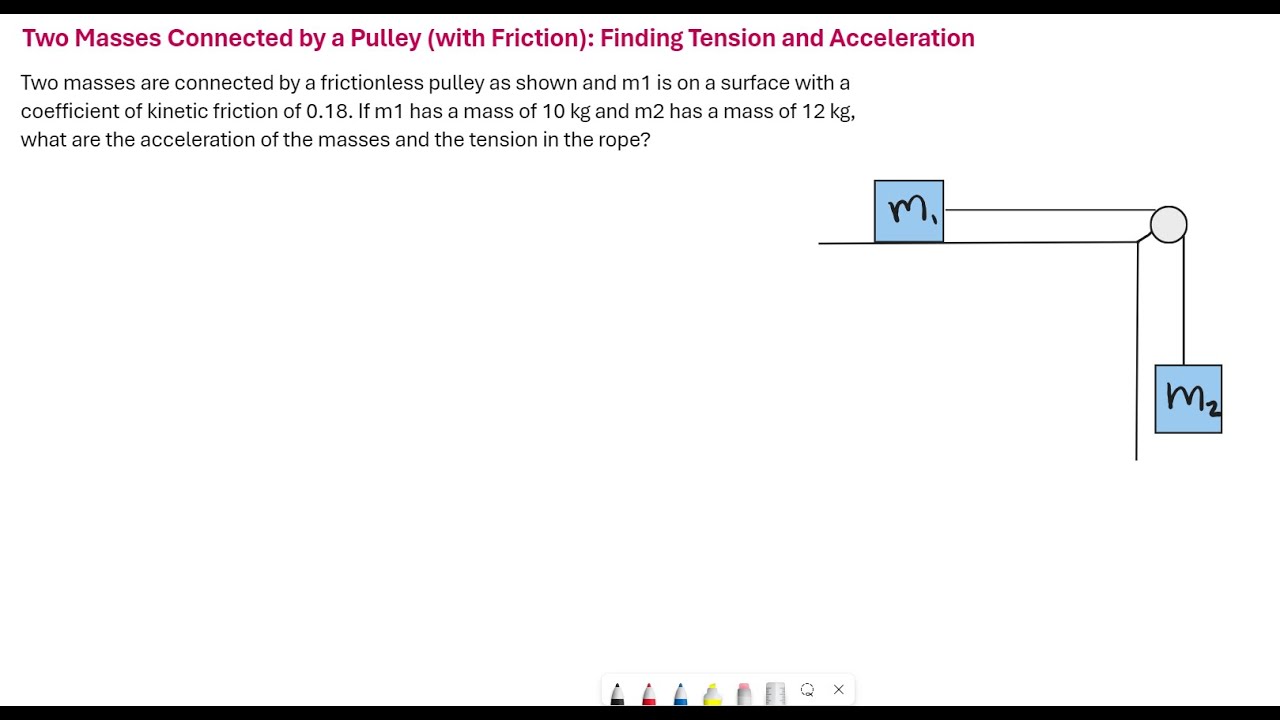
Finding the Tension and Acceleration for a Two Mass Pulley (with Friction)

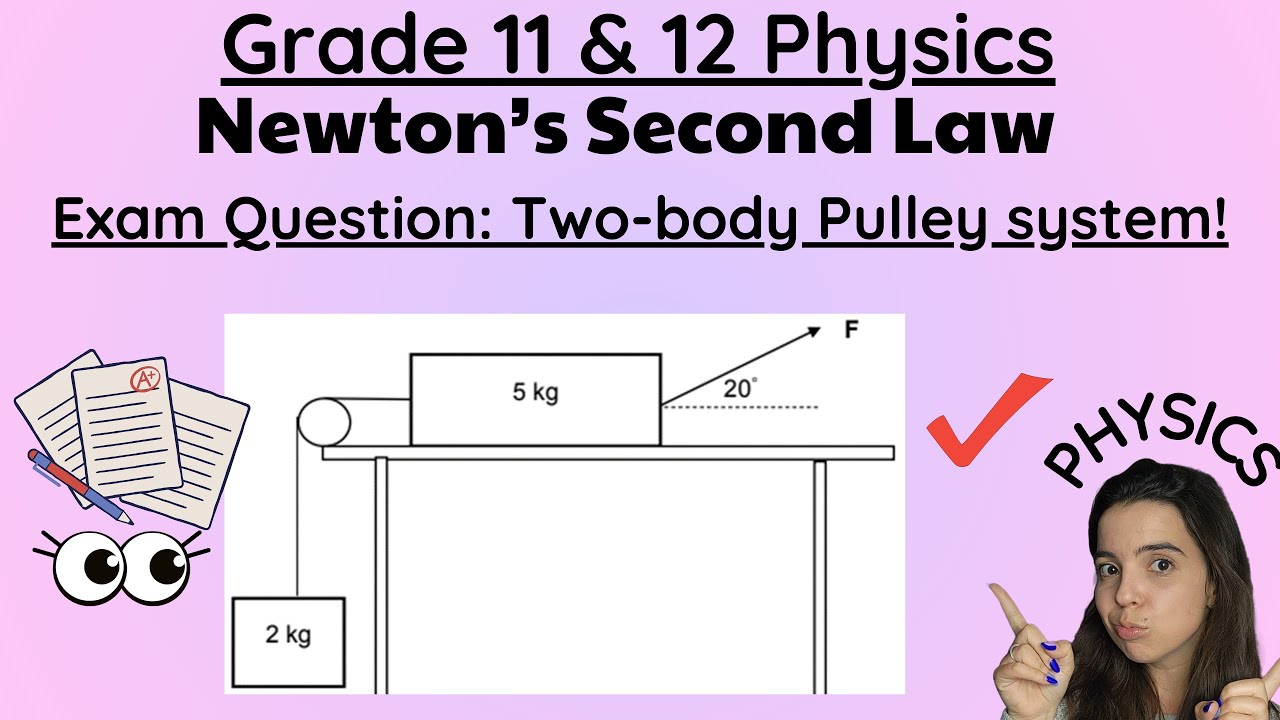
Newton's Second Law Exam Question: Two-body systems Pulley practice

AP Physics - Collisions in Multiple Dimensions

Net Force Physics Problems With Frictional Force and Acceleration

Kinetic Energy - Introductory Example Problems

AP Physics Workbook 2.K Acceleration of Systems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsPulleysMass AccelerationNewton's LawProblem SolvingEducational ContentMechanicsEngineeringScience TutorialLearning Process