Physics 53 Polarization (5 of 5) Brewster's Angle

Michel van Biezen
29 Apr 201306:26
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explores the fascinating phenomenon of light polarization at Brewster's angle. It explains how light, when incident at a specific angle on a surface with different indices of refraction, can become completely polarized. The script delves into the mathematical derivation of Brewster's angle using Snell's law and trigonometric identities, illustrating the process with an example involving air and water. The result is a clear explanation of how to calculate the angle at which light reflects and refracts to achieve polarization, concluding with the example of a 53.6-degree Brewster's angle for air to water.

Takeaways
  • 🌟 Light can be polarized through a phenomenon associated with Brewster's angle when it interacts with a surface.
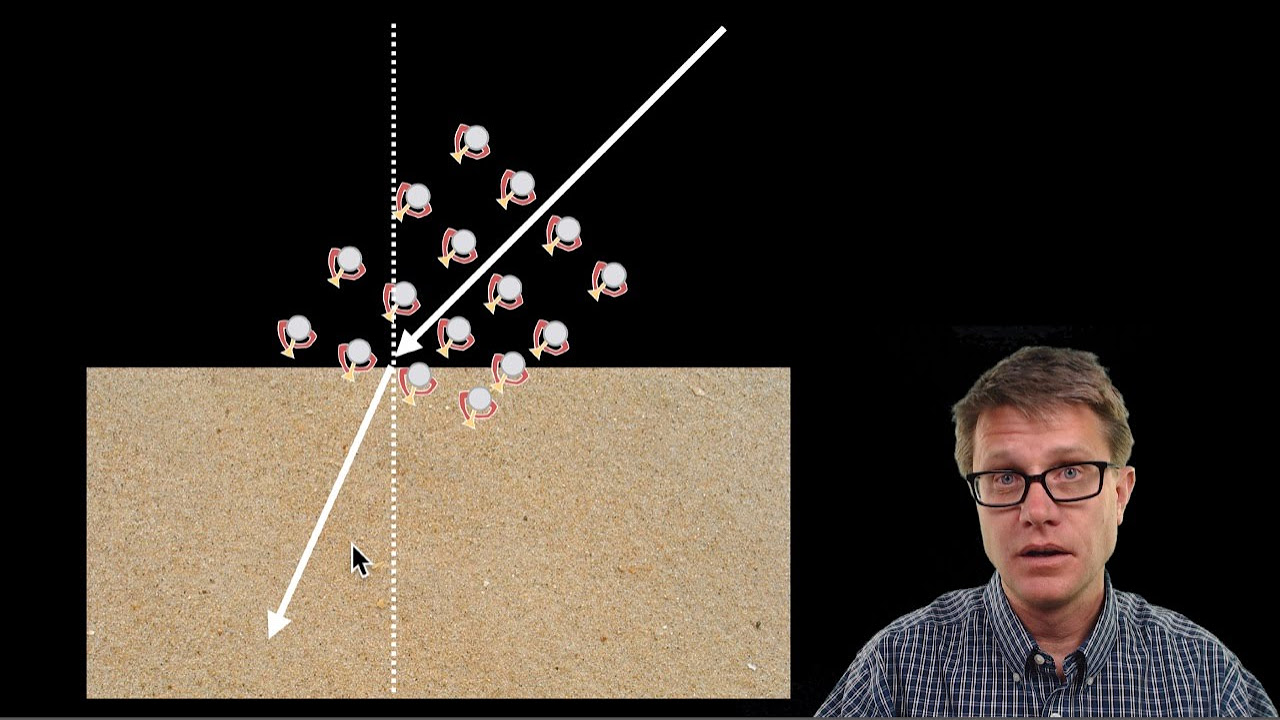
  • 🔄 Unpolarized light, when reflected off a surface, can become completely polarized at a specific angle, known as Brewster's angle, where the reflected and refracted rays are perpendicular.
  • 📐 The relationship between the angles of incidence and refraction is governed by Snell's law, which is essential in determining Brewster's angle.
  • 📉 The index of refraction (N1 and N2) plays a crucial role in the polarization process, with N1 typically representing air and N2 representing the medium like water.
  • 🔢 Brewster's angle is calculated using the tangent of the angle of incidence (Theta sub 1), which is equal to the ratio of the refractive indices (N2/N1).
  • 🧭 For air (N1 = 1) and water (N2 = 1.33), the Brewster's angle is approximately 53.6°, meaning light polarizes when incident at this angle relative to the normal.
  • 📚 Understanding Brewster's angle is important in various applications, such as in optics and the study of light polarization.
  • 📐 The normal to the surface is a key reference in visualizing and calculating the angles involved in the polarization process.
  • 📉 The angle of incidence (Theta sub 1) and the angle of refraction (Theta sub 2) are interconnected, with their sum being 180° minus the angle between the reflected and refracted rays.
  • 🔍 A trigonometric identity is used to simplify the equation derived from Snell's law, allowing for the calculation of Brewster's angle.
  • 🛠 The use of a calculator to find the arctangent of the ratio of refractive indices provides the exact Brewster's angle for given media.
Q & A

  • What is the phenomenon of light polarization associated with Brewster's angle?

    -When unpolarized light is incident at a certain angle on a reflective surface, and the angle between the reflected and refracted light is 90 degrees, the reflected light becomes completely polarized. This special angle is known as Brewster's angle.

  • What happens when light is incident on a surface with a different index of refraction?

    -Some of the light is transmitted or refracted, while some is reflected. If the refractive index of the second medium (N2) is larger than the first (N1), the angle of incidence (Theta sub 1) will be larger than the refracted angle (Theta sub 2).

  • What is the relationship between the angles of incidence and refraction according to Snell's law?

    -Snell's law states that N1 * sin(Theta sub 1) = N2 * sin(Theta sub 2), where N1 and N2 are the indices of refraction for the first and second mediums, and Theta sub 1 and Theta sub 2 are the angles of incidence and refraction, respectively.

  • How is Brewster's angle defined in terms of the incident light and the normal to the surface?

    -Brewster's angle is the angle of incidence at which the reflected light is polarized. It is the angle where the angle between the reflected and refracted rays is 90 degrees.

  • What is the significance of the angle between the reflected and refracted light being 90 degrees?

    -When this angle is 90 degrees, the reflected light is completely polarized, which is a unique property utilized in various optical applications.

  • What are the indices of refraction for air and water as mentioned in the script?

    -The index of refraction for air (N1) is approximately 1, and for water (N2), it is 1.33.

  • How can you calculate Brewster's angle using the indices of refraction?

    -You can calculate Brewster's angle by using the formula tan(Theta sub 1) = N2 / N1, where Theta sub 1 is Brewster's angle, and N1 and N2 are the indices of refraction of the two mediums.

  • What trigonometric identity is used to simplify the equation involving the sine of the angle difference in Snell's law?

    -The trigonometric identity used is sin(A - B) = sin(A)cos(B) - cos(A)sin(B), which simplifies the equation to sin(90° - Theta sub 1) = cos(Theta sub 1).

  • What is the Brewster's angle for light reflecting off a smooth water surface from air?

    -The Brewster's angle for light reflecting off a smooth water surface from air is approximately 53.6 degrees.

  • Why is a calculator needed to find Brewster's angle in the script?

    -A calculator is needed to compute the arctangent of the ratio of the refractive indices (1.33/1) to find the exact Brewster's angle.

  • What happens when light is shone at Brewster's angle on a smooth surface?

    -When light is shone at Brewster's angle on a smooth surface, the reflected light becomes polarized, with the electric field oscillating in a single plane.

Outlines
00:00
🌟 Introduction to Brewster's Angle and Light Polarization

The first paragraph introduces the concept of light polarization through Brewster's angle. It explains how light, when it strikes a surface at a certain angle, can become polarized if the angle between the reflected and refracted light is 90 degrees. The importance of the indices of refraction (N1 and N2) is highlighted, with an example given where air (N1=1) meets a water surface (N2=1.33). The paragraph sets the stage for understanding how the angle of incidence affects light polarization.

05:00
🔍 Calculating Brewster's Angle for Polarized Light

The second paragraph delves into the mathematical process of determining Brewster's angle, which is the angle at which light reflects off a surface and becomes completely polarized. It uses Snell's law and trigonometric identities to derive the formula for Brewster's angle in terms of the refractive indices of the two media involved. The specific example of light reflecting off a water surface is used to calculate the angle, resulting in Brewster's angle being approximately 53.6 degrees. This summary captures the key steps and the final result of the calculation.

Mindmap
Keywords
💡Polarization
Polarization refers to the orientation of light waves in a specific direction. In the context of the video, it is the process by which light becomes polarized when it reflects off a surface at a certain angle, known as Brewster's angle. The script discusses how light, when unpolarized, becomes completely polarized upon reflection at this angle, which is a key phenomenon in the study of light and optics.
💡Brewster's Angle
Brewster's angle is the angle of incidence at which light reflects off a surface such that the reflected light is completely polarized. Defined as the angle where the reflected and refracted rays are perpendicular to each other, it is central to the video's discussion on how light polarization occurs. The script explains how to calculate this angle using the indices of refraction for two different media, such as air and water.
💡Refraction
Refraction is the bending of light as it passes from one medium to another with a different refractive index. In the video, refraction is mentioned in the context of light passing from air into water, where the light bends due to the change in the medium's optical density. This concept is crucial for understanding how light behaves when it interacts with different materials.
💡Reflection
Reflection is the process by which light bounces off a surface. The video script describes how part of the incident light is reflected off the surface while the rest is transmitted or refracted. The angle of reflection is equal to the angle of incidence, and it plays a significant role in the polarization of light at Brewster's angle.
💡Normal
The normal is a line perpendicular to the surface at the point of incidence. In the script, the normal is used to describe the orientation of the incident, reflected, and refracted light rays. It is essential for understanding the geometric relationship between these rays and for calculating Brewster's angle.
💡Index of Refraction
The index of refraction (N) is a measure of how much light slows down in a medium compared to a vacuum. It is used in the script to differentiate between the optical densities of air (N1) and water (N2), which affects the angles of incidence and refraction, and ultimately Brewster's angle.
💡Snell's Law
Snell's Law is a formula used to predict the relationship between the angles of incidence and refraction when light passes through different media. The script uses Snell's Law to derive the condition for Brewster's angle, showing that the product of the sine of the incident angle and the index of refraction of the first medium equals the product of the sine of the refracted angle and the index of refraction of the second medium.
💡Trigonometric Identity
A trigonometric identity is a mathematical equation that equates one trigonometric expression to another. In the script, the identity sin(90° - x) = cos(x) is used to simplify the equation derived from Snell's Law, allowing for the calculation of Brewster's angle.
💡Arc Tangent
The arc tangent, or inverse tangent, is a function that returns the angle whose tangent is a given number. In the video, the arc tangent is used to solve for the Brewster's angle, by taking the inverse tangent of the ratio of the refractive indices of the two media (N2/N1).
💡Optical Density
Optical density is a measure of how much a medium can bend light, which is related to its refractive index. The script implies the concept of optical density when discussing the difference between air and water, and how this affects the polarization of light at Brewster's angle.
💡Polarizer
A polarizer is a device that filters light, allowing only light waves vibrating in a specific direction to pass through. The script mentions polarizers in the context of achieving polarized light, similar to the effect observed when light reflects at Brewster's angle.
Highlights

Introduction to the phenomenon of light polarization associated with Brewster's angle.

Explanation of how light interacts with a surface, resulting in both reflection and refraction.

Description of the relationship between the angles of incidence and refraction based on the indices of refraction.

The concept that at Brewster's angle, the reflected light becomes completely polarized.

Condition for polarization is the angle between the reflected and refracted light equals 90°.

Brewster's angle is the angle of incidence that results in polarized reflected light.

Assumption that N1 (air) equals 1 and N2 (water) equals 1.33 for the example calculation.

Use of Snell's law to relate the indices of refraction to the angles of incidence and refraction.

Derivation of Brewster's angle using trigonometric identities and Snell's law.

The tangent of the Brewster's angle is equal to the ratio of the refractive indices (N2/N1).

Calculation of Brewster's angle using the arctangent function with the refractive indices.

Result of the calculation: Brewster's angle is approximately 53.6° for air to water transition.

Practical application: When light is shone at Brewster's angle on a smooth water surface, the reflected light is polarized.

Brewster's angle's significance in optics and its role in understanding the polarization of light.

The process of deriving Brewster's angle showcases the interplay between physics and mathematics.

Brewster's angle provides a natural method for light polarization without the need for a physical polarizer.

The demonstration of Brewster's angle as an example of the practical applications of theoretical physics.

Transcripts

Browse More Related Video

Physics 52 Refraction and Snell's Law (4 of 11) Total Internal Reflection: From Water to Air

Total internal reflection | Geometric optics | Physics | Khan Academy

Refraction of Light

Total Internal Reflection of Light and Critical Angle of Refraction Physics

Physics 52 Refraction and Snell's Law (9 of 11) Ex. 4: Light Through a Prism

Refraction of Light

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PolarizationBrewster's AngleLight ReflectionOpticsPhysicsRefractionSnell's LawTrigonometrySurface BoundaryEducational