Total internal reflection | Geometric optics | Physics | Khan Academy
TLDRThis educational script explains the concept of light refraction and total internal reflection using the analogy of a car transitioning from mud to a road. It introduces Snell's Law to determine the critical angle at which light traveling from water to air no longer refracts but reflects back, with a practical example calculating the critical angle for water as 48.8 degrees. The script also touches on the application of this principle in fiber-optic cables, where light is internally reflected to transmit information.
Takeaways
- 🌟 Light exiting a slow medium to a fast medium bends towards the normal due to a change in speed, similar to a car moving from mud to a road.
- 🔍 The angle of refraction (θ2) is always greater than the angle of incidence (θ1) when light moves from a slower to a faster medium.
- 🤔 The concept of total internal reflection is introduced, where light does not escape into the fast medium but reflects back into the slow medium at angles greater than a critical angle (θ3).
- 🔢 The critical angle (θ critical) is the angle of incidence at which the angle of refraction becomes 90 degrees, and no light escapes the slow medium.
- 📚 Snell's Law is used to calculate the critical angle, relating the indices of refraction of the two media and the angles of incidence and refraction.
- 🌊 The example of light traveling from water (index of refraction 1.33) to air (approximated as 1.00) is used to illustrate the calculation of the critical angle.
- 📉 At the critical angle, the sine of the refraction angle (which is 90 degrees) is 1, simplifying the calculation of the critical angle using Snell's Law.
- 📐 The critical angle for light traveling from water to air is calculated to be approximately 48.8 degrees.
- 🚫 If the angle of incidence is greater than the critical angle, total internal reflection occurs, and the light does not refract but reflects back into the water.
- 🌐 The principle of total internal reflection is utilized in fiber-optic cables to transmit light signals over long distances with minimal loss.
- 👓 The script aims to make the complex physics of light refraction and total internal reflection accessible and interesting to the audience.
Q & A
What is the phenomenon described when light exits from a slow medium to a fast medium?
-The phenomenon described is refraction, where the light changes direction as it moves from a slower medium like mud to a faster one like a road, causing the light to bend towards the normal line.
What is the analogy used to explain the direction change of light when it moves from a slow to a fast medium?
-The analogy used is a car moving from mud to a road, where the left tires get out of the mud before the right tires, causing the car to veer to the right.
Why is the angle of refraction (theta 2) greater than the angle of incidence (theta 1) when light moves from a slow to a fast medium?
-According to Snell's Law, the angle of refraction is greater than the angle of incidence when light travels from a denser medium to a less dense medium because the light speeds up and bends away from the normal line.
What is the critical angle and why is it significant?
-The critical angle is the angle of incidence at which the angle of refraction becomes 90 degrees. It is significant because beyond this angle, light undergoes total internal reflection and does not escape into the fast medium.
What is total internal reflection and how does it occur?
-Total internal reflection is a phenomenon where light is completely reflected back into the medium from which it originated, rather than refracting into another medium. It occurs when the angle of incidence exceeds the critical angle.
How is Snell's Law applied to determine the critical angle for light traveling from water to air?
-Snell's Law is applied by setting the sine of the critical angle equal to the ratio of the refractive indices of the two media, with the sine of the refraction angle set to 1 (since it's 90 degrees). The critical angle is then found by taking the inverse sine of the refractive index ratio.
What is the refractive index of water and air as mentioned in the script?
-The refractive index of water is given as 1.33, and for simplicity, the refractive index of air is approximated as 1.00.
How is the critical angle calculated for light traveling from water to air?
-The critical angle is calculated by taking the inverse sine of the ratio of the refractive index of air (1.00) to that of water (1.33), which results in a critical angle of approximately 48.8 degrees.
What happens to light when the angle of incidence is less than the critical angle?
-When the angle of incidence is less than the critical angle, light refracts and escapes into the fast medium, following the laws of refraction.
What happens to light when the angle of incidence is equal to the critical angle?
-At the critical angle, the angle of refraction is 90 degrees, meaning the light travels along the surface of the boundary between the two media without escaping into the fast medium.
How do fiber-optic cables utilize the principle of total internal reflection?
-Fiber-optic cables work by guiding light along their length through total internal reflection. The light is kept within the glass or plastic core of the cable, reflecting internally at angles greater than the critical angle.
Outlines
🌟 Light Refraction and Total Internal Reflection
This paragraph introduces the concept of light refraction using an analogy of a car transitioning from a slow medium (mud) to a fast one (road), illustrating how the direction of the light changes as it exits a slow medium. It poses the question of whether there's a critical angle at which the light's refraction angle becomes 90 degrees, preventing the light from escaping into the fast medium. This phenomenon is known as total internal reflection. The paragraph sets the stage for an exploration of the critical angle and its significance in the behavior of light when moving from one medium to another.
🔍 Calculating the Critical Angle Using Snell's Law
The second paragraph delves into the mathematical calculation of the critical angle using Snell's Law. It explains how to determine the angle at which light will no longer refract but will instead undergo total internal reflection. The example uses water with an index of refraction of 1.33 and air with an approximate index of 1.00. The critical angle is calculated by setting up an equation where the sine of the refraction angle (90 degrees) is equated to the ratio of the indices of refraction. The sine of the critical angle is found to be 1/1.33, and taking the inverse sine gives a critical angle of 48.8 degrees. This means that any light exiting water at an incident angle greater than 48.8 degrees will reflect back into the water instead of refracting into the air. The paragraph concludes with an application of this concept in fiber-optic cables, where light is kept within the cable by maintaining incident angles greater than the critical angle.
Mindmap
Keywords
💡Light
💡Refraction
💡Incident Angle
💡Angle of Refraction
💡Critical Angle
💡Total Internal Reflection
💡Snell's Law
💡Index of Refraction
💡Unit Circle
💡Fiber-Optic Cables
Highlights
Light exiting a slow medium and the analogy of a car transitioning from mud to road to explain refraction.
The concept of refraction angle being greater than the incident angle when moving from a slow to a fast medium.
Introduction of the critical angle, theta 3, where the refracted angle equals 90 degrees, indicating light cannot escape the medium.
Total internal reflection occurs when the incident angle is larger than the critical angle, causing light to reflect back into the slow medium.
The use of Snell's Law to determine the critical angle for light transitioning between two media.
The calculation of the critical angle using the indices of refraction for water and air.
The critical angle for light exiting water is calculated to be 48.8 degrees.
Practical application of the critical angle in fiber-optic cables, where light is kept within the cable through total internal reflection.
The importance of the unit circle in determining the sine of 90 degrees for the calculation of the critical angle.
The inverse sine function's role in finding the critical angle from the ratio of indices of refraction.
The significance of the indices of refraction in determining the behavior of light at the interface between two media.
The practical demonstration of calculating the critical angle using a TI-85 calculator.
The theoretical underpinning of why the refraction angle is always larger when light moves from a denser to a less dense medium.
The explanation of how light behaves at the critical angle, traveling along the surface of the medium.
The analogy of light behaving like a car to simplify the understanding of refraction and total internal reflection.
The educational value of the video in explaining complex optical phenomena in an accessible manner.
Transcripts
Browse More Related Video
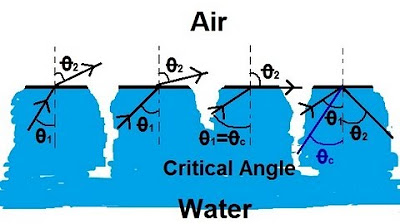
Physics 52 Refraction and Snell's Law (4 of 11) Total Internal Reflection: From Water to Air
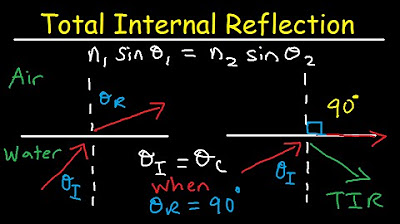
Total Internal Reflection of Light and Critical Angle of Refraction Physics
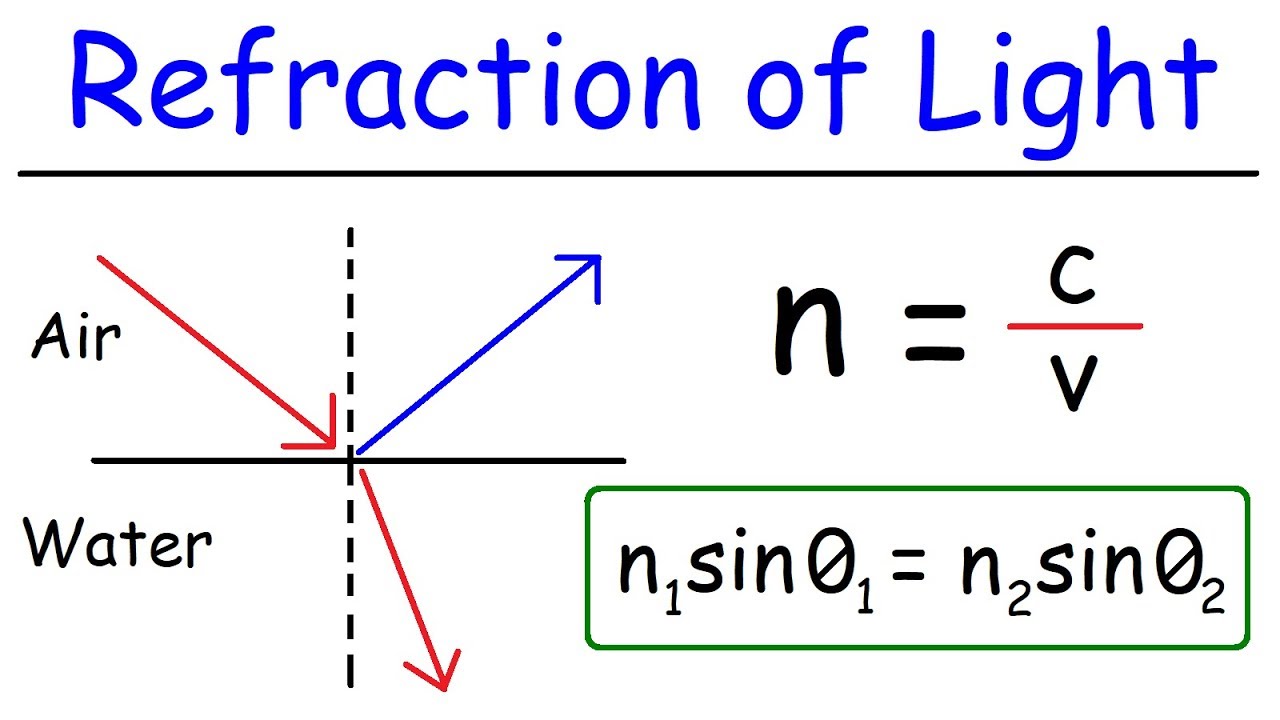
Refraction of Light
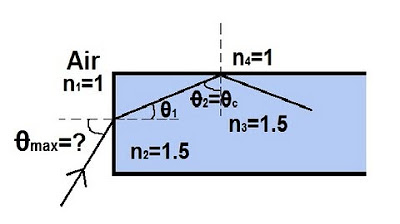
Physics 52 Refraction and Snell's Law (5 of 11) The Fiber Optic Cable
Refraction of Light
Physics 53 Polarization (5 of 5) Brewster's Angle
5.0 / 5 (0 votes)
Thanks for rating: