How to Read a T-Table and Z-Table

Learn2Stats
14 Feb 202206:37
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script offers a clear guide on interpreting z-tables and t-tables for statistical analysis. It emphasizes the z-table's intuitiveness, explaining how to find probabilities associated with z-scores and critical values. The script then contrasts this with the t-table, which involves degrees of freedom and requires comparing calculated t-scores to critical values for hypothesis testing. The explanation includes finding confidence intervals and understanding one-tailed versus two-tailed tests, aiming to clarify common confusions and enhance statistical literacy.

Takeaways
  • 📚 The video is a tutorial on how to read Z-tables and T-tables in statistics.
  • 🔍 The presenter finds Z-tables more intuitive than T-tables due to their simpler structure without degrees of freedom.
  • 🎯 Z-tables directly associate critical values with probabilities and vice versa.
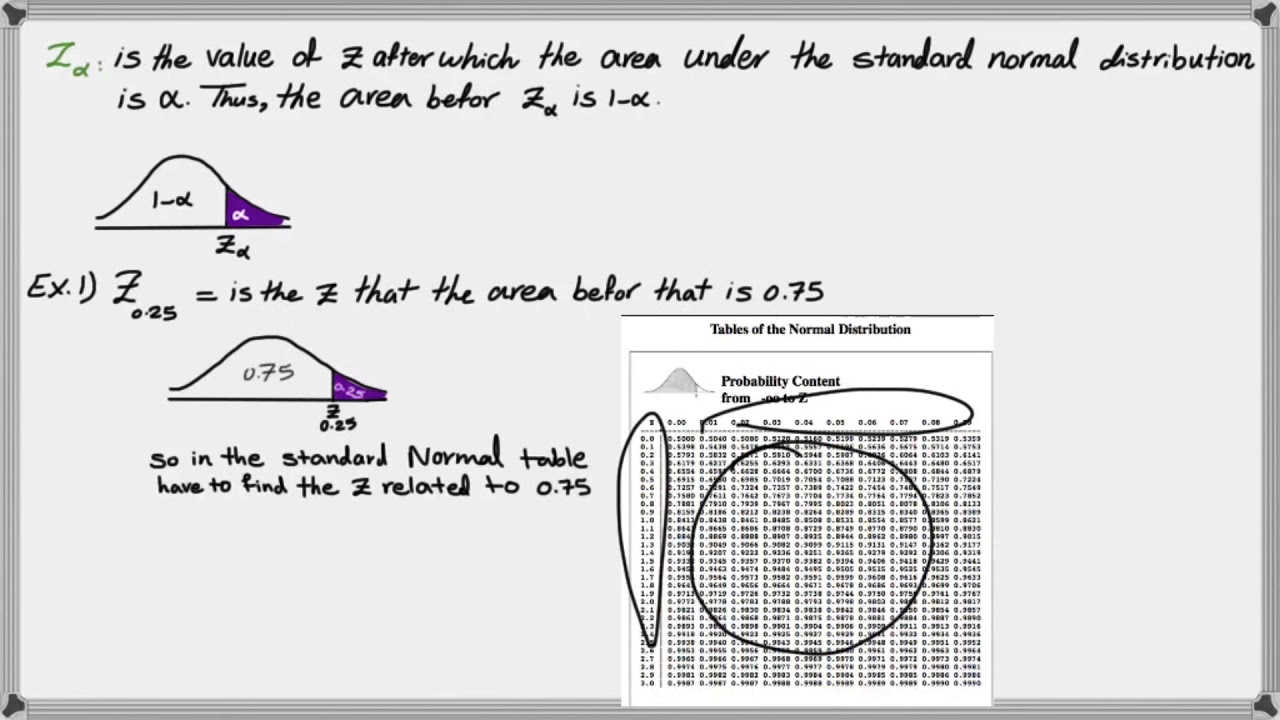
  • 📊 To read a Z-score in the table, locate the score on the table and find the intersecting probability.
  • 🔢 For a Z-score of 1.32, the probability is approximately 0.9066.
  • 🔍 To find the critical value for a given probability, locate the probability in the table and identify the corresponding Z-score.
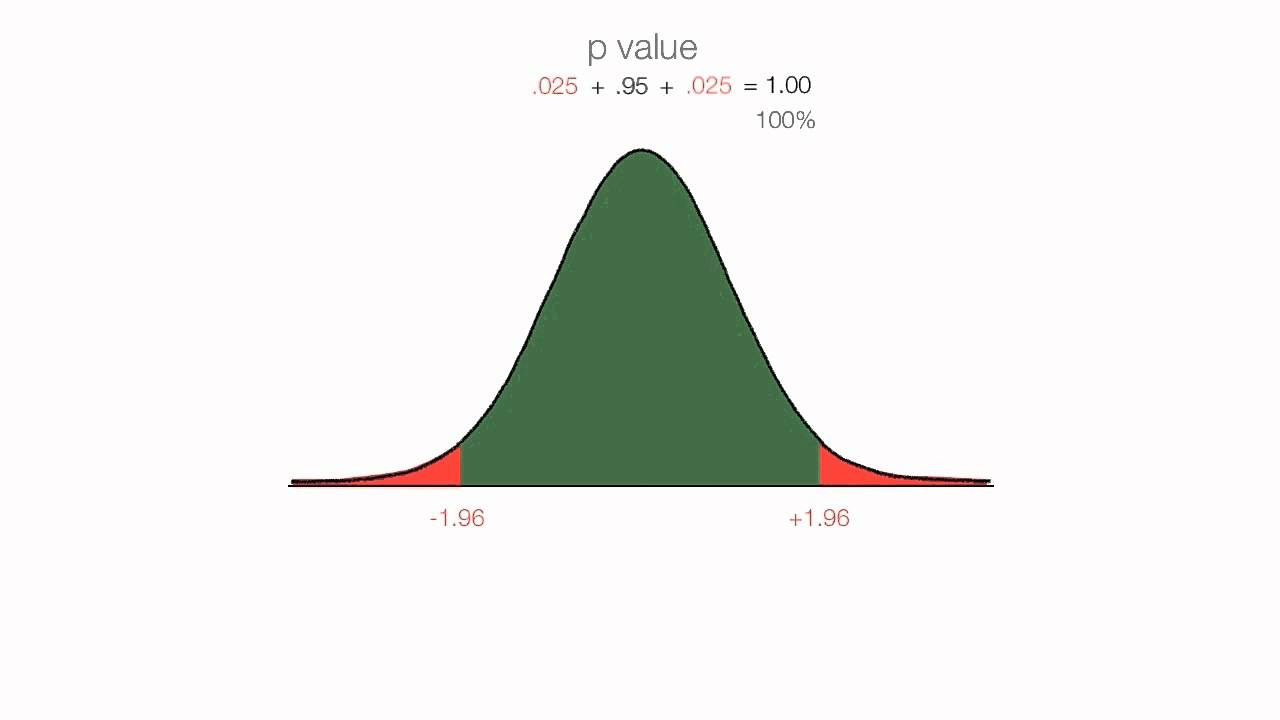
  • 🌐 Understanding the symmetry of the normal distribution helps in finding the reverse probability by using one minus the given probability.
  • 📉 For a 95% confidence interval, the critical Z-value is approximately 1.645, found by averaging the values at 0.9495 and 0.9505.
  • ➡️ The negative of a Z-score represents the lower tail of the distribution, useful for one-tailed confidence intervals.
  • 📈 T-tables are more complex due to the inclusion of degrees of freedom and are used to find critical values for hypothesis testing.
  • 🔑 T-tables do not directly provide probabilities; they are used to compare calculated t-scores with critical values for significance testing.
  • 📚 The presenter suggests that understanding Z-tables can make learning T-tables easier, despite the common teaching order being the reverse.
Q & A

  • What are the two main types of statistical tables discussed in the script?

    -The script discusses how to read a Z-table and a T-table, which are used for normal distribution and t-distribution respectively.

  • Why does the speaker find the Z-table more intuitive than the T-table?

    -The speaker finds the Z-table more intuitive because it does not involve degrees of freedom and directly associates critical values with probabilities.

  • What is a Z-score and how is it used in the context of the script?

    -A Z-score is a standard score that indicates how many standard deviations an element is from the mean. In the script, a Z-score of 1.32 is used to demonstrate how to read probabilities from the Z-table.

  • How does the script explain finding the probability associated with a Z-score?

    -The script explains that you look at the table to find the closest Z-score value, and then find the corresponding probability to the left of that value, as the table is reflective of the area to the left of the critical value.

  • What is the probability associated with a Z-score of 1.32 according to the script?

    -The probability associated with a Z-score of 1.32 is approximately 0.9066, as explained in the script.

  • How does the script describe finding the critical value for a given probability?

    -The script describes finding the critical value by looking through the probabilities in the table and identifying the value that corresponds to the desired probability, such as 0.9495 and 0.9505 for a 95% probability.

  • What critical value is commonly used for a 95% probability in the Z-table?

    -The critical value commonly used for a 95% probability is 1.645, which is the average of the two probabilities 0.9495 and 0.9505.

  • How does the script explain the concept of a one-tailed and two-tailed test in the context of the T-table?

    -The script explains that a one-tailed test focuses on one side of the distribution (either greater than or less than), while a two-tailed test considers both sides. The critical value for a one-tailed test is found by looking at the 0.025 level, whereas for a two-tailed test, it's the middle 95%.

  • What is the difference between using the Z-table and the T-table when calculating a confidence interval?

    -The Z-table directly provides probabilities, making it easier to calculate confidence intervals, while the T-table provides critical values that need to be compared with calculated t-scores, and probabilities are not directly available without additional tools or software.

  • How does the script suggest finding the negative critical value for a confidence interval?

    -The script suggests that to find the negative critical value, you simply put a negative sign in front of the positive critical value because the normal distribution is symmetrical.

  • What does the script imply about the importance of understanding the symmetry of the normal distribution when using the Z-table?

    -The script implies that understanding the symmetry of the normal distribution is crucial when using the Z-table because it allows you to easily find the corresponding probability for the negative side of the distribution by using the one minus the positive probability.

Outlines
00:00
📊 Understanding Z-Tables for Probabilities

This paragraph introduces the concept of reading a Z-table to determine probabilities associated with a given Z-score. The speaker explains that Z-tables are more intuitive than T-tables due to their straightforward critical values and lack of degrees of freedom. The process of finding the probability for a Z-score of 1.32 is demonstrated, showing how to locate the score on the table and interpret the resulting probability of 0.9066. Additionally, the paragraph covers how to find the critical value for a specific probability, using the example of a 95% probability with a critical value of 1.645. The importance of symmetry in the normal distribution is highlighted, and the concept of negative Z-scores is briefly introduced.

05:01
🔍 Transitioning from Z-Tables to T-Tables

The second paragraph discusses the transition from Z-tables to T-tables, emphasizing the additional complexity of T-tables due to the inclusion of degrees of freedom. The speaker clarifies that T-tables are used to find critical values rather than direct probabilities, which often require the use of software or online calculators. The paragraph explains how to interpret T-tables for both one-tailed and two-tailed tests, using the example of a T-table with 2 degrees of freedom and a 95% probability, which corresponds to a critical value of 4.303 for a two-tailed test and 2.92 for a one-tailed test. The speaker also shares personal insights on the learning process, suggesting that starting with Z-tables before moving to T-tables can be less confusing for beginners. The paragraph concludes with an invitation for feedback and a parting message encouraging viewers to stay curious.

Mindmap
Keywords
💡Z Table
A Z table, also known as a standard normal distribution table, is used to find probabilities associated with Z-scores. In the video, the Z table is described as more intuitive than the T table due to its straightforward association between critical values and probabilities. The script uses the Z table to illustrate how to find the probability associated with a Z-score of 1.32, highlighting the table's symmetry and how to interpret the probabilities for both positive and negative Z-scores.
💡Critical Value
In statistics, a critical value is the value of a test statistic that separates the region where the null hypothesis is rejected from the region where it is not rejected. The video explains how to find critical values using the Z table and how they are associated with specific probabilities. For instance, a Z-score of 1.645 is identified as the critical value for a 95% confidence interval, demonstrating its importance in hypothesis testing.
💡Probability
Probability is a measure of the likelihood that a given event will occur. The video script discusses how to read probabilities from the Z table and how they relate to critical values. It also explains how to find the critical value when the desired probability is known, such as finding the Z-score that corresponds to a 95% probability.
💡Degrees of Freedom
Degrees of freedom in statistics refer to the number of values in the calculation that are free to vary. The script mentions that the T distribution, unlike the Z distribution, takes into account degrees of freedom, which affects the shape of the distribution and thus the critical values for hypothesis testing.
💡T Table
A T table is used to find critical values for the T distribution, which is used in hypothesis testing when the population standard deviation is unknown and the sample size is small. The video contrasts the T table with the Z table, noting that the T table includes degrees of freedom and is used to compare calculated T-scores with critical values.
💡Normal Distribution
The normal distribution, also known as Gaussian distribution, is a probability distribution that is symmetrical and defined by its mean and standard deviation. The video emphasizes the symmetry of the normal distribution when explaining how to interpret probabilities and critical values from the Z table.
💡Confidence Interval
A confidence interval is a range of values, derived from a data sample, that is likely to contain the value of an unknown population parameter. The script explains how to use the Z table to find the critical values that define a 95% confidence interval, which is a key concept in inferential statistics.
💡Hypothesis Test
A hypothesis test is a statistical method used to evaluate whether there is enough evidence against the null hypothesis. The video script discusses how critical values from the T table are used in hypothesis testing to compare with calculated T-scores to determine if the null hypothesis should be rejected.
💡P-Value
The p-value is the probability of obtaining results at least as extreme as the observed results, assuming that the null hypothesis is true. The script mentions that finding the p-value typically requires the use of statistical software or online calculators, as it is not directly available from the T table.
💡Symmetric
Symmetry in the context of the normal distribution means that the distribution is mirror-imaged across its mean. The video uses the concept of symmetry to explain how to find probabilities for negative Z-scores by using the one minus the probability of the positive Z-score.
💡One-Tailed and Two-Tailed Tests
One-tailed and two-tailed tests refer to the directionality of a hypothesis test. A one-tailed test assesses whether a value is greater than or less than a certain value, while a two-tailed test assesses whether a value is different from a certain value in either direction. The script explains how to find the critical values for both one-tailed and two-tailed tests using the T table.
Highlights

Introduction to reading a Z table and a T table for statistical analysis.

Z table is considered more intuitive due to the absence of degrees of freedom.

Explanation of associating critical values with probabilities in Z tables.

Demonstration of how to read a Z-score of 1.32 on the table.

Understanding the symmetry of the normal distribution for probability calculations.

Finding the critical value for a 95% probability using the Z table.

Calculating the negative Z-score for a 90% confidence interval.

Differences between Z and T tables, particularly the inclusion of degrees of freedom in T tables.

The process of finding a critical value in T tables for a given probability.

Using software to find probabilities in T tables due to their complexity.

Explanation of comparing calculated t-scores with critical t-values in hypothesis testing.

Differentiating between one-tailed and two-tailed tests in hypothesis testing.

Finding the critical t-value for a specific degree of freedom and probability.

The importance of hypothesis in determining whether to use one-tailed or two-tailed tests.

Teaching preference and the transition from Z to T tables in learning statistics.

Invitation for feedback on the video to improve future content.

Closing remarks encouraging viewers to stay engaged with the material.

Transcripts

Browse More Related Video

P Values, z Scores, Alpha, Critical Values

Elementary Statistics - Chapter 8 - Hypothesis Testing Part 3 Revised

Hypothesis Testing - Solving Problems With Proportions

Student's t-test

How to find critical Z value (Z alpha)

Find a pvalue using a t table

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsZ-TableT-TableCritical ValuesProbabilityConfidence IntervalsHypothesis TestingEducationalTutorialData AnalysisStatistical Distributions