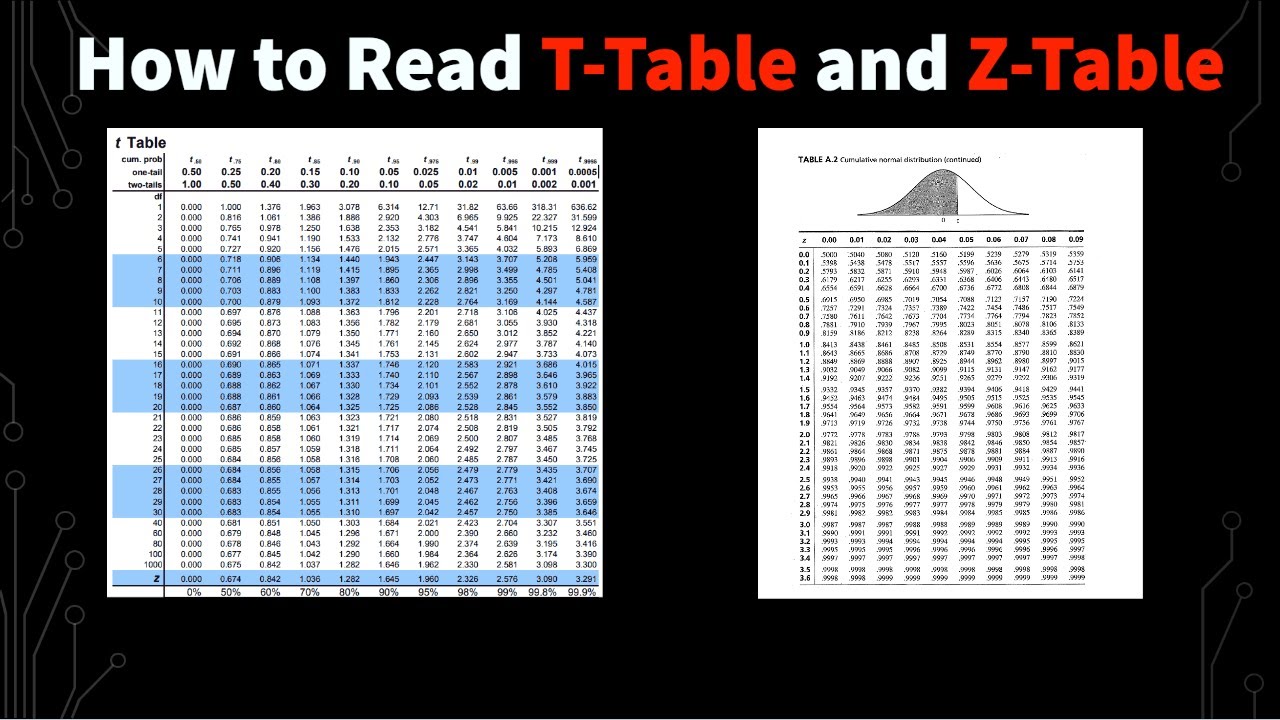
Find a pvalue using a t table
TLDRThis educational video demonstrates how to utilize a t-table to determine p-values for t-procedures. It explains the process of identifying the degrees of freedom and the test statistic, then locating these on the t-table to find the corresponding p-value range. The video illustrates examples with varying degrees of freedom and test statistics, showing how to interpret results when the statistic exceeds table limits or when degrees of freedom are not explicitly listed. It emphasizes the importance of understanding one-tailed and two-tailed tests for accurate p-value determination.
Takeaways
- 📊 A t-table is used to find p-values for t-procedures after calculating the degrees of freedom and test statistic.
- 🔍 The process of finding a p-value is consistent across different types of t-tests, such as one-sample t-tests.
- 🔢 Degrees of freedom are used to locate the correct row on the t-table.
- 🔍 The absolute value of the test statistic is used to find its position on the t-table, regardless of its sign.
- 📉 For a test statistic that falls between two values on the t-table, the p-value is estimated to be between the corresponding p-values on the table.
- 🚫 If the test statistic exceeds the highest value on the t-table, the p-value is less than the smallest p-value listed.
- 📉 For large degrees of freedom not listed on the t-table, always round down to the nearest available degree of freedom.
- 🔑 The p-value for a two-tailed test is double that of a one-tailed test.
- 📝 Understanding the difference between one-sided and two-sided tests is crucial for correct interpretation of results.
- 🎯 The video aims to educate viewers on the method of finding p-values using a t-table for statistical analysis.
Q & A
What is the purpose of the video?
-The purpose of the video is to demonstrate how to use a t-table to find a p-value for any t-procedure after calculating the degrees of freedom and the test statistic.
What is a t-table used for in statistics?
-A t-table is used to determine the p-value for a t-procedure, which can be used in various statistical tests such as one-sample t-tests or other t-tests.
What are the two key components needed to find a p-value using a t-table?
-The two key components needed are the degrees of freedom and the test statistic.
Why do we use the absolute value of the test statistic when using a t-table?
-We use the absolute value of the test statistic because t-tables typically list positive values, and it ensures the correct p-value is found regardless of the original direction of the test statistic.
What does it mean if the test statistic falls between two values on the t-table?
-If the test statistic falls between two values, it means that the p-value will fall between the corresponding p-values for those two values on the t-table.
What is the implication if the test statistic is larger than the largest value on the t-table?
-If the test statistic is larger than the largest value on the t-table, it implies that the p-value is less than the smallest p-value listed on the table.
How do you determine the p-value for a one-tailed test if the test statistic is off the table?
-For a one-tailed test, if the test statistic is off the table, the p-value is less than the smallest p-value indicated on the table, which is typically less than 0.0005.
What is the difference between a one-tailed and a two-tailed test in terms of p-value interpretation?
-A one-tailed test considers the p-value in one direction (either less than or greater than), while a two-tailed test considers the p-value in both directions, effectively doubling the p-value for the same test statistic.
What should you do if the degrees of freedom are not listed on the t-table?
-If the degrees of freedom are not listed, you should round down to the nearest available degree of freedom on the t-table, as the table cannot list all possible degrees of freedom.
How does rounding down the degrees of freedom affect the p-value calculation?
-Rounding down the degrees of freedom ensures that you are using a conservative estimate, which means the p-value calculated will be slightly larger than if the exact degrees of freedom were used.
Why is it important to understand when to use a one-sided or two-sided test?
-Understanding when to use a one-sided or two-sided test is important because it affects the interpretation of the p-value and the conclusions drawn from the statistical analysis.
Outlines
📊 Understanding T-Tables for P-Value Calculation
This paragraph introduces the concept of using a t-table to determine p-values for t-procedures. It explains that once the degrees of freedom and the test statistic are calculated, the method for finding the p-value remains consistent across different types of t-tests. The paragraph provides a step-by-step guide on how to locate the appropriate row for the degrees of freedom and how to find the p-value by comparing the absolute value of the test statistic to the values on the t-table.
🔍 Locating P-Values with Degrees of Freedom and Test Statistic
The paragraph demonstrates how to use a t-table with an example where the degrees of freedom are 12 and the test statistic is -2.46. It details the process of finding the degrees of freedom row, using the absolute value of the test statistic to locate its position on the table, and then interpreting the p-value based on where the test statistic falls between the table values. The example clarifies that if the test statistic is between two values, the p-value for a one-tailed test falls between 0.01 and 0.025, and for a two-tailed test, it falls between 0.02 and 0.05.
📈 Dealing with Test Statistics Off the T-Table
This part of the script addresses the scenario where the test statistic is larger than the highest value on the t-table, using an example with 30 degrees of freedom and a test statistic of 5.69. It explains that if the test statistic exceeds the table's range, the p-value is less than the smallest p-value listed on the table, which for a one-tailed test is less than 0.0005 and for a two-tailed test is less than 0.001.
🧩 Handling Degrees of Freedom Not Listed on the T-Table
The final example in the script discusses what to do when the degrees of freedom, such as 68 in this case, are not directly listed on the t-table. It advises to always round down to the nearest listed degree of freedom, in this case, 60, because the t-table cannot list all possible degrees of freedom. The paragraph then illustrates how to find the p-value for a test statistic of 1.83 by using the 60 degrees of freedom row and explains that the p-value for a one-tailed test would be between 0.05 and 0.025, and for a two-tailed test, it would be between 0.05 and 0.10.
Mindmap
Keywords
💡t-table
💡p-value
💡degrees of freedom
💡test statistic
💡one-sample t-test
💡t-procedure
💡one-tailed procedure
💡two-tailed procedure
💡absolute value
💡round down
Highlights
This video demonstrates how to use a t-table to find p-values for any t-procedure after calculating the degrees of freedom and test statistic.
The method applies to one-sample t-tests and other types of t-procedures.
For an example with 12 degrees of freedom and a test statistic of -2.46, find the row for 12 and locate the absolute value of the test statistic on the t-table.
The p-value for this example falls between 0.01 and 0.025 for a one-tailed test, and 0.02 to 0.05 for a two-tailed test.
If the test statistic is larger than the table's maximum value, the p-value is less than the smallest p-value listed.
For a test statistic of 5.69 with 30 degrees of freedom, the p-value is less than 0.0005 for one-tailed and less than 0.001 for two-tailed tests.
When degrees of freedom are not listed on the t-table, round down to the nearest available value, like going from 68 to 60.
For 68 degrees of freedom and a test statistic of 1.83, the p-value is between 0.025 and 0.05 for one-tailed, and 0.05 and 0.10 for two-tailed tests.
The two-tailed p-value is simply double the one-tailed p-value.
Understanding when to use one-sided or two-sided tests is crucial.
The t-table method simplifies finding p-values for various t-procedures.
All t-procedures use the same approach to find p-values using the t-table.
The absolute value of the test statistic is used when locating it on the t-table.
The t-table does not list all degrees of freedom, requiring rounding down for larger values.
The video provides clear examples demonstrating the t-table method for finding p-values.
The video aims to help viewers understand and apply the t-table method for p-value calculation.
The video concludes by emphasizing the importance of knowing when to use one-sided or two-sided tests.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: