Elementary Statistics - Chapter 8 - Hypothesis Testing Part 3 Revised

Joan DeRosa

12 Nov 201746:05

EducationalLearning

32 Likes 10 Comments

TLDRThis script offers an in-depth review of hypothesis testing, focusing on the nature of tests, types of hypotheses, and the rejection region determined by the alternative statement. It explains the t-test for a mean when the population standard deviation is unknown, detailing the process of finding critical values and test statistics using alpha levels and degrees of freedom. The script also covers how to use calculators and tables for hypothesis testing, including examples of left-tail, right-tail, and two-tailed tests, ultimately guiding users on how to interpret results and make decisions based on statistical evidence.

Takeaways

📚 Hypothesis testing involves evaluating statistical claims using a null hypothesis (H0) and an alternative hypothesis (H1).
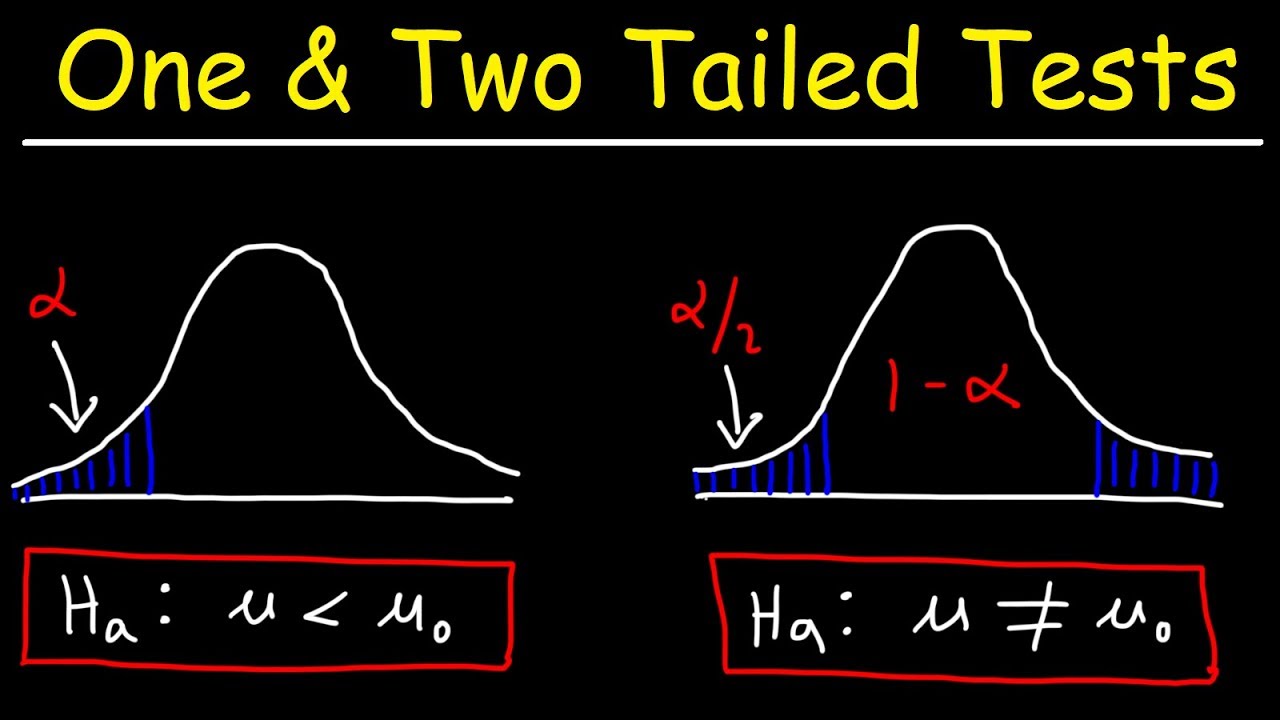
📉 In a left-tail test, the rejection region is to the left of the critical value, indicated by the alternative hypothesis with a 'less than' symbol.
📈 Right-tail tests have a rejection region to the right of the critical value, corresponding to an alternative hypothesis with a 'greater than' symbol.
🔍 The two-tailed test considers rejection regions on both sides of the distribution, used when the alternative hypothesis is 'not equal to'.
🎯 The critical value is determined by the level of significance (alpha), which is the probability of rejecting the null hypothesis when it is true.
⚖️ The t-test is used for hypothesis testing of a mean when the population standard deviation is unknown, applicable for normally distributed populations or samples larger than 30.
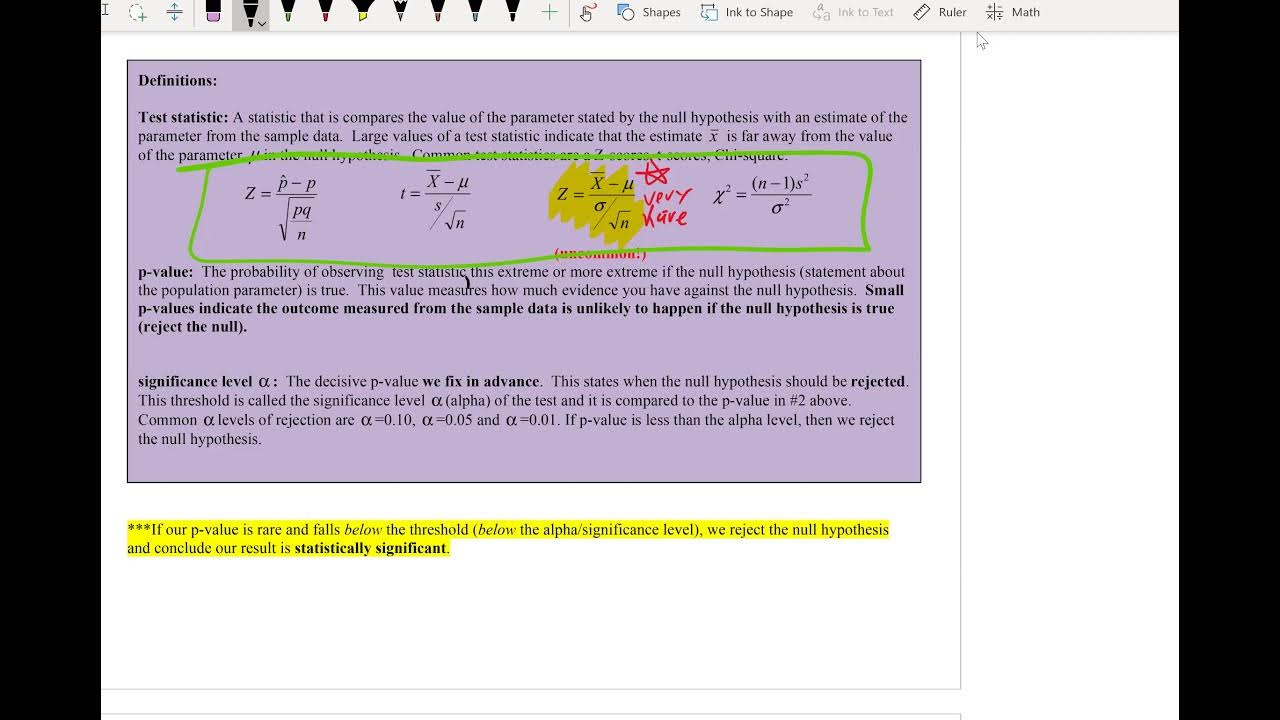
📊 To find the critical value for a t-test, identify alpha, calculate degrees of freedom (sample size - 1), and use a t-distribution table or calculator.
📘 The standardized test statistic (t-value) is compared against the critical value to decide whether to reject or fail to reject the null hypothesis.
🔢 For a t-test, the test statistic is calculated using the formula involving the sample mean, population mean, sample standard deviation, and sample size.
📝 When using a calculator for t-test, input the necessary values including mean, standard deviation, sample size, and select the correct alternative hypothesis.
🌐 The process of hypothesis testing for proportions involves the z-test, which requires conditions based on the binomial distribution to be met.

Q & A

What are the three types of hypotheses in hypothesis testing?
-The three types of hypotheses in hypothesis testing are the null hypothesis (H0), the alternative hypothesis (H1 or Ha), and sometimes the research hypothesis. The null hypothesis typically represents the status quo or a statement of no effect, while the alternative hypothesis represents the claim or research question being tested.
What is the significance of the rejection region in hypothesis testing?
-The rejection region is the area under the probability distribution curve that defines the range of values for which the null hypothesis will be rejected. It is determined based on the critical value and the level of significance (alpha), and it indicates the threshold for statistical significance.
What is the difference between a left-tail test and a right-tail test in terms of the alternative hypothesis and the rejection region?
-A left-tail test has an alternative hypothesis with a less than symbol (<), and the rejection region is the shaded area to the left of the critical value. A right-tail test has an alternative hypothesis with a greater than symbol (>), and the rejection region is the shaded area to the right of the critical value.
What is the purpose of the critical value in hypothesis testing?
-The critical value is the threshold value determined by the level of significance (alpha) that separates the rejection and non-rejection regions. If the test statistic falls into the rejection region, the null hypothesis is rejected based on the critical value.
When is the t-test for a mean used in hypothesis testing?
-The t-test for a mean is used in hypothesis testing when the population standard deviation is unknown and the population is normally distributed or the sample size is greater than or equal to 30.
What is the formula used to calculate the standardized test statistic in a t-test for a mean?
-The formula for the standardized test statistic (t) in a t-test for a mean is t = (Sample Mean - Population Mean) / (Sample Standard Deviation / √Sample Size).
How do you determine the critical value for a t-test using a calculator?
-To determine the critical value for a t-test using a calculator, you would typically use the inverse T function, entering the level of significance (alpha) and the degrees of freedom, and then pressing enter to obtain the critical value.
What is the difference between a one-tailed test and a two-tailed test in terms of the rejection region?
-A one-tailed test has a rejection region on either the extreme left or right side of the distribution curve, depending on whether the alternative hypothesis is less than or greater than, respectively. A two-tailed test has rejection regions on both tails of the distribution, and the test statistic can reject the null hypothesis if it falls into either of the two shaded regions.
What is the role of the sample size in determining the degrees of freedom in a t-test?
-The degrees of freedom in a t-test is determined by the sample size minus one (n - 1). It is used to find the critical value from the t-distribution table or calculator, which in turn is used to determine the rejection region.
How do you interpret the results of a hypothesis test in the context of the original claim?
-After conducting the hypothesis test, if the test statistic falls into the rejection region, you reject the null hypothesis, which means there is enough evidence to support the alternative hypothesis and the original claim. If the test statistic does not fall into the rejection region, you fail to reject the null hypothesis, indicating there is not enough evidence to support the claim.

Outlines

00:00

📚 Hypothesis Testing Review

This paragraph reviews the basics of hypothesis testing, explaining the nature of tests, types of hypotheses, and the concept of rejection regions based on the alternative hypothesis. It delves into left-tail, right-tail, and two-tailed tests, highlighting the role of the critical value derived from the level of significance (alpha). The paragraph also introduces the t-test for a mean when the population standard deviation is unknown, discussing its conditions of use and the formula for the standardized test statistic.

05:01

📉 T-test Calculation and Rejection Regions

The paragraph focuses on calculating the t-test for a mean, emphasizing the process of finding the critical value based on the level of significance and degrees of freedom. It explains how to use a calculator or table to find critical values for left-tailed, right-tailed, and two-tailed tests. The summary also covers how to determine the test statistic using a formula that includes the sample mean, population mean, sample standard deviation, and sample size. The TI-83/84 calculator's process for finding the standardized test statistic is outlined, along with examples of how to interpret the results for hypothesis testing.

10:02

🔍 Hypothesis Testing for Mean Prices

This section applies hypothesis testing to determine if there is enough evidence to reject a used-car dealer's claim about the mean price of a 2008 Honda CRV. It guides through writing the hypothesis statements, identifying the level of significance (alpha), finding the critical value, calculating the test statistic, and determining the rejection region. The example concludes with the interpretation of the test results in the context of the original claim.

15:04

🌐 Testing pH Level Claims with Hypothesis Testing

The paragraph demonstrates how to use hypothesis testing to evaluate an industrial company's claim about the pH level of water in a nearby river. It involves writing the hypothesis statements, identifying the significance level (alpha), determining the degrees of freedom, finding critical values for a two-tailed test, calculating the test statistic, and comparing it to the rejection region. The outcome is interpreted to decide whether there is enough evidence to reject the company's claim.

20:06

📊 Hypothesis Testing with Given Data

This section illustrates how to perform hypothesis testing using a list of data, such as lead concentrations in traditional medicines. It explains the process of identifying the hypothesis statements, finding the critical value at a 0.05 significance level, calculating the test statistic using the data list in a calculator, and comparing it to the critical value to determine if the null hypothesis should be rejected or not.

25:10

📈 Z-test for Proportions in Hypothesis Testing

The paragraph introduces the Z-test for proportions, a method used when the binomial distribution condition is met. It explains the formula for the standardized test statistic (Z value) and how to find the critical value (Z sub-alpha) using a calculator or table. The process includes identifying the hypothesis statement, determining the level of significance (alpha), and using the calculator to find the test statistic by comparing it to the critical value to decide whether to reject the null hypothesis.

30:11

📝 Hypothesis Testing for Research Claims

This section describes how to apply hypothesis testing to research claims, using examples of cell phone usage and internet access. It outlines the steps to write hypothesis statements, identify the level of significance (alpha), find critical values, calculate the test statistic, and interpret the results to support or reject the claim. The importance of using the correct wording in the decision statement based on the hypothesis test outcome is emphasized.

35:12

🔢 Calculation of Test Statistic in Hypothesis Testing

The paragraph focuses on the calculation of the test statistic in hypothesis testing, particularly for proportions. It explains how to use a calculator to find the test statistic (Z value) by entering the sample percentage, sample size, and population proportion. The process includes identifying the hypothesis statement, calculating the number of successes (x value), and comparing the test statistic to the critical value to make a decision about the claim.

40:14

📉 Decision Making in Hypothesis Testing

This section emphasizes the importance of proper decision making in hypothesis testing, with examples of claims about college graduates' views on the value of a college degree. It explains how to write hypothesis statements, determine the critical values for a two-tailed test, calculate the test statistic, and compare it to the critical values to decide whether to reject the null hypothesis. The summary highlights the correct interpretation of the test results in the context of the original claim.

45:16

📊 Hypothesis Testing Outcomes and Evidence

The final paragraph discusses the outcomes of hypothesis testing and the evidence required to reject or support a claim. It provides examples of hypothesis statements with claims on both the null and alternative hypotheses, explains how to find critical values, calculate test statistics, and interpret the results to make informed decisions. The summary underscores the need for accurate statement formulation and evidence evaluation in hypothesis testing.

Mindmap

Keywords

💡Hypothesis Testing

Hypothesis testing is a statistical method used to make decisions about a population parameter based on a sample. It's central to the video's theme as it provides the framework for evaluating claims or hypotheses about a population. For example, the script discusses different types of hypothesis tests, such as left-tail, right-tail, and two-tailed tests, and how they relate to the rejection region determined by the alternative hypothesis.

💡Null Hypothesis (H0)

The null hypothesis is a statement of no effect or no difference that is tested with a statistical significance test. It serves as the default assumption in hypothesis testing. In the script, the null hypothesis is often set up to be rejected in favor of the alternative hypothesis if the test statistic falls into the rejection region.

💡Alternative Hypothesis (H1 or Ha)

The alternative hypothesis is a statement that contradicts the null hypothesis and represents the research hypothesis that the researcher is testing. The script explains that the rejection region is always based on the alternative hypothesis, which can be less than, greater than, or not equal to the null hypothesis.

💡Critical Value

The critical value is the threshold value determined by the significance level (alpha) that separates the rejection and non-rejection regions of a statistical test. The script emphasizes the importance of identifying the critical value based on the type of hypothesis test being conducted and how it is used to determine if the null hypothesis is rejected.

💡Significance Level (Alpha)

The significance level, denoted as alpha, is the probability of rejecting the null hypothesis when it is true. It is a key concept in hypothesis testing, as it helps determine the critical value and the rejection region. The script provides examples of how alpha is used to find the critical value for different types of tests.

💡Test Statistic

A test statistic is a summary of the data that is used to make a decision in a statistical hypothesis test. The script explains that the test statistic, such as the t-statistic or z-statistic, is calculated using a specific formula and compared to the critical value to decide whether to reject the null hypothesis.

💡T-Test

The t-test is a statistical test used to determine if there is a significant difference between the means of two groups, especially when the population standard deviation is unknown. The script discusses the t-test for a mean and explains when and how it is used, including the conditions for its application and the formula for the standardized test statistic.

💡Degrees of Freedom

Degrees of freedom represent the number of independent values in a set that can vary without constraint. In the context of the script, the degrees of freedom are calculated as the sample size minus one and are crucial for determining the critical value from the t-distribution table or using a calculator.

💡Rejection Region

The rejection region is the range of values for which the null hypothesis is rejected. The script explains that the rejection region is determined by the critical value and the type of hypothesis test (left-tail, right-tail, or two-tailed), with the test statistic falling into this region leading to the rejection of the null hypothesis.

💡P-Value

The p-value is the probability that the test statistic would fall at least as extreme as the observed value, assuming the null hypothesis is true. Although not explicitly mentioned in the script, the concept of the p-value is implied when discussing test statistics and their comparison to critical values in hypothesis testing.

💡Z-Test

The z-test is a statistical test used to determine if there is a significant difference between the sample proportion and a known proportion. The script discusses the z-test for proportions, explaining the conditions under which it can be used and the formula for calculating the standardized test statistic.

Highlights

Review of hypothesis testing fundamentals including the nature of tests and types of hypotheses.

Explanation of the rejection region based on the alternative hypothesis for left-tail, right-tail, and two-tailed tests.

Critical value determination based on the level of significance (alpha).

Use of the t-test for a mean when the population standard deviation is unknown.

Conditions for using the t-test, including normal distribution or sample size greater than or equal to 30.

Formula for the standardized test statistic used in t-tests.

Finding critical values using a T-distribution table or calculator.

Procedure for identifying alpha, degree of freedom, and critical value in hypothesis testing.

Use of the TI-84 calculator for finding critical values and test statistics.

Interpretation of test results in the context of the original claim.

Example of hypothesis testing with a used-car dealer's claim about the mean price of a 2008 Honda CRV.

Process of hypothesis testing for proportions using the Z-test.

Conditions for using the Z-test for population proportions, including sample size and success/failure rates.

Formula for calculating the standardized test statistic Z in proportion testing.

Finding critical values for Z-tests using calculators or tables.

Example of testing a claim about the percentage of US adults with wireless internet access on laptops.

Importance of correct hypothesis statement formulation and decision-making based on test outcomes.

Transcripts

Browse More Related Video

Elementary Stats Lesson #18

One Tailed and Two Tailed Tests, Critical Values, & Significance Level - Inferential Statistics

Elementary Statistics Chapter 8 - Introduction Hypothesis Testing Part 1 Lesson 1

Math 119 Chap 8 part 1

8.3.1 Testing a Claim About a Mean - With Sigma Not Known, Three Equivalent Methods

t-Test - Full Course - Everything you need to know

Related Tags

Hypothesis Testing T-Test Z-Test Critical Value Statistical Analysis Sample Mean Population Proportion Data Interpretation Research Method Educational Content Mathematics Tutorial