Unit II: Lec 10 | MIT Calculus Revisited: Single Variable Calculus

MIT OpenCourseWare

5 May 201142:59

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script delves into the concept of the indefinite integral, or antiderivative, in calculus. It introduces the 'D-machine' analogy to explain how differentiation works and highlights the non-one-to-one nature of the derivative function. The script uses the Mean Value Theorem to establish that every function with a given derivative is of the form 'f(x) + c'. It also covers finding antiderivatives through examples and emphasizes the importance of understanding derivative properties to solve integral problems, concluding with a geometric interpretation of differentials.

Takeaways

📚 The lecture introduces the concept of the 'indefinite integral' or 'antiderivative', emphasizing the educational significance of focusing on a few concepts with broad applications rather than many concepts with limited uses.
🔄 The professor prefers the term 'inverse derivative' or 'inverse differentiation' to highlight the connection with inverse functions, which is a recurring theme in the course.
🤖 The 'D-machine' metaphor is used to explain the process of differentiation, where the input is a differentiable function and the output is its derivative, illustrating the non-one-to-one nature of the derivative function.
🔍 The Mean Value Theorem is discussed to show that every function with a given derivative can be expressed as a particular function plus a constant, which is crucial for understanding antiderivatives.
📉 The concept of 'D inverse' or the set of all functions whose derivative is a given function is introduced, explaining that finding one function in this set allows for the identification of the entire set by adding an arbitrary constant.
📈 The 'D inverse' notation is contrasted with the more traditional integral notation, showing that they are equivalent and both aim to find functions with a given derivative.
📝 The properties of derivatives, such as the derivative of a sum being the sum of derivatives and the derivative of a constant times a function being the constant times the derivative of the function, are highlighted as key to solving integral problems.
📚 The script provides examples and illustrations to demonstrate the process of finding antiderivatives, including the use of the chain rule and handling implicit differentiation problems.
🔢 The importance of method over the specific answer in calculus is emphasized, as the method can be applied to solve a variety of problems, not just the ones explicitly solved in the lecture.
📉 The use of differentials as an alternative to derivatives is discussed, showing that they provide an intuitive and algebraically simpler technique for solving certain types of problems, especially those with implicit relationships.
🌐 The lecture concludes by connecting the concepts discussed to real-world applications, where knowing the derivative (or slope) can help determine the original function (or curve), which is often necessary in physical sciences.

Q & A

What is the main topic discussed in the script?
-The main topic discussed in the script is the concept of the indefinite integral, also known as the antiderivative, in calculus.
What is the 'D-machine' as described in the script?
-The 'D-machine' is a conceptual tool used to represent the process of differentiation, where the input is a differentiable function and the output is its derivative.
Why is the derivative function 'D' not one-to-one according to the script?
-The derivative function 'D' is not one-to-one because different functions can have the same derivative. For example, 'x squared' and 'x squared plus 7' both have the derivative '2x'.
What does the Mean Value Theorem contribute to the understanding of derivatives and antiderivatives?
-The Mean Value Theorem helps establish that if two functions have the same derivative, they must differ by a constant, which is crucial for understanding the existence of antiderivatives.
What is the relationship between differentiation and the concept of equivalence with respect to a constant?
-With respect to differentiation, two functions that differ by a constant are considered equivalent because the derivative of a constant is zero, and thus the derivative does not change when a constant is added to a function.
What is the traditional notation used to represent the 'D inverse' of a function as mentioned in the script?
-The traditional notation used to represent the 'D inverse' of a function is the integral symbol, ∫, which signifies the antiderivative or the set of all functions whose derivative is the given function.
How does the script explain the process of finding the antiderivative of a function?
-The script explains that to find the antiderivative, one must find a function whose derivative matches the given function and then add an arbitrary constant to account for all possible antiderivatives in the family of functions.
What property of derivatives is used to justify the integral of a sum being equal to the sum of the integrals?
-The property of derivatives that the derivative of a sum is equal to the sum of the derivatives is used to justify this rule for integrals.
How does the script illustrate the use of differentials in solving problems involving derivatives?
-The script illustrates the use of differentials by showing how cross-multiplying differentials can simplify the process of finding functions whose derivatives have a given relationship, as in the example where 'dy/dx' equals '1/(y^2)'.
What is the geometric interpretation of the problem where 'dy/dx' is 'minus x' over 'y' and 'x' equals 3, 'y' equals 4?
-The geometric interpretation is that the curve described by this relationship is a circle centered at the origin with a radius of 5, as the derivative at any point is the negative of the x-coordinate over the y-coordinate.

Outlines

00:00

📚 Introduction to Inverse Derivatives

The speaker introduces the concept of the 'indefinite integral' or 'antiderivative', preferring the term 'inverse derivative' to emphasize its relationship with inverse functions. The 'D-machine' analogy is used to explain the process of differentiation, highlighting that the derivative is a rule assigning a new function to a given differentiable function. The non-uniqueness of the inverse derivative due to the constant difference in functions with the same derivative is discussed, and the mean value theorem is mentioned as a tool to address this issue.

05:02

🔍 Exploring the Inverse Derivative's Nature

This paragraph delves deeper into the properties of the 'D-machine', illustrating that it is not one-to-one due to different functions having the same derivative. The mean value theorem is used to assert that every function with a derivative of '2x' must be of the form 'x squared plus c'. The paragraph also introduces the notation 'e sub f' to denote functions that differ by a constant, emphasizing the importance of understanding the derivative to solve inverse derivative problems.

10:03

📈 Deriving the Inverse Derivative Notation

The speaker explains the process of finding the inverse derivative by starting with a known function and its derivative, using the example of 'h of x' and showing the steps to find its inverse. The concept of 'D inverse' is introduced as the set of all functions whose derivative is a given function. The importance of the method over the specific answer is highlighted, and the process of finding the inverse derivative is compared to unscrambling an egg.

15:05

📘 Examples and Techniques for Finding Antiderivatives

The paragraph provides a detailed example of finding the antiderivative of a function, using the product rule and chain rule for differentiation. It then explains how to find the family of functions that have a given derivative by adding an arbitrary constant to a particular function found to have that derivative. The paragraph also introduces common recipes for antiderivatives, such as the inverse derivative of 'x to the n'.

20:06

📖 The Role of the Chain Rule in Antiderivatives

This section discusses the importance of the chain rule in finding antiderivatives, especially when dealing with complex expressions. It uses the example of differentiating 'x squared plus 1' to the 8th power and explains the mistake of incorrectly applying the chain rule. The correct application of the chain rule is emphasized, and the paragraph concludes with a comparison of the complexity of different problems and the insights gained from understanding derivatives.

25:08

🔧 The Mechanics of Antiderivatives and Differentials

The speaker transitions from the conceptual understanding of antiderivatives to the practical computation, emphasizing the importance of practice. The paragraph introduces the concept of the 'script D-machine', which outputs differentials instead of derivatives, and shows that knowing the differential can lead to the same function as knowing the derivative. The use of differentials is illustrated with a problem involving 'dy/dx' equal to '1 over y squared', leading to the solution 'y equals the cube root of 3x plus c'.

30:08

📐 Geometric Interpretation of Differentials

The paragraph provides a geometric interpretation of the relationship between a curve and its derivative, using the example of a circle and its tangent lines. It explains how the slope of the tangent is the negative reciprocal of the radius's slope at any point on the circle. The geometric interpretation is linked back to the algebraic method of solving for functions using differentials, emphasizing the circle's unique property of having a derivative equal to the negative x-coordinate over the y-coordinate.

35:10

🎓 Conclusion and Motivation for Inverse Derivatives

In conclusion, the speaker summarizes the importance of understanding inverse derivatives, relating it to physical applications where the slope is given, and the curve must be determined. The motivation for learning this topic is to switch the emphasis from finding the slope given a curve to finding the curve given a slope. The speaker also mentions that more information will be available in the text and exercises, and thanks the Gabriella and Paul Rosenbaum Foundation for funding the video.

Mindmap

Keywords

💡Indefinite Integral

The indefinite integral, also known as the antiderivative, is a fundamental concept in calculus that represents the family of functions whose derivative is a given function. In the video, the professor introduces the concept as the inverse operation of differentiation, emphasizing its importance in understanding the relationship between a function and its derivative. The script uses the term to explain how to find all functions that, when differentiated, yield a specific function, such as finding the antiderivative of 'x^n'.

💡Derivative

The derivative is a concept in calculus that measures how a function changes as its input changes. It is the fundamental notion used to define the rate of change or slope of a function at any given point. In the video, the derivative is discussed in the context of a 'D-machine,' which takes a function as input and produces its derivative as output, illustrating the process of differentiation.

💡Antiderivative

An antiderivative is synonymous with the indefinite integral and represents the reverse process of differentiation. It is used to find the original function when given its derivative. The video script discusses finding antiderivatives as a way to understand the inverse relationship between a function and its derivative, using the mean value theorem to ensure the correctness of the antiderivative found.

💡Differentiation

Differentiation is the process of finding the derivative of a function, which describes the sensitivity of the output of a function to changes in its input. The video uses the concept of differentiation to explain how to determine the rate of change and introduces the 'D-machine' as a metaphorical device that performs this operation.

💡Mean Value Theorem

The Mean Value Theorem is a fundamental theorem in calculus that provides a connection between the derivative of a function and the average rate of change of the function over an interval. In the video, the theorem is used to justify why two functions with the same derivative must differ by a constant, which is crucial when finding antiderivatives.

💡Inverse Functions

Inverse functions are functions that 'reverse' the effect of the original function. In the context of the video, the professor discusses the concept of inverse functions in relation to antiderivatives, explaining how finding an antiderivative is akin to reversing the process of differentiation to return to the original function.

💡Constant of Integration

The constant of integration is an arbitrary constant, typically denoted by 'C', that is added to an antiderivative to account for the fact that when differentiating, the derivative of a constant is zero. The video script mentions this concept when explaining that the family of antiderivatives of a given function includes all functions that differ by a constant.

💡Differential

A differential represents an infinitesimally small change in a function, often denoted as 'dx' for the input and 'dy' for the output. In the video, the script contrasts the 'D-machine', which outputs derivatives, with a 'script D-machine', which outputs differentials, providing an alternative perspective on the relationship between a function and its rate of change.

💡Chain Rule

The chain rule is a fundamental theorem in calculus for differentiating composite functions. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. The video script refers to the chain rule when discussing how to differentiate more complex functions, such as those involving products or quotients.

💡Product Rule

The product rule is a derivative rule that applies to the product of two functions. It states that the derivative of the product is the derivative of the first function times the second function plus the first function times the derivative of the second function. The video script uses the product rule in the example where the professor differentiates a function that is a product of two terms.

💡Quotient Rule

The quotient rule is a derivative rule for differentiating a quotient of two functions. It states that the derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. The video script briefly touches on the quotient rule when discussing the differentiation of a function that is a quotient.

Highlights

Introduction to the concept of the 'indefinite integral' or 'antiderivative' in calculus.

The 'D-machine' analogy for understanding the process of differentiation.

Discussion on the non-one-to-one nature of the derivative function, highlighting that different functions can share the same derivative.

Explanation of the Mean Value Theorem's role in establishing the relationship between a function and its derivative.

The importance of constants in antiderivatives and how they affect the family of functions with a given derivative.

Differentiation of a product and the application of the chain rule.

The method of finding antiderivatives by starting with the answer and working backward to the problem.

Generalization of the process to find the 'D inverse' of a function.

The concept of 'e sub f' notation to represent functions that differ by a constant.

Illustration of finding antiderivatives using specific examples and the importance of the method over the result.

The property of derivatives that allows for the differentiation of a constant times a function to be separated.

Mistakes to avoid when finding antiderivatives and the correct application of the chain rule.

The use of implicit differentiation and its connection to the inverse derivative.

Solving for functions given their derivatives using algebraic manipulation and the properties of derivatives.

The transition from 'D inverse' notation to the more traditional integral notation used in calculus.

Basic integral formulas and properties, such as the integral of a sum and a constant times a function.

The geometric interpretation of derivatives and how they relate to the physical world, with an example of a circle's derivative.

The use of differentials as an alternative method to solve problems involving derivatives, providing an intuitive approach.

Final thoughts on the importance of understanding both differentiation and antidifferentiation for practical applications.

Transcripts

Browse More Related Video

Calculus - Lesson 16 | Indefinite and Definite Integrals | Don't Memorise

Proof of fundamental theorem of calculus | AP Calculus AB | Khan Academy

Solving for the constant in the general anti-derivative

AP Calculus AB Crash Course Day 4 - Differentiation and the Mean Value Theorem

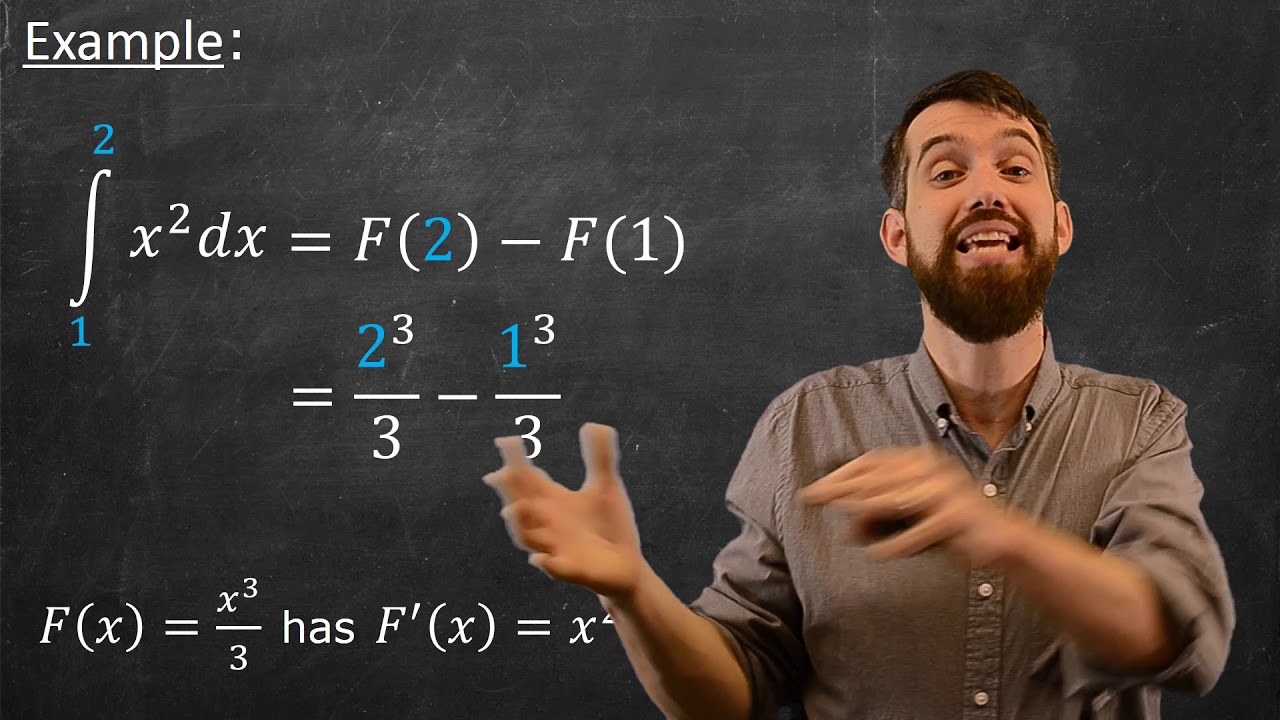
Fundamental Theorem of Calculus II

Initial Value Problems!

Related Tags

Calculus Antiderivatives MIT Differentiation Integrals Educational Mathematics Differentials Inverse Functions Educational Resources