Calculus Chapter 4 Lecture 34 Volume & Dimension
TLDRIn this calculus lecture, Professor Greist explores the concept of volume in various dimensions, starting from the familiar 3D shapes to the abstract nth dimension. He introduces the idea of hypervolume and discusses the properties of n-dimensional cubes, simplices, and balls. The lecture delves into the volumes and surface areas of these shapes, highlighting the diminishing volume of n-dimensional balls as dimensions increase. It concludes by emphasizing the intellectual achievement of measuring these higher-dimensional objects through rational thought and calculus.
Takeaways
- 📚 The lecture introduces the concept of volume and dimension in calculus, exploring beyond the familiar three dimensions to the nth dimension.
- 📏 The first dimension is the real number line, which can be represented by a single variable x, and is essentially length.
- 📐 The second dimension is the coordinate plane with two variables, x and y, representing area.
- 📊 In the third dimension, we have volume, which is calculated by multiplying length, width, and height, and is represented by variables x, y, and z.
- 🔍 The fourth dimension and beyond are challenging to visualize but can be conceptualized by adding more coordinates, such as x1, x2, x3, x4, etc.
- 📈 The concept of 'hypervolume' or n-dimensional volume is introduced as a generalization of volume, area, and length to higher dimensions.
- 🔢 Zero-dimensional volume is the count of points, which is essentially a point itself.
- 🔮 The unit n-dimensional cube is defined by points in n-dimensional space with coordinates satisfying 0 ≤ x_i ≤ 1 for all i.
- 📉 The volume of an n-dimensional simplex is given by 1/n!, which is derived using calculus and integration.
- 🌐 The unit ball in n-dimensions is defined by points where the sum of the squares of the coordinates is less than or equal to 1, and its volume decreases as the dimension increases.
- 📉 The volume of an n-dimensional ball of radius 1 is given by complex formulas involving pi and factorials, and it tends to zero as the dimension increases.
- 🏺 In higher dimensions, the volume of a unit cube can be larger than that of a unit ball, contrary to the case in lower dimensions where the ball has more volume.
Q & A
What is the main topic of Professor Greist's lecture 34?
-The main topic of the lecture is the concept of volume and dimension in various dimensions, starting from the first dimension up to the nth dimension.
What does the term 'fourth dimension' commonly refer to in the context of this lecture?
-In the context of this lecture, the 'fourth dimension' refers to an additional spatial dimension beyond the three dimensions of length, width, and height, and is part of a broader exploration of the nth dimension.
How does the lecture define the progression from one dimension to the next?
-The lecture defines the progression by adding another coordinate for each new dimension. For example, the first dimension is a real number line with coordinate X, the second dimension adds a second coordinate Y, and so on, with subscripts used for higher dimensions (e.g., X1, X2, X3, X4).
What is the definition of 'volume' in the context of higher dimensions as discussed in the lecture?
-In the context of higher dimensions, 'volume' is defined as 'hypervolume' for n-dimensional spaces. It is an extension of the concept of volume from three dimensions to spaces with more dimensions.
What is the relationship between the number of dimensions and the concept of 'volume'?
-As the number of dimensions increases, the concept of 'volume' transitions from length in one dimension, to area in two dimensions, to the familiar volume in three dimensions, and to hypervolume in higher dimensions.
What are the three shapes used in the lecture to build intuition for n-dimensional volume?
-The three shapes used are cubes, simplices (analogs of triangles or pyramids), and balls (spheres).
How is the unit n-dimensional cube defined in the lecture?
-The unit n-dimensional cube is defined as the set of points in n-dimensional space where the coordinates X sub I satisfy the inequalities X sub I greater than or equal to zero and less than or equal to one for all I.
What is the significance of the diagonal of an n-dimensional cube?
-The diagonal of an n-dimensional cube, which connects opposite corners, has a length that can be shown to be the square root of n, indicating that even small unit cubes can have corners very far apart in high dimensions.
How does the lecture describe the volume of an n-dimensional simplex?
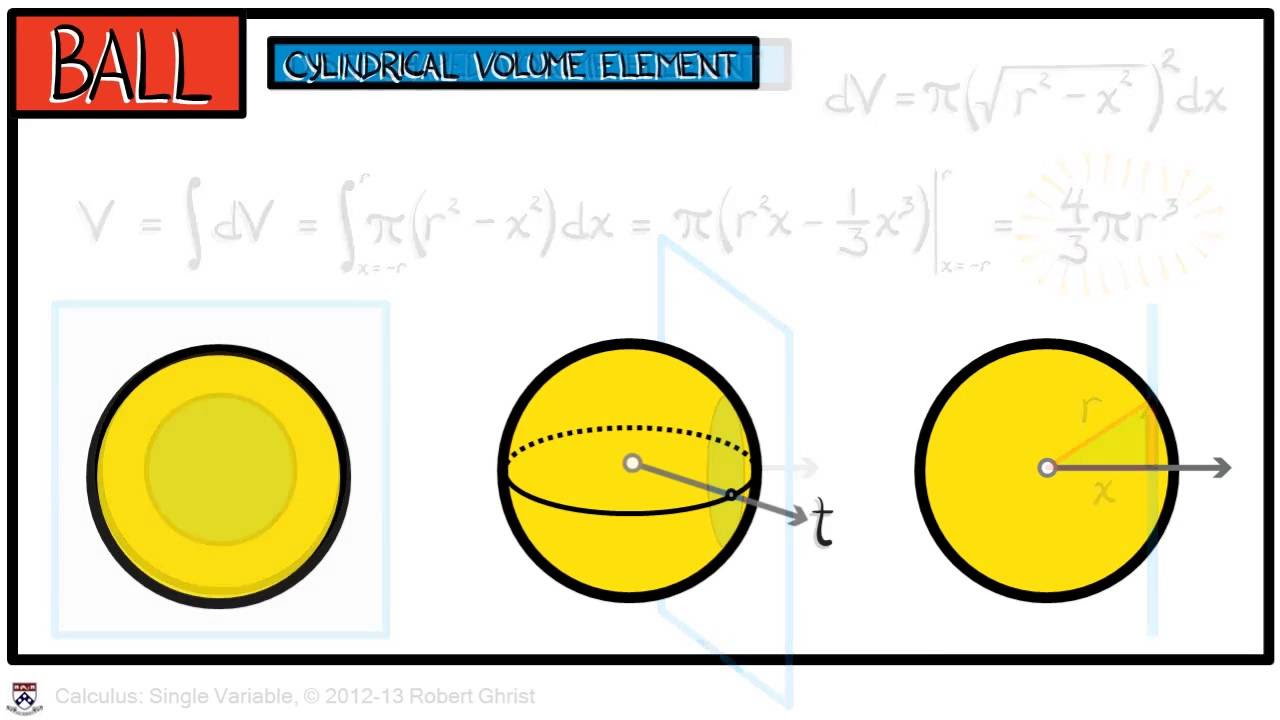
-The volume of an n-dimensional simplex is described as being proportional to 1 over n factorial (1/n!), which is derived from the pattern observed in lower dimensions and confirmed through calculus.
What observation is made about the volume of an n-dimensional ball as the dimension increases?
-As the dimension increases, the volume of an n-dimensional ball of radius 1 goes to zero rapidly due to the factorial in the denominator outpacing the power of the radius.
What conclusion is drawn from the comparison between the volume of a unit ball and a unit cube in higher dimensions?
-In higher dimensions, the volume within a unit cube can exceed that of a concentric unit ball because the corners of the cube extend further out than the ball, indicating that cubes can 'beat' balls in terms of volume in higher dimensions.
Outlines
📚 Introduction to Higher Dimensions and Volumes
Professor Greist begins lecture 34 by introducing the concept of volume in various dimensions, starting from the familiar two and three-dimensional shapes to the abstract notion of higher dimensions. He poses the question of what constitutes the fourth dimension and extends this to the nth dimension. The lecture aims to explore the idea of volume in these higher dimensions, starting with the fundamental concept of a point in zero dimension and moving up to the hypervolume in n-dimensions. The professor uses the analogy of a sound system's slider bars to help visualize n-dimensional cubes, where each slider represents a coordinate in the n-dimensional space.
📐 Understanding N-Dimensional Volumes and Shapes
The second paragraph delves deeper into the concept of n-dimensional volumes, specifically focusing on the unit n-dimensional cube and its properties. The professor explains how the volume of these cubes can be understood by considering the product of their side lengths, which is always 1. He also discusses the surface area of these cubes, which is 2^n, and the diagonal length, which is the square root of n. The paragraph introduces two additional shapes for consideration: simplices, which are the higher-dimensional analogs of triangles and pyramids, and balls, which are the spherical equivalents in higher dimensions.
📏 Calculating Volumes of N-Dimensional Simplices and Balls
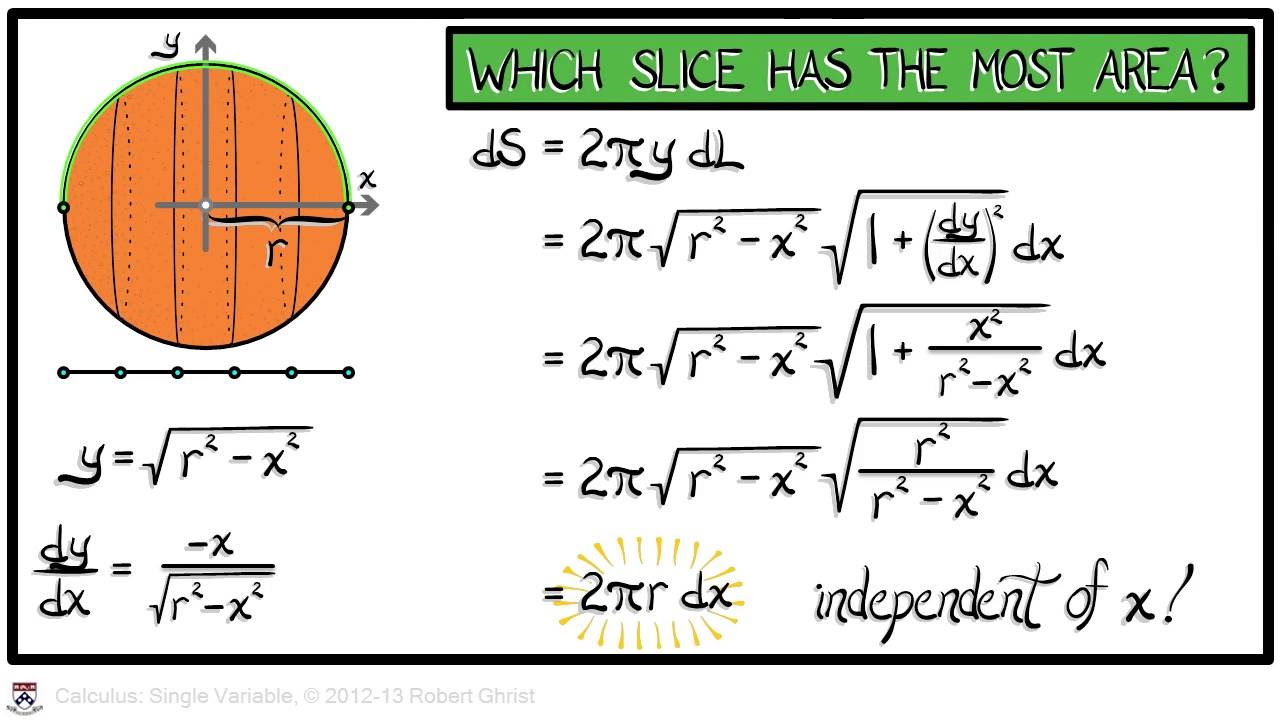
In the third paragraph, the professor discusses the calculation of volumes for n-dimensional simplices and balls. For simplices, he explains that the volume can be determined by slicing the shape and integrating the resulting volume elements, leading to the formula for the volume of an n-dimensional simplex being 1/n!. The discussion then moves to n-dimensional balls, explaining their definition and the pattern observed in their volumes, which is related to the radius raised to the nth power. The professor also touches on the concept of surface area for these shapes and how it changes with the dimension.
🌐 The Implications of Increasing Dimensionality on Volume
The final paragraph explores the implications of increasing dimensionality on the volume of unit balls and cubes. The professor points out that contrary to intuition, the volume of a unit ball decreases as the dimension increases, approaching zero rapidly due to the factorial in the denominator outweighing the power of the radius. This leads to a discussion on the relationship between the volumes of balls and cubes in various dimensions, highlighting that in higher dimensions, the corners of a cube can contain more volume than the corresponding ball. The lecture concludes by emphasizing the abstract nature of these concepts and the intellectual achievement of measuring objects that cannot be experienced through the senses.
Mindmap
Keywords
💡Calculus
💡Dimension
💡Volume
💡N-dimensional Cube
💡Coordinate System
💡Hypervolume
💡Simplex
💡Integration
💡Unit Ball
💡Factorial
💡Pythagorean Theorem
Highlights
Introduction to the concept of dimensions beyond the third, exploring the fourth dimension and higher (nth dimension).
Explanation of the progression from one-dimensional real number line to multi-dimensional spaces with coordinates X1, X2, ..., Xn.
Discussion on the difficulty of visualizing higher dimensions and the use of subscripts for coordinate variables.
Introduction of three simple shapes for understanding n-dimensional volume: cubes, simplices, and balls.
Definition of zero-dimensional volume as counting the number of points.
Generalization of volume concepts from length, area, and volume to n-dimensional hypervolume.
Description of the n-dimensional cube and its properties, including unit length sides and the concept of hypervolume.
Exploration of the surface area of n-dimensional cubes and its relationship to the number of boundary phases.
Calculation of the diagonal length of an n-dimensional cube using the Pythagorean theorem.
Counting the number of corners in an n-dimensional cube and the pattern observed as dimension increases.
Introduction to the n-dimensional simplex, its definition, and properties compared to a cube.
Derivation of the volume of n-dimensional simplices using calculus and integration.
Explanation of the n-dimensional ball, its definition, and the constraints of its coordinates.
Pattern recognition in the volume calculation of n-dimensional balls and its relation to the radius.
Observation that the volume of a unit ball decreases rapidly as the dimension increases, approaching zero.
Comparison between the volumes of n-dimensional balls and cubes, and the surprising result in higher dimensions.
Reflection on the significance of measuring objects in higher dimensions that cannot be experienced by human senses.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: