Calculus Chapter 4 Lecture 32 Volumes

Penn Online Learning

23 Jun 201615:55

EducationalLearning

32 Likes 10 Comments

TLDRIn this calculus lecture, Professor Greist explains how to compute volumes in 3D, starting with simple shapes like rectangular prisms, cylinders, and balls, and progressing to cones. He discusses the integral formulas used to determine volumes, emphasizing the importance of finding the correct volume element. The lecture includes detailed examples and multiple methods for computing volumes, such as slicing, using cylindrical and spherical elements, and integrating volume elements. It concludes with insights into the classical volume formulas, revealing why certain constants appear in these formulas and preparing students for more complex objects in future lessons.

Takeaways

📐 Understanding volumes in 3D involves extending the methods used for computing areas in 2D.
🟦 The volume of a rectangular prism can be computed by integrating along one of its principal directions.
🛢️ The volume of a cylinder can be found using different methods such as slicing laterally, using an angular wedge, or an annular area element.
⚽ The volume of a sphere can be computed by slicing it into discs or using cylindrical or spherical shells.
📏 The integration of volume elements varies in complexity depending on the shape being considered.
🔺 The volume of a cone with a circular base is obtained by integrating the area of its disc slices.
📐 For cones with other base shapes, the volume formula still follows a similar pattern involving integration of scaled slices.
🧮 The general formula for the volume of a cone is one-third the base area times the height, regardless of the base shape.
📊 The key to simplifying volume integrals lies in identifying the correct volume element.
🔍 Classical volume formulas like those for cones and spheres reveal deeper mathematical insights upon closer examination.

Q & A

What is the main topic of Lecture 32 in Professor Greist's calculus class?
-The main topic of Lecture 32 is computing simple volumes in 3D, progressing from computing areas in 2D.
What classical shapes' volume formulae are discussed in the lecture?
-The lecture discusses the volume formulae of round balls, cones, and pyramids.
What is the fundamental formula for computing volume mentioned in the lecture?
-The fundamental formula for computing volume is the integral of the volume element.
How is the volume of a rectangular prism calculated?
-The volume of a rectangular prism is calculated by integrating one of the volume elements (W * H dx, L * H dy, or L * W dz) over the appropriate range, all resulting in length * width * height.
What are the three methods mentioned for computing the volume of a cylinder?
-The three methods are: using a lateral slice of thickness dx, using an angular wedge with dθ, and using an annular area element with dt.
How is the volume of a round ball computed using a lateral plane slice?
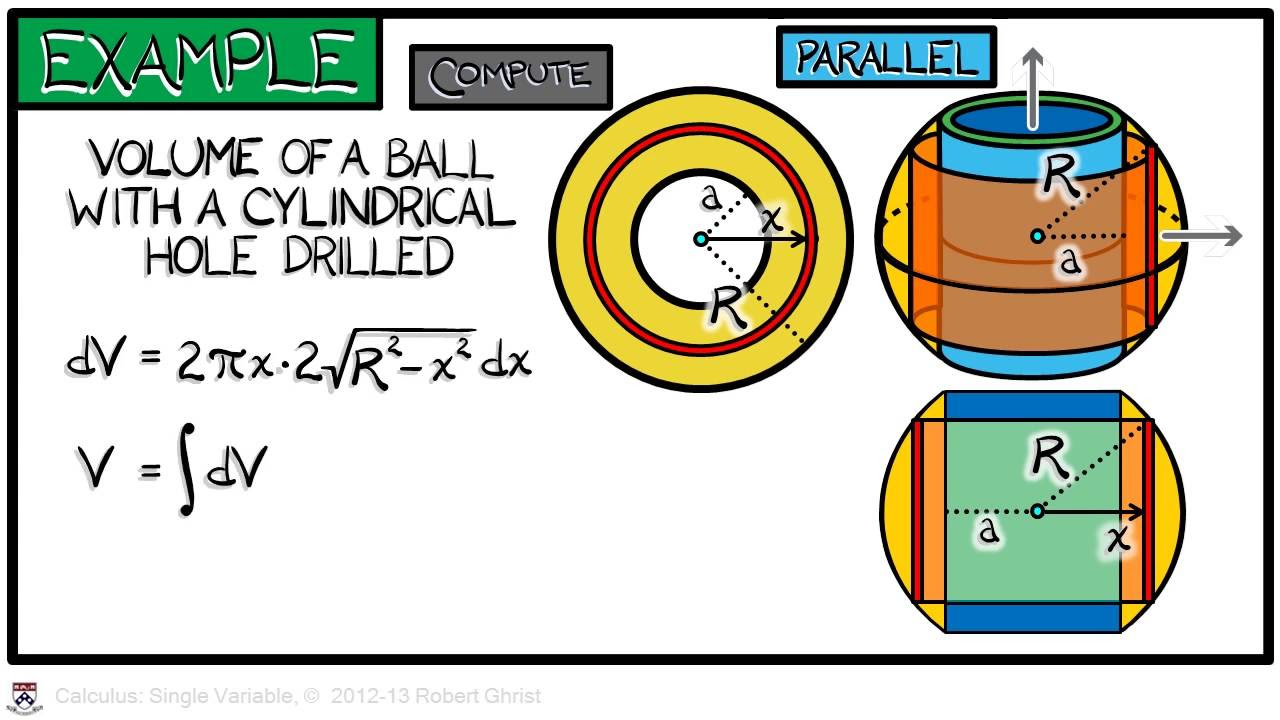
-The volume is computed by integrating the volume element π(R^2 - x^2) dx as x goes from -R to R, resulting in the familiar formula 4/3 πR^3.
What is the volume element when using cylindrical shells to compute the volume of a round ball?
-The volume element is 4πT√(R^2 - T^2) dt, which is then integrated as T goes from 0 to R.
How is the volume of a cone with a circular base calculated?
-The volume is calculated by integrating the volume element π(R/H * y)^2 dy as y goes from 0 to H, resulting in the formula 1/3 πR^2 H.
What is the general volume formula for any cone regardless of the shape of its base?
-The general volume formula for any cone is 1/3 the area of the base (B) times the height (H).
What is the insight provided in the lecture about the 1/3 factor in the volume formula for cones?
-The 1/3 factor comes from integrating y^2, reflecting the scaling of the area of the slices as you move up the height of the cone.

Outlines

00:00

📐 Introduction to Calculus and Simple Volumes

In this lesson, Professor Greist introduces the concept of calculating volumes in 3D, transitioning from 2D area calculations. He discusses classical shapes like rectangular prisms, cylinders, and balls, explaining how to derive their volume formulas. The focus is on finding the correct volume element, starting with simple shapes and progressing to more complex ones like cylinders and balls. Various methods, including slicing and integrating, are used to determine volumes, emphasizing the importance of understanding the volume element.

05:01

⚖️ Deriving the Volume of a Sphere

This paragraph explores different methods to derive the volume of a sphere. It begins with the traditional integral of a disc-shaped volume element, showing the calculation of the formula 4/3 PI R³. Alternative approaches, such as using cylindrical shells and spherical volume elements, are also discussed. The explanation includes setting up and solving the relevant integrals, demonstrating the versatility in methods and the importance of choosing an appropriate volume element for simpler calculations.

10:04

🔺 Calculating the Volume of Cones

Professor Greist discusses calculating the volume of a cone with a circular base, starting by positioning the cone upside down with the apex at the origin. By slicing the cone into parallel disks, the volume element is expressed as pi times x squared dy, integrating over the height. The explanation extends to cones with other base shapes, such as squares, generalizing the formula as one-third the area of the base times the height. This method highlights the uniformity in calculating volumes for various cone shapes by focusing on the area scaling factor.

15:05

🔍 Insights into Volume Formulas

The final paragraph delves into the reasons behind the 1/3 factor in the volume formula of a cone and the 4/3 PI factor for a sphere. The discussion ties back to integrating Y squared and reveals deeper mathematical insights into these classical formulas. The paragraph concludes by hinting at more complex objects to be covered in the next lesson, suggesting a transition from basic shapes to more advanced topics in volume calculations.

Mindmap

Keywords

💡Calculus

Calculus is a branch of mathematics that deals with rates of change and accumulation. In the context of this video, it is used to compute volumes of various 3D shapes through integration, which is a fundamental concept in calculus. The script discusses how calculus is applied to progress from 2D area computation to 3D volume computation.

💡Volume Element

A volume element is a small portion of a 3D shape that is used in integration to find the total volume. The script emphasizes that the key to computing volumes is identifying the correct volume element for the shape in question, which varies depending on how the shape is sliced or decomposed.

💡Rectangular Prism

A rectangular prism is a three-dimensional shape with six rectangular faces. The script uses it as an example of a simple shape where the volume element can be easily defined as the product of its width, height, and a differential slice length, integrated over the length of the prism.

💡Cylinder

A cylinder is a geometric shape with parallel circular bases connected by a curved surface. The video script explains different methods to compute the volume of a cylinder, such as using a lateral slice or an angular wedge, each yielding the formula πR^2H, where R is the radius and H is the height.

💡Sphere

A sphere is a perfectly symmetrical 3D shape where all points on the surface are equidistant from the center. The script discusses how to compute the volume of a sphere using various methods, including slicing it into discs or cylindrical shells, leading to the volume formula 4/3πR^3.

💡Integration

Integration is a mathematical process used to calculate the accumulated value of a function over an interval. In the script, integration is used to sum up the infinitesimally small volume elements to find the total volume of different shapes, such as cylinders, spheres, and cones.

💡Cone

A cone is a geometric shape with a circular base and a single vertex. The script explains how to compute the volume of a cone by slicing it with discs parallel to the base and integrating the resulting volume elements, leading to the volume formula 1/3πR^2H.

💡Volume Formula

A volume formula is an equation used to calculate the volume of a geometric shape. The script provides volume formulas for several shapes, such as the rectangular prism (LWH), cylinder (πR^2H), sphere (4/3πR^3), and cone (1/3πR^2H), and explains how these are derived through integration.

💡Spherical Shell

A spherical shell is a volume element used in the script to describe a thin layer of a sphere. The script mentions this concept when discussing an alternate method for calculating the volume of a sphere, where the volume element is considered as the surface area of the shell multiplied by its thickness.

💡Right Triangle

A right triangle is a triangle with one angle measuring 90 degrees. The script uses right triangles to determine the relationship between the radius of the disc in a sphere's cross-section and the distance from the center, which is essential for setting up the integral to find the sphere's volume.

💡Pi (π)

Pi, represented by the symbol π, is a mathematical constant that represents the ratio of a circle's circumference to its diameter. In the script, π is used in the volume formulas for shapes like cylinders and spheres, where the area of a circle (πR^2) is a component of the volume calculation.

Highlights

Introduction to Calculus lecture 32 on simple volumes, transitioning from 2D areas to 3D volumes.

Explaining the fundamental volume formula as the integral of the volume element.

Simplest example of calculating volume for a rectangular prism using different integrals.

Volume computation for a cylinder using different methods and volume elements.

Using lateral slices, angular wedges, and annular area elements to find cylinder volume.

Moving to more complex shapes, like a round ball, and the process of finding its volume element.

Deriving the volume of a sphere using the formula 4/3 PI R cubed.

Alternative method for finding the volume of a sphere using cylindrical shells.

Using spherical volume elements to compute the volume of a ball.

Highlighting the importance of choosing the proper volume element for simplifying integration.

Exploring the volume of a cone with a circular base and its derivation.

General formula for the volume of any cone, relating base area, height, and the scaling factor.

Insight into the classical volume formula of cones and the significance of the 1/3 factor.

Comparing the volume computation of cones with circular and square bases.

Understanding the pattern in volume computation for different base shapes of cones.

Upcoming lesson预告 on more complex objects and volume computation.

Transcripts

Browse More Related Video

Three-Dimensional Shapes Part 2: Calculating Volume

Calculus Chapter 4 Lecture 33 Complex Volumes

Calculus Chapter 4 Lecture 34 Volume & Dimension

Math Antics - Volume

Unit IV: Lec 3 | MIT Calculus Revisited: Single Variable Calculus

Topic 43-Volumes of Solids with Known Cross Sections