Why is the determinant like that?
TLDRThis video script explores the intriguing concept of determinants, starting from the basics of area in two dimensions with vectors to the more complex calculations in higher dimensions. It explains how the area function follows certain rules, such as scaling by constants and vector addition, leading to the determinant formula for 2x2 matrices. The script then extends these principles to 3D and n-dimensional spaces, illustrating the connection between determinants, volume, and orientation. The Leibniz formula for the n-dimensional determinant is introduced, highlighting the role of permutations and their signs in calculating the determinant.
Takeaways
- 🧩 The determinant is a fundamental concept in linear algebra that is deeply connected to the idea of area and volume in geometric spaces.
- 📐 In a two-dimensional space, the determinant can be visualized as the area of a parallelogram formed by two vectors, with the area function A obeying certain rules related to scaling and vector addition.
- 📏 The area of a unit square spanned by the basis vectors i-hat and j-hat is equal to one, which is a foundational rule for the area function.
- 🔄 If two vectors are collinear, the area of the parallelogram they form is zero, highlighting an important property of the area function.
- 🔢 The area function A is linear, meaning that it can pull constant factors out when vectors are scaled, and it behaves additively when vectors are added together.
- ↔️ The determinant captures the orientation of the parallelogram or higher-dimensional volumes, with a sign change occurring when the order of vectors is reversed.
- 🔄 The concept of orientation is intrinsic to the space, with the determinant indicating whether the motion from one vector to another is counterclockwise (positive area) or clockwise (negative area).
- 📉 The determinant of a 2x2 matrix can be derived by applying the area function rules to the coordinates of the vectors using the basis vectors i-hat and j-hat.
- 📊 Extending the concept to three dimensions, the determinant can represent the volume of a parallelepiped, with similar rules for scaling, addition, and orientation.
- 🔢 The determinant of a 3x3 matrix is calculated by considering the volume function V and applying the rules for scaling, addition, and permutation of vectors, resulting in a formula that includes both positive and negative terms based on orientation.
- 🔍 The generalization to n-dimensional space involves permutations of basis vectors and the concept of the sign of a permutation, which is crucial for understanding the determinant's role in capturing orientation in higher dimensions.
Q & A
What is the determinant and why is it significant in mathematics?
-The determinant is a scalar value that can be computed from a square matrix and is used to find the area or volume of geometric shapes in a space. It is significant because it is connected to various mathematical concepts, including area, volume, and orientation, and it helps in understanding the properties of linear transformations.
How does the concept of area lead to the formula for the determinant?
-The concept of area is used to define a function that measures the area of a parallelogram formed by two vectors. By considering the properties that this area function should satisfy, such as scaling with vector magnitude and orientation, we can derive the formula for the determinant.
What are the basis vectors i-hat and j-hat, and how are they related to the unit square?
-The basis vectors i-hat and j-hat represent the directions along the x-axis and y-axis, respectively, in a two-dimensional Cartesian coordinate system. They span the unit square, which has an area of one, and can be represented as column vectors or as part of a matrix.
What are the rules that the area function should obey according to the script?
-The area function should obey several rules: 1) The area of the unit square should be equal to one. 2) If two vectors lie on a straight line, the area should be zero. 3) The area should scale linearly with the magnitude of the vectors. 4) The area should be additive when vectors are combined. 5) Swapping the order of vectors should introduce a sign change, reflecting the orientation of the parallelogram.
How does stretching a vector affect the area of the parallelogram it forms with another vector?
-When a vector is stretched by a factor, the area of the parallelogram it forms with another vector is scaled by the same factor. For example, stretching a vector by a factor of 3 triples the area of the parallelogram.
What is the significance of the rule that states the area of a parallelogram formed by two vectors lying on a straight line is zero?
-This rule is significant because it implies that the orientation and position of vectors affect the area calculation. It also leads to the understanding that the area function is sensitive to the relative alignment of the vectors.
How does the concept of orientation relate to the determinant?
-The determinant captures the orientation of the space by introducing a sign change when the order of vectors is swapped. This sign change indicates whether the motion from one vector to another is counterclockwise (positive area) or clockwise (negative area).
What is the Leibniz formula for the determinant of an n-by-n matrix?
-The Leibniz formula for the determinant of an n-by-n matrix is a sum of n! many terms, each term corresponding to a permutation of the matrix's columns or rows, multiplied by the product of the chosen elements and the sign of the permutation.
How does the concept of a permutation relate to the calculation of the determinant?
-In the calculation of the determinant, each term corresponds to a permutation of the matrix's columns or rows. The sign of each term is determined by the number of swaps needed to arrange the permutation into the standard order, which is an even or odd number, resulting in a plus or minus sign.
What is a cofactor expansion, and how is it used in calculating the determinant?
-A cofactor expansion is a method of calculating the determinant by expanding it along a row or column, resulting in a sum of products of elements and their corresponding cofactors. The cofactors are determined by the sign of the permutation and the product of the remaining elements after removing a row and a column.
How does the script explain the transition from calculating the area of a parallelogram to finding the volume of a parallelepiped?
-The script explains that the transition from two-dimensional area calculation to three-dimensional volume calculation involves similar principles. The rules for volume are analogous to those for area, with the unit cube's volume being one, scaling with vector magnitude, and introducing a sign change for swapped vectors to capture orientation in 3D space.
Outlines
📐 Introduction to Determinants and Area
This paragraph introduces the concept of the determinant, explaining its connection to the area of a parallelogram formed by two vectors v and w in a two-dimensional space. The determinant is revealed not as a mere formula, but as a fundamental mathematical concept linked to the properties of area. The discussion begins with the area function A, which measures the area of the parallelogram as vectors are moved around, and establishes rules that this function must obey, such as the area of the unit square being equal to one. The paragraph also explores the effects of stretching or squishing vectors on the area and how the area behaves when vectors are added together, leading to the realization that the area function can introduce a negative sign, indicating the orientation of the parallelogram.
🌀 Understanding Vector Operations and Orientation
The second paragraph delves deeper into the implications of the rules governing the area function, particularly the introduction of orientation in space. It discusses how the simple properties of area can imply a natural concept of orientation, or handedness, in space. The paragraph then transitions to the calculation of the area of a parallelogram using the coordinates of vectors v and w, applying the established rules to derive the formula for the determinant of a 2-by-2 matrix. The discussion extends to three dimensions, examining the volume of a parallelepiped and the rules that govern it, such as the volume being zero when any two vectors are collinear and the effect of scaling vectors on volume. The orientation of 3D space is also explored, with the right-hand rule being introduced to determine the sign of the volume based on the order of vectors.
🔍 Exploring Permutations and the Sign of Determinants
This paragraph focuses on the concept of permutations and their significance in determining the sign of the determinant. It explains how the arrangement of vectors into the i-j-k order affects the volume calculation and introduces the braid diagram as a method to visualize and count the number of swaps needed to achieve this order. The sign of a permutation is defined as the remainder when the number of swaps is divided by two, which is also related to the number of crossings in the braid diagram. The paragraph establishes that the sign of a permutation is well-defined due to the rules governing braid diagrams, which prevent ambiguous crossings and ensure a consistent count of swaps.
📚 Generalizing Determinants to n-Dimensional Space
The final paragraph generalizes the concept of determinants to n-dimensional space, adapting the previously discussed rules to this higher-dimensional context. It explains how the n-dimensional volume can be calculated using the basis vectors e1 through en and how the determinant formula can be extended to n dimensions, resulting in the Leibniz formula. The paragraph also discusses the practical application of this formula, demonstrating how it works with a 4x4 matrix and explaining the process of cofactor expansion along the first column. The alternating pattern of pluses and minuses is highlighted as a correcting factor for the sign of permutations when rows and columns are struck out.
Mindmap
Keywords
💡Determinant
💡Parallelogram
💡Basis Vectors
💡Area Function
💡Scaling Vectors
💡Vector Addition
💡Orientation
💡Permutation
💡Leibniz Formula
💡Braid Diagram
💡n-Dimensional Space
Highlights
The determinant is connected to intriguing and beautiful mathematics, with a natural connection to the concept of area.
The area function A for a parallelogram formed by two vectors v and w changes as the vector tips are shifted around.
The area of the unit square spanned by basis vectors i-hat and j-hat should be equal to one, a fundamental rule for the area function.
If two vectors lie on a straight line, the parallelogram's area becomes zero, an important rule for the area function.
Scaling a vector by a factor affects the area proportionally, allowing constant factors to be pulled out of the area function A.
The area function A obeys the rule that adding vectors together results in the sum of the original areas.
Setting one vector to the negative of another reveals a relationship between the area of the parallelogram and vector orientation.
The sign of the area function introduces a concept of orientation, indicating left- or right-handedness in space.
The formula for the determinant of a 2-by-2 matrix is discovered through the application of area rules and coordinate representation.
In 3D, the volume of a parallelepiped follows similar rules to the area in 2D, including the effect of scaling vectors on volume.
Swapping vectors in the volume function introduces a minus sign, capturing the 3D space orientation.
The volume of a general parallelepiped is calculated using an expanded formula that accounts for vector coordinates and constant factors.
The determinant's Leibniz formula for an n-by-n matrix is introduced, summing over permutations of the basis vectors with their respective signs.
The sign of a permutation is defined by the number of swaps needed to arrange it into the natural order, modulo 2.
Braid diagrams provide a visual method to determine the sign of a permutation by counting the number of crossings.
The cofactor expansion along the first column of a matrix is explained, demonstrating how to apply alternating signs to permutations.
The process of calculating the n-dimensional determinant is outlined, emphasizing the role of permutations and their signs.
The video concludes with a practical demonstration of how the Leibniz formula works for a 4x4 matrix, showing the grouping of terms.
Transcripts
Browse More Related Video

n x n determinant | Matrix transformations | Linear Algebra | Khan Academy

The determinant | Chapter 6, Essence of linear algebra

PreCalculus - Matrices & Matrix Applications (21 of 33) Using the Determinant to Find the Inverse

Ch. 9.5 The Cross Product
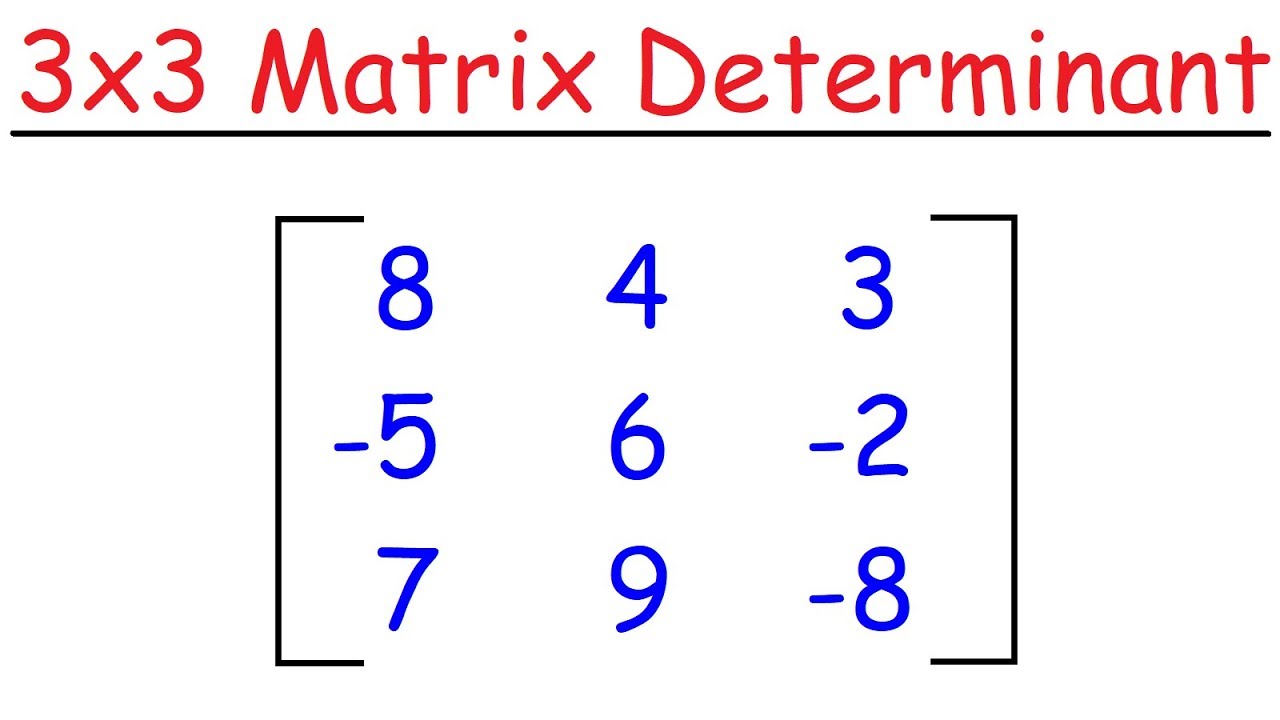
How To Find The Determinant of a 3x3 Matrix

Evaluating the Determinant of a Matrix
5.0 / 5 (0 votes)
Thanks for rating: