Unit IV: Lec 3 | MIT Calculus Revisited: Single Variable Calculus
TLDRThis lecture delves into the relationship between integral and differential calculus through the application of finding volumes of 3-dimensional shapes. The professor introduces '3-dimensional area' to draw parallels with area calculations, using cylinders as the basic building block. The discussion includes deriving the volume of a cone and exploring solid regions, emphasizing the importance of mathematical structure in understanding calculus. The lecture also covers methods for calculating volumes of solids of revolution, such as the method of cylindrical shells, providing a comprehensive look at the calculus behind volume calculations.
Takeaways
- 📚 The lecture introduces the concept of '3-dimensional Area', emphasizing the study of volumes in an analogous way to areas, using cylinders as the basic building block instead of rectangles.
- 📐 The script explains the mathematical definition of a cylinder, highlighting that it has congruent cross-sections all the way through, with the familiar form being the right circular cylinder.
- 🔍 The lecturer discusses the fundamental assumptions for volume, drawing parallels with those for area, and notes that the volume of a cylinder is the cross-sectional area times the height.
- 📉 The script delves into the application of integral calculus to find the volume of a cone, using the method of circumscribing rectangles and taking the limit as the number of divisions approaches infinity.
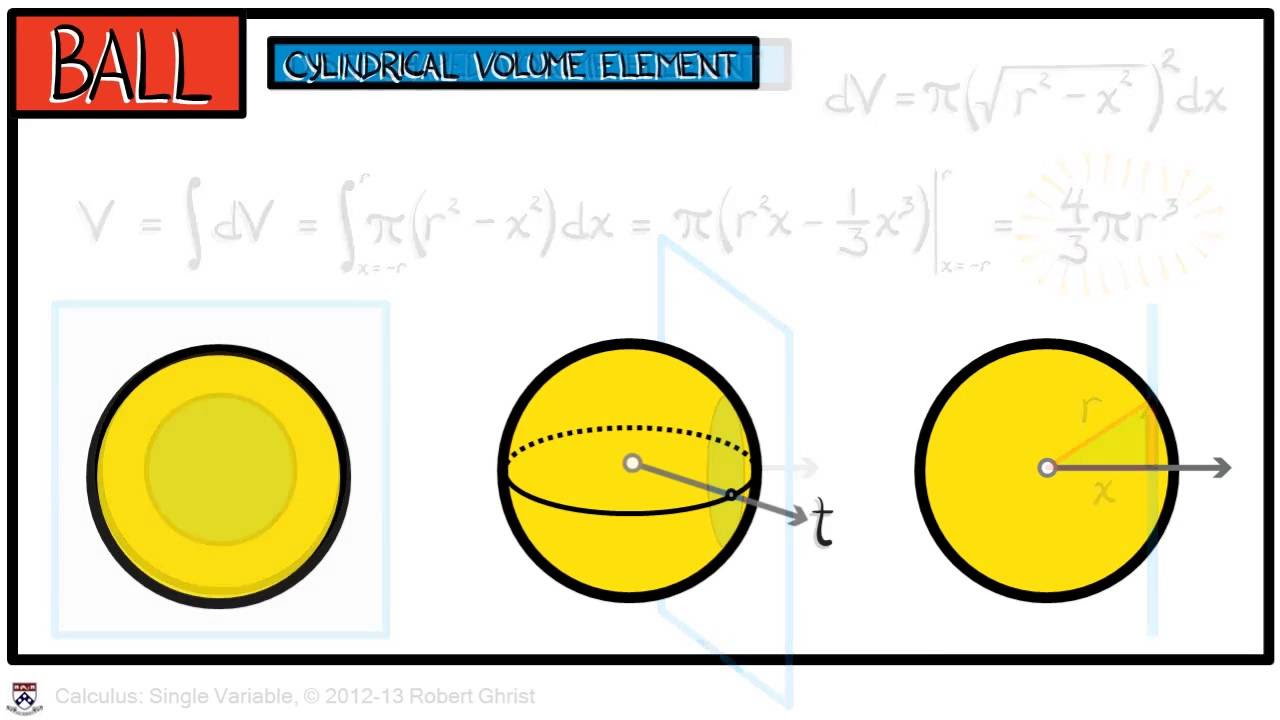
- 📈 It illustrates the process of deriving the volume of a cone using both integral and differential calculus, showing that the volume is \( \frac{1}{3} \pi r^2 h \), where \( r \) is the radius and \( h \) is the height.
- 📝 The importance of the continuity of the cross-sectional area function in determining the volume of a solid region is emphasized, as it allows for the use of definite integrals to calculate volume.
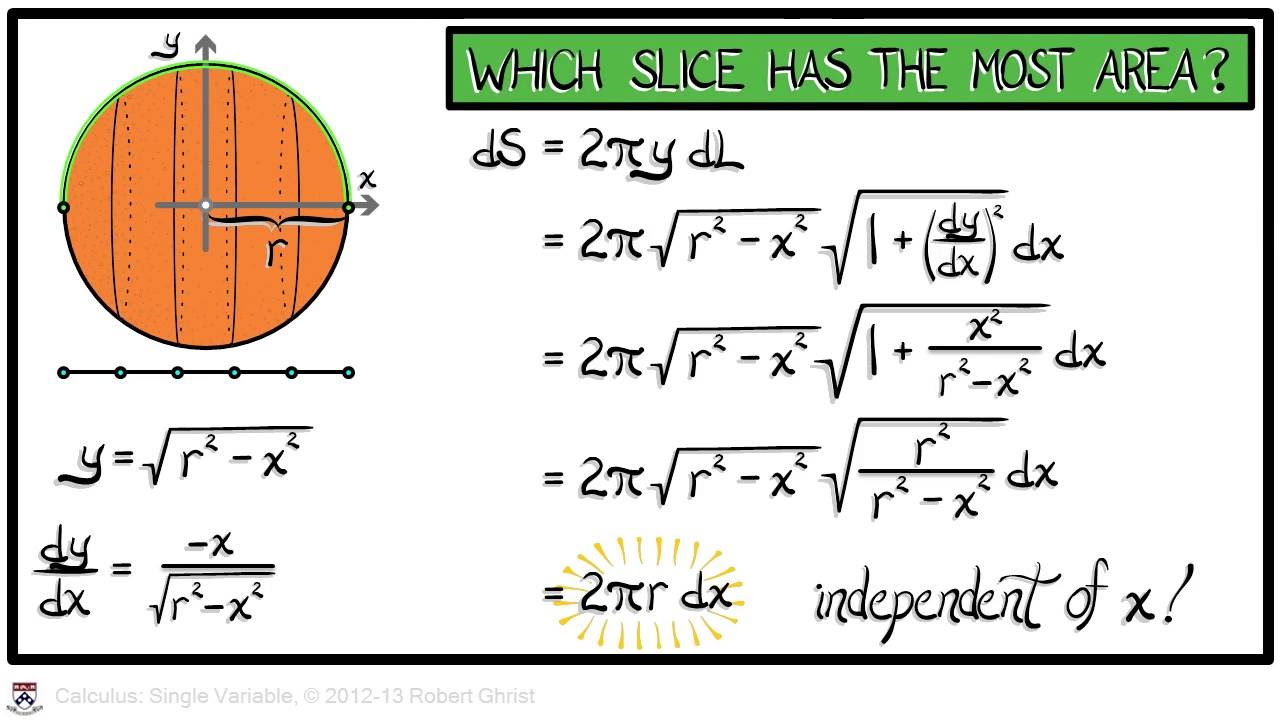
- 🌀 The concept of 'solids of revolution' is introduced, explaining how a plane area rotated around an axis generates a 3-dimensional region, and the volume of such regions can be found using integral calculus.
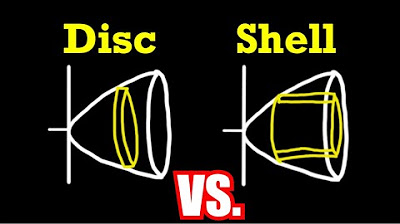
- 📦 The script covers the method of cylindrical shells, a technique used to find the volume of solids generated by revolving a region around an axis, particularly when the generating element is parallel to the axis of rotation.
- 🔄 The difference in volume generated by revolving the same area around different axes is highlighted, showing that the volume can vary depending on the axis of rotation.
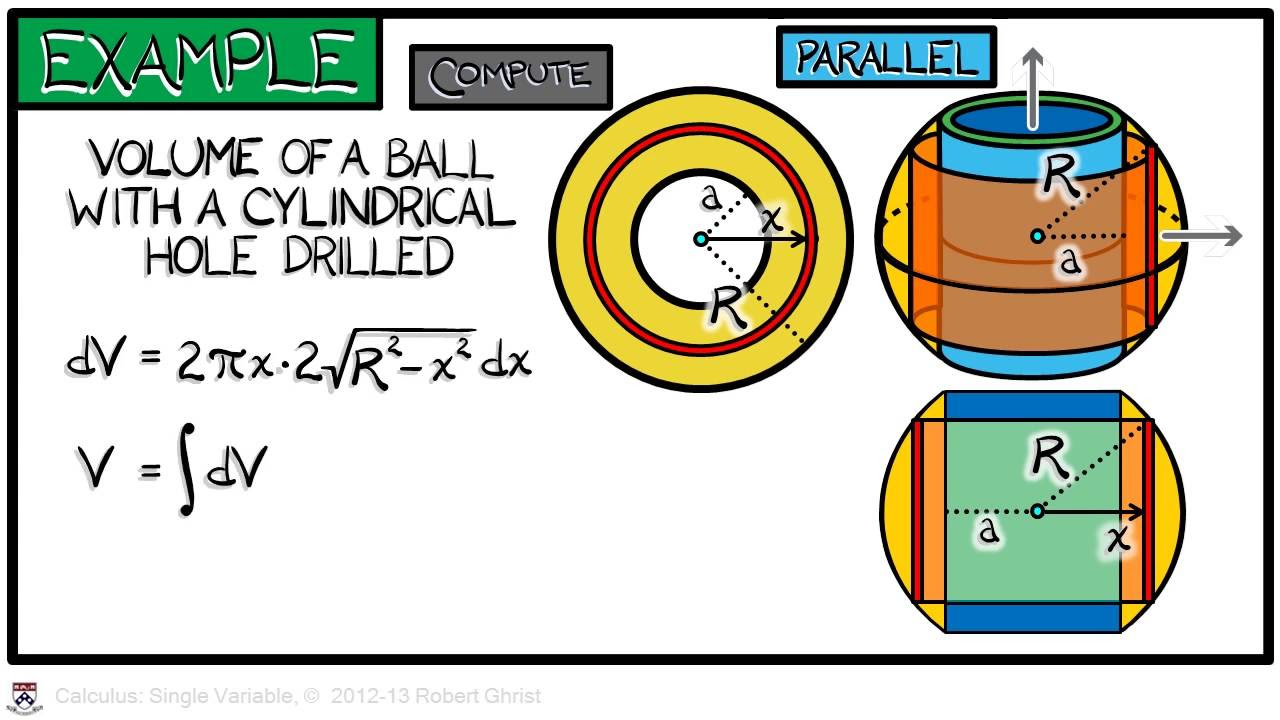
- 📘 Examples are provided to demonstrate the application of the methods discussed, including the calculation of volumes for cones and regions under curves, using both integral and differential calculus.
- 🔑 The summary of the lecture reinforces the concept that the definite integral represents the limit of a sum of products of function values and interval widths, which can be used to calculate areas, volumes, or distances in various contexts.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the application of integral calculus and differential calculus to find volumes of solid regions, emphasizing the relationship between the two subjects.
Why is the lecture titled '3-dimensional Area'?
-The lecture is titled '3-dimensional Area' to illustrate the concept of studying volumes in an analogous way to how areas are studied, highlighting the mathematical structure behind both.
What is the basic building block for volumes according to the lecture?
-The basic building block for volumes is the cylinder, as opposed to the rectangle for areas.
What are the three assumptions made for studying volume in the lecture?
-The three assumptions for studying volume are: 1) The volume of any cylinder is the cross-sectional area times the height. 2) If a three-dimensional region R is contained within another region S, then the volume of R is less than or equal to the volume of S. 3) The volume of a region made up of non-overlapping parts is the sum of the volumes of the constituent parts.
How is the volume of a right circular cylinder calculated?
-The volume of a right circular cylinder is calculated as 'pi times the radius squared times the height' (πr²h).
What method is used in the lecture to derive the volume of a cone?
-The method used to derive the volume of a cone in the lecture is by revolving a right triangle about the x-axis and using the axioms of volume to find the limit of an upper approximation as the number of divisions approaches infinity.
What is the significance of the definite integral in calculating volume?
-The definite integral signifies the volume of a solid region when the cross-sectional area is a continuous function, allowing the calculation of volume by summing infinitesimal slices of the solid.
What is the method of cylindrical shells and when is it used?
-The method of cylindrical shells is used when the generating element of the solid is parallel to the axis of rotation. It simplifies the computation of volume by considering the volume generated by thin rectangles (shells) revolving around the axis.
How does the volume of a solid change when the region is rotated about a different axis?
-The volume of a solid can change depending on the axis of rotation due to differences in the distances of the generating elements from the axis, which affects the cross-sectional areas and thus the volume generated.
What is the fundamental theorem of calculus used for in the context of this lecture?
-In the context of this lecture, the fundamental theorem of calculus is used to relate the definite integral, which sums the areas of infinitesimally thin slices, to the volume of a solid region, providing a way to calculate volume using either integral or differential calculus.
Can the method of cylindrical shells be used for any solid of revolution?
-The method of cylindrical shells can be used for any solid of revolution, but its ease of application depends on the computational simplicity it offers compared to the method of revolution, which is determined by the relationship between the variables in the problem.
What is the importance of understanding the relationship between integral and differential calculus in the context of finding volumes?
-Understanding the relationship between integral and differential calculus is important because it allows for alternative approaches to finding volumes. In some cases, one method may be more computationally feasible than the other, and knowing both provides flexibility in problem-solving.
Outlines
📚 Introduction to 3-Dimensional Area (Volume)
The paragraph introduces the concept of '3-dimensional area' as an analogous approach to studying volume, just as area was studied in two dimensions. It emphasizes the fundamental theorems of calculus and the relationship between integral and differential calculus. The lecturer, Herbert Gross, outlines the basic assumptions for volume, similar to those for area, with the cylinder replacing the rectangle as the basic building block. The volume of a right circular cylinder is highlighted as an example, with the formula being the area of the cross-section (circle) times the height. The paragraph sets the stage for deriving volumes of various shapes using calculus.
📐 Deriving the Volume of a Cone Using Axioms
This section delves into using integral calculus to derive the volume of a cone, a classic problem in calculus. The讲师 visualizes the cone by revolving a right triangle around the x-axis and uses the concept of circumscribing rectangles to approximate the volume. The讲师 then breaks down the process into steps, calculating the volume of each thin cylindrical slice and summing these to find an upper bound for the cone's volume. The讲师 uses the sum of squares formula to simplify the expression and takes the limit as the number of slices approaches infinity, arriving at the familiar formula for the volume of a cone, 1/3 * π * r^2 * h.
📉 Error Analysis in Volume Approximation
The paragraph discusses the error analysis involved in approximating the volume of a cone and extends the concept to general 3-dimensional regions. The讲师 introduces the idea of inscribed and circumscribed cylinders to bound the volume of a slice, 'delta V', between an upper and lower estimate. By analyzing the total error as the number of slices increases, the讲师 demonstrates that the difference between the upper and lower bounds approaches zero, thus validating the volume approximation. The讲师 also generalizes this method to find the volume of any 3-dimensional region with a continuous cross-sectional area function.
🌀 Solids of Revolution and Volume Calculation
This section introduces solids of revolution, where a 2-dimensional region is rotated around an axis to form a 3-dimensional shape. The讲师 explains that the volume of such solids can be found by integrating the square of the function defining the region's boundary, due to the circular cross-sections created by the rotation. The讲师 also touches on the differential calculus approach, where the volume 'V' is the integral of the cross-sectional area function from 'a' to 'b', and can be computed as 'G(b) - G(a)', with 'G' being an antiderivative of the area function.
📐 Revisiting the Cone Volume Using Differential Calculus
The paragraph revisits the calculation of the volume of a cone, but this time using differential calculus. The讲师 describes revolving a right triangle around the x-axis to form a cone and then calculating the volume of the cone by integrating the square of the linear function defining the triangle's hypotenuse. The讲师 simplifies the integral and evaluates it to obtain the volume of the cone, confirming the result obtained earlier using integral calculus.
🌟 The Method of Cylindrical Shells
This section introduces the method of cylindrical shells, an alternative approach to calculating volumes of solids of revolution when the region is revolved around the y-axis. The讲师 explains the geometric interpretation of cylindrical shells and how they can be used to approximate the volume of a solid. The讲师 also discusses the computational advantages of this method, especially when dealing with functions that are not one-to-one, and provides a step-by-step explanation of how to set up and evaluate the integral for a cylindrical shell.
📚 Volume Calculation Using Cylindrical Shells: Examples
The paragraph provides examples to illustrate the use of cylindrical shells in calculating volumes. The讲师 first revisits the right triangle and calculates the volume generated when it is revolved around the y-axis, yielding a different volume than when revolved around the x-axis. The讲师 then tackles a more complex example involving a parabolic region and demonstrates the process of setting up and evaluating the integral for the cylindrical shells, resulting in the volume of the solid formed by the rotation.
🔍 Observations on Volumes Generated by Revolving Regions
In this section, the讲师 reflects on the observations made during the calculation of volumes by revolving regions around different axes. The讲师 points out that the same region can generate different volumes depending on the axis of rotation, emphasizing the importance of the distance from the axis and the shape of the region. The讲师 also highlights the importance of understanding the underlying principles of calculus in solving these problems.
📘 Summary of Definite Integrals and Their Applications
The final paragraph summarizes the concept of definite integrals and their applications in calculating areas, volumes, and distances traveled. The讲师 explains the process of finding the limit of a Riemann sum as the partition of the interval becomes finer, which defines the definite integral. The讲师 also connects this concept to the fundamental theorem of calculus, which allows for the computation of a definite integral by finding an antiderivative of the integrand and evaluating it at the bounds of integration.
Mindmap
Keywords
💡Creative Commons license
💡MIT OpenCourseWare
💡Integral calculus
💡Differential calculus
💡Volume
💡Cylinder
💡Right circular cylinder
💡Cone
💡Solid of revolution
💡Cylindrical shells
💡Continuous function
💡Definite integral
Highlights
Introduction to the concept of '3-dimensional Area', emphasizing the study of volumes in an analogous way to areas.
Establishment of three basic assumptions for volume, with cylinders as the basic building block instead of rectangles for areas.
Explanation of the definition of a cylinder and its properties, including congruent cross-sections.
Generalization of the volume formula for any cylinder as the cross-sectional area times the height.
Discussion of the relationship between the volume of a region and its containment within another region in 3D space.
Assumption that the volume of a non-overlapping union of regions is the sum of the individual volumes.
Illustration of how the same results shown for area can be applied to volumes due to structural similarities.
Derivation of the volume of a cone using integral calculus, emphasizing the importance of the fundamental theorems.
Introduction of the method of circumscribing rectangles to approximate the volume of a cone.
Explanation of the process to find the volume of a cone using the sum of stacked cylinders and the limit process.
Use of differential calculus to derive the volume of a cone by considering the change in volume with respect to height.
Generalization of the method to find the volume of any 3D region by slicing and summing the volumes of the slices.
Introduction of the method of cylindrical shells for calculating volumes of solids generated by rotation about the y-axis.
Demonstration of the difference in volume generated by rotating a region about the x-axis versus the y-axis.
Explanation of the method to calculate the volume of a solid of revolution by integrating the square of the function representing the cross-sectional area.
Illustration of the computation of volume for a region bounded by a parabola rotated about the y-axis using cylindrical shells.
Discussion of the significance of the distance from the axis of rotation in determining the volume of the generated solid.
Summary of the lecture highlighting the use of definite integrals and differential calculus to compute volumes and areas.
Preview of upcoming lectures to explore the limitations and complexities of the methods introduced for volume calculations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: