5.1.4 Odd-Even Identities

Justin Backeberg
26 Feb 202005:35
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, Mr. Banker explores odd and even functions, explaining their graphical properties and identities. He uses examples like sine, cosine, and tangent to illustrate odd functions, and their reciprocals, showing how they behave with negative angles. He also demonstrates how to apply these identities to solve problems, such as finding the sine of an angle given the cosine.

Takeaways
  • 📚 The video discusses odd and even functions and their graphical representations.
  • 🔍 Odd functions have origin symmetry, exemplified by a cubic graph that matches up when rotated around the origin.
  • 📈 Even functions have y-axis symmetry, as seen in the graph of x squared, a parabola that aligns when folded over the y-axis.
  • 📉 Trigonometric functions like sine and tangent are odd, as their graphs match up when rotated around the origin.
  • 🌉 Cosine is an even function, as its graph has y-axis symmetry, similar to the cosine graph that extends symmetrically in both positive and negative directions.
  • 🔄 Sine is an odd function, and its reciprocal, cosecant, also exhibits odd behavior, allowing for the transformation of sine(-θ) to -sine(θ).
  • 🔄 Tangent is an odd function, and its reciprocal, cotangent, also follows the odd function rule, making tan(-θ) equal to -tan(θ).
  • 🔄 Cosine is an even function, and its reciprocal, secant, is also even, meaning sec(-θ) equals sec(θ).
  • 🔧 The video demonstrates how to use these identities to solve problems, such as finding the sine of an angle given the cosine of the same angle.
  • 📚 The final example shows how to manipulate the sine function using cofunction identities and the properties of odd and even functions to find the sine of θ - π/2 given cos(θ) = 0.34.
Q & A

  • What does it mean for a function to be odd or even?

    -A function is considered odd if its graph has origin symmetry, meaning that if you rotate the graph around the origin, the portions of the graph in the first and third quadrants will match. An even function, on the other hand, has y-axis symmetry, meaning that if you fold the graph over the y-axis, the portions in the first and second quadrants will match.

  • What is a classic example of an odd function?

    -A cubic graph is a classic example of an odd function. It exhibits origin symmetry, where rotating the graph around the origin aligns the portions in the first and third quadrants.

  • What is a classic example of an even function?

    -An x squared graph, or a parabola, is a classic example of an even function. It exhibits y-axis symmetry, where folding the graph over the y-axis aligns the portions in the first and second quadrants.

  • How does the sine function relate to odd functions?

    -The sine function is an odd function because its graph has origin symmetry. If you rotate the graph around the origin, the portions on the right-hand side will match those on the left-hand side.

  • Why is the tangent function considered odd?

    -The tangent function is considered odd because its graph has origin symmetry. It starts in the middle and goes up to the right and down to the left, similar to a cubic graph, which also exhibits origin symmetry.

  • Why is the cosine function considered even?

    -The cosine function is considered even because its graph has y-axis symmetry. If you extend the graph into the negative direction, it goes down and then comes back up, aligning with the graph in the opposite direction.

  • What happens to the sine of a negative angle in the context of odd functions?

    -For an odd function like sine, the sine of a negative angle is equal to the negative of the sine of the positive angle. This is because you can pull the negative sign out in front of the sine function.

  • How does the reciprocal of an odd function behave in terms of symmetry?

    -The reciprocal of an odd function is also odd. This is demonstrated with cosecant and cotangent, whose reciprocals (secant and tangent, respectively) also exhibit origin symmetry.

  • What happens to the cosine of a negative angle in the context of even functions?

    -For an even function like cosine, the cosine of a negative angle is equal to the cosine of the positive angle. The negative sign does not affect the value because the function exhibits y-axis symmetry.

  • How does the reciprocal of an even function behave in terms of symmetry?

    -The reciprocal of an even function is also even. This is demonstrated with secant, whose reciprocal (cosecant) also exhibits y-axis symmetry.

  • What is a cofunction identity and how is it used in the script?

    -A cofunction identity relates trigonometric functions of complementary angles. In the script, the identity is used to transform the sine of an angle into a cosine of a complementary angle, specifically by factoring out a negative and using the property of odd functions.

Outlines
00:00
📚 Understanding Odd and Even Functions

This paragraph introduces the concepts of odd and even functions in mathematics. It explains that an odd function has origin symmetry, exemplified by a cubic graph, where the graph's parts in the first and third quadrants mirror each other around the origin. An even function, on the other hand, has y-axis symmetry, as demonstrated by a parabola of an x squared function. Trigonometric functions such as sine and tangent are identified as odd due to their origin symmetry, while cosine is classified as even because of its y-axis symmetry. The reciprocal functions of sine and tangent, namely cosecant and cotangent, are also odd, whereas the reciprocal of cosine, secant, is even. The paragraph sets the stage for discussing identities related to these functions.

05:02
🔍 Applying Odd and Even Identities in Trigonometry

The second paragraph delves into the practical application of odd and even identities in trigonometry. It discusses how the sine function, being odd, allows for the simplification of expressions involving negative angles by factoring out the negative sign. Similarly, the reciprocal of sine, cosecant, follows the same rule. The tangent function, also odd, and its reciprocal, cotangent, behave in a similar fashion. In contrast, the cosine function, being even, does not change with the introduction of a negative angle, and its reciprocal, secant, maintains this property. The paragraph concludes with an example problem where the cosine of an angle is given, and the sine of the angle minus π/2 is to be found using cofunction identities and the properties of odd and even functions. The solution involves manipulating the expression to apply the known value of cosine and arriving at the final answer of negative cosine of theta, which is -0.34 in the given example.

Mindmap
Keywords
💡Odd Function
An odd function is a mathematical function that exhibits origin symmetry. This means that for every point (x, y) on the graph of the function, there is a corresponding point (-x, -y). In the video, the cubic graph is given as an example of an odd function. The concept is further illustrated by describing how rotating the graph around the origin would align the points in the first quadrant with those in the bottom left third quadrant.
💡Even Function
An even function is one that has y-axis symmetry. This implies that for every point (x, y) on the graph, there is a corresponding point (-x, y). The video uses the parabola of an x squared graph as an example, explaining that folding the graph over the y-axis would align the points in the first quadrant with those in the second quadrant.
💡Trigonometric Functions
Trigonometric functions are mathematical functions relating the angles of a triangle to the lengths of its sides. In the video, sine, cosine, and tangent functions are discussed in the context of their odd or even properties. Sine and tangent are identified as odd functions, while cosine is described as even.
💡Sine Function
The sine function is a fundamental trigonometric function that relates the ratio of the opposite side to the hypotenuse in a right-angled triangle. In the video, it is described as an odd function, meaning that sine(-θ) = -sine(θ). This property is used to derive identities and solve trigonometric equations.
💡Cosine Function
The cosine function is another basic trigonometric function that relates the ratio of the adjacent side to the hypotenuse in a right-angled triangle. The video explains that cosine is an even function, meaning that cosine(-θ) = cosine(θ). This property is crucial for understanding the symmetry of cosine graphs.
💡Tangent Function
The tangent function is defined as the ratio of the sine to the cosine of an angle. In the video, it is noted that the tangent function is an odd function, which means that tangent(-θ) = -tangent(θ). This is illustrated by the tangent graph's behavior, which resembles a cubic graph with origin symmetry.
💡Cosecant Function
Cosecant is the reciprocal of the sine function. In the video, it is mentioned that since sine is an odd function, cosecant is also odd, implying that cosecant(-θ) = -cosecant(θ). This property is used to understand the behavior of cosecant graphs and solve related equations.
💡Cotangent Function
Cotangent is the reciprocal of the tangent function. The video explains that cotangent is an odd function, similar to tangent, which means that cotangent(-θ) = -cotangent(θ). This property helps in understanding the symmetry and behavior of cotangent graphs.
💡Secant Function
Secant is the reciprocal of the cosine function. The video states that since cosine is an even function, secant is also even, meaning that secant(-θ) = secant(θ). This property is key to understanding the symmetry and behavior of secant graphs.
💡Cofunction Identities
Cofunction identities are mathematical relationships between trigonometric functions of complementary angles. In the video, an example is given where the sine of an angle minus π/2 is related to the cosine of the original angle. This identity is used to solve for unknown trigonometric values based on known values.
💡Graphical Representation
Graphical representation refers to the visual depiction of mathematical functions and their properties. The video uses graphical representation extensively to explain the concepts of odd and even functions, demonstrating how the symmetry of these functions can be visualized on a graph.
Highlights

Introduction to odd and even functions and their graphical representations.

Odd functions have origin symmetry, exemplified by the cubic graph.

Even functions have y-axis symmetry, exemplified by the parabola of x squared.

Trigonometric functions can be classified as odd or even.

Sine function is an odd function due to its symmetry around the origin.

Tangent function is an odd function, similar to a cubic graph with origin symmetry.

Cosecant is the reciprocal of sine and thus also an odd function.

Cosine function is an even function, shown by its symmetry around the y-axis.

Cotangent is the reciprocal of tangent and thus also an odd function.

Secant is the reciprocal of cosine and thus an even function.

Odd functions allow for the negative sign to be factored out in expressions like sine of negative theta.

Even functions negate the effect of the negative sign in expressions like cosine of negative theta.

Demonstration of using trigonometric identities to solve for sine of theta minus PI/2 given cosine of theta.

Factoring out a negative sign and using cofunction identities to simplify expressions.

Final solution involves recognizing the relationship between sine and cosine and applying the given value of cosine.

The video concludes with a summary of the process and the final answer.

Transcripts

Browse More Related Video

5.1.2 Pythagorean Identities

5.4.1 Double-Angle Identities

Pythagorean Identities for Trigonometric Functions (Precalculus - Trigonometry 10)

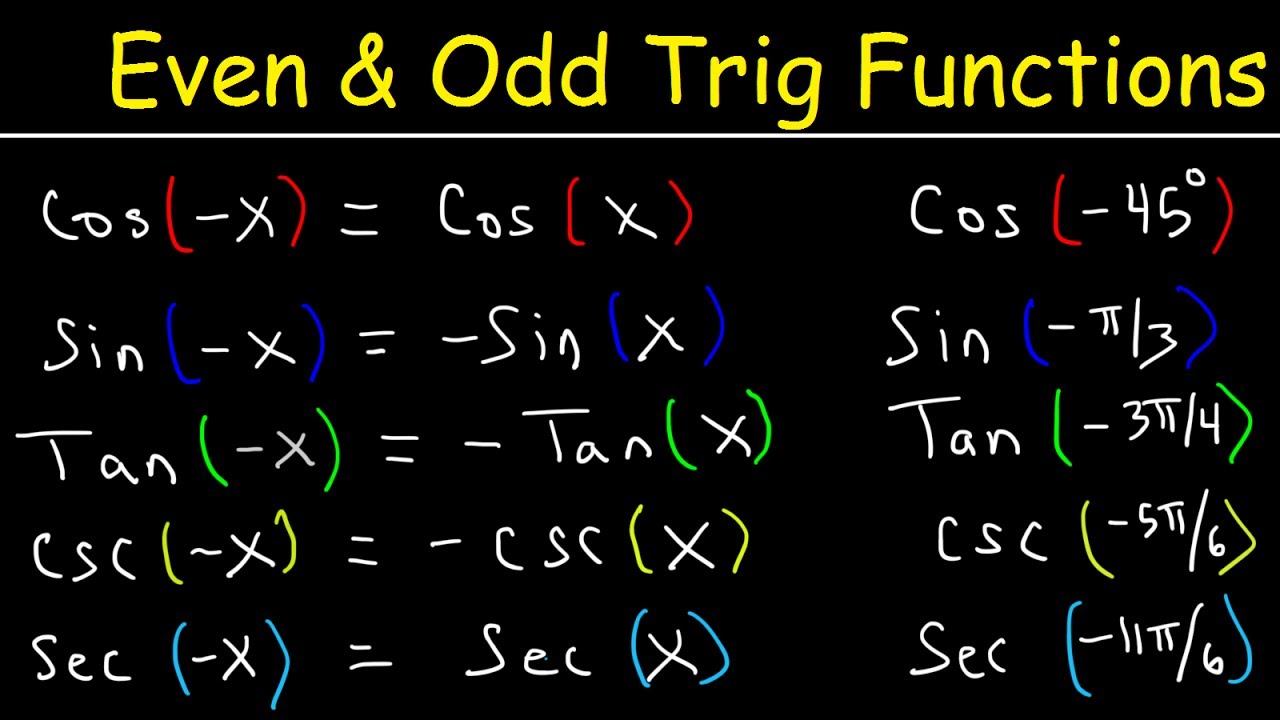
Even and Odd Trigonometric Functions & Identities - Evaluating Sine, Cosine, & Tangent

Trig - 0.4 Fundamental Trig Identities

Trig - 0.5 Periodic and Even and Odd Function Properties

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathTrigonometryOdd FunctionsEven FunctionsGraph SymmetrySineCosineTangentCofunction IdentitiesEducational