Trig - 0.5 Periodic and Even and Odd Function Properties

Kimberly Brehm

23 Jun 202107:35

EducationalLearning

32 Likes 10 Comments

TLDRThe video script offers an insightful overview of periodic functions, focusing on their properties and behavior. It explains that a function is considered periodic if its pattern repeats after adding a constant value, denoted as 'p'. The sine and cosine functions, along with their reciprocals cosecant and secant, are highlighted as having a period of 2π, meaning their patterns restart every 2π units. In contrast, the tangent and cotangent functions have a shorter period of π, restarting their patterns more frequently. The script also delves into the concepts of even and odd functions, illustrating how even functions like cosine and secant exhibit symmetry about the y-axis, while odd functions like sine and tangent are symmetric about the origin. The video concludes with practical examples, demonstrating how to find equivalent angles for cosine and tangent functions by utilizing their periods. This summary encapsulates the video's essence, providing a clear and concise understanding of periodic functions and their characteristics.

Takeaways

🔁 A periodic function repeats its values in regular intervals, called its period.
🌀 The sine (sin) and cosine (cos) functions have a period of 2π, meaning they repeat every 2π units.
📉 The tangent (tan) and cotangent (cot) functions have a period of π, repeating more frequently than sin and cos.
🔃 The cosecant (csc) and secant (sec) functions also have a period of 2π, similar to sin and cos.
🤔 Even functions, like cosine and secant, satisfy f(x) = f(-x) and are symmetrical about the y-axis.
🔄 Odd functions, such as sine and tangent, satisfy -f(x) = f(-x) and are symmetrical about the origin.
↔️ To determine the period of a function, one can add or subtract multiples of the period until the argument falls within a standard interval.
📐 For cosine, adding 2π to the argument results in the same value due to its 2π period.
➗ The period of tangent is π because it involves the ratio of sine to cosine, which changes sign when both the numerator and denominator change sign.
🚫 Tangent is undefined at odd multiples of π/2 because it involves division by zero.
🔢 The value of a trigonometric function at a large or negative multiple of π can be found by reducing the angle to a first quadrant angle using the period.
➡️ The next topic to be covered is the trigonometric functions of acute angles.

Q & A

What is a periodic function?
-A periodic function is a function that repeats its values at regular intervals or periods. If a function f(x) equals f(x + p) for every x in its domain, then it is considered periodic with period p.
What is the period of the sine function?
-The period of the sine function is 2π. This means that the sine function repeats its values every 2π units along the x-axis.
How does the cosine function's period compare with that of the sine function?
-The cosine function also has a period of 2π, which is the same as the sine function, meaning it repeats its pattern every 2π units along the x-axis.
What is the period of the tangent function?
-The period of the tangent function is π. This is because the tangent function starts repeating its pattern every π units along the x-axis.
What is an even function in terms of symmetry?
-An even function is one that is symmetric about the y-axis. This means that f(x) = f(-x) for all x in the domain of the function.
How can you determine if a function is odd?
-A function is odd if it is symmetric about the origin. This means that -f(x) = f(-x) for all x in the domain of the function.
Which trigonometric functions are considered even?
-Cosine and secant are considered even functions because they satisfy the condition f(x) = f(-x).
Which trigonometric functions are considered odd?
-Sine, tangent, cosecant, and cotangent are considered odd functions because they satisfy the condition -f(x) = f(-x).
How can you find the value of cosine for an angle that is a multiple of π?
-You can find the value of cosine for an angle that is a multiple of π by adding or subtracting 2π (which is the period of cosine) until the angle aligns with a known value on the unit circle.
What is the significance of the period of the tangent function being π?
-The period of the tangent function being π signifies that the tangent function's pattern repeats every π units. This is due to the fact that tangent is the ratio of sine to cosine, and both sine and cosine have periods of 2π, which when divided gives π.
How does the cotangent function relate to the tangent function in terms of period?
-The cotangent function has the same period as the tangent function, which is π. This is because cotangent is the reciprocal of tangent, and both functions repeat their patterns every π units along the x-axis.
What is the value of tangent at an angle of π/2 radians?
-The value of the tangent function at an angle of π/2 radians is undefined because the tangent function is the ratio of sine to cosine, and at π/2, cosine is zero, resulting in a division by zero.
How can you simplify the calculation of sine for an angle that is a multiple of π?
-You can simplify the calculation of sine for an angle that is a multiple of π by subtracting or adding 2π from the angle until it aligns with a known value on the unit circle, since the sine function has a period of 2π.

Outlines

00:00

📊 Understanding Periodic Functions and Their Properties

This paragraph introduces the concept of periodic functions, explaining that a function is considered periodic if adding a constant 'p' results in the function repeating its values indefinitely. The sine function is used as an example, with a period of 2π, meaning that after every 2π interval, the pattern of the function restarts. Cosine, secant, and cosecant are also mentioned to have a period of 2π, while tangent and cotangent have a period of π, indicating a quicker repetition of their patterns. The paragraph further explains the concepts of even and odd functions, with even functions being symmetrical about the y-axis (f(x) = f(-x)) and odd functions being symmetrical about the origin (-f(x) = f(-x)). Cosine, secant, and tangent are identified as even functions, while sine and cotangent are odd. The explanation is accompanied by practice questions to illustrate how to find equivalent angles for cosine and tangent functions based on their periods.

05:01

🔢 Applying Periodicity to Trigonometric Functions

The second paragraph delves into applying the concept of periodicity to solve trigonometric problems. It discusses how to find the values of cosine and tangent for angles that are multiples of their respective periods. For cosine, which has a period of 2π, the paragraph demonstrates that cosine of negative 7π/4 is equivalent to cosine of π/4 by adding 2π to the given angle. For tangent, which has a period of π, the paragraph explains that tangent of -π/2 can be transformed to tangent of π/2 by adding π, noting that tangent is undefined at these points due to division by zero. The paragraph concludes by simplifying the expression for sine of 17π/6 to sine of 5π/6, which can be more easily evaluated using the unit circle. The final section of the paragraph teases the topic of trigonometric functions for acute angles, which will be covered in the subsequent part of the video.

Mindmap

Keywords

💡Periodic Function

A periodic function is a type of function that repeats its values at regular intervals or periods. In the context of the video, the sine and cosine functions have a period of 2π, meaning their patterns repeat every 2π units along the x-axis. This is a central concept as it defines the behavior of many trigonometric functions.

💡Even Function

An even function is one where the value of the function remains the same when the sign of the input is changed. Formally, f(x) = f(-x). In the video, cosine and secant are identified as even functions, which can be visualized by folding their graphs along the x-axis and seeing that they coincide.

💡Odd Function

An odd function is characterized by the property that the function's sign changes when the sign of the input is changed, which can be expressed as -f(x) = f(-x). The video mentions that tangent and cosecant are odd functions, and their symmetry is about the origin, not the y-axis.

💡Sine Function

The sine function is a fundamental trigonometric function that has a periodic nature with a period of 2π. It is used in the video to illustrate the concept of periodicity, showing how the sine wave repeats its pattern every 2π units. The sine function is also identified as an odd function in the video.

💡Cosine Function

The cosine function, like the sine function, is a trigonometric function with a period of 2π. It is an even function, which means it is symmetric about the y-axis. The video uses the cosine function to demonstrate how the pattern of the function repeats every 2π units.

💡Tangent Function

The tangent function is a trigonometric function that has a period of π, not 2π like sine and cosine. It is an odd function, and its graph has vertical asymptotes where the function is undefined. The video explains that the tangent function's period is π because it is the ratio of sine to cosine.

💡Cosecant Function

Cosecant, or csc, is the reciprocal of the sine function, and like sine, it is an odd function with a period of 2π. The video mentions cosecant in the context of discussing the periods of trigonometric functions and their reciprocal identities.

💡Secant Function

Secant, or sec, is the reciprocal of the cosine function. It is an even function with a period of 2π, similar to cosine. The video briefly mentions secant when discussing the periods of trigonometric functions.

💡Asymptote

An asymptote is a line that a function approaches but never actually reaches. In the context of the video, the tangent function has asymptotes at π intervals, which are points where the function becomes undefined. The video uses the concept of asymptotes to explain the behavior of the tangent function.

💡Unit Circle

The unit circle is a circle with a radius of 1 centered at the origin, often used in the context of trigonometry to define and visualize trigonometric functions. The video refers to the unit circle when discussing the values of sine and cosine for specific angles, such as π/4 and π/6.

💡Trigonometric Functions

Trigonometric functions are mathematical functions that relate the angles of a triangle to the lengths of its sides, particularly useful in the study of triangles and periodic phenomena. The video focuses on the properties of several trigonometric functions, including their periodicity and symmetry.

Highlights

A periodic function is a function that repeats its values at regular intervals or periods

The sine function has a period of 2π

The cosine function also has a period of 2π

Cosecant and secant functions have a period of 2π as well

Tangent and cotangent functions have a period of π

An even function satisfies f(x) = f(-x) and is symmetric about the y-axis

A cosine function is an example of an even function

An odd function satisfies -f(x) = f(-x) and is symmetric about the origin

Sine, cosecant, and secant are even functions, while tangent and cotangent are odd functions

The period of a function can be found by adding or subtracting multiples of the period until the argument falls within one period

For cosine, adding 2π to the argument results in the same value

For tangent, adding π to the argument results in the same value

The tangent function has a period of π because it is the ratio of sine to cosine

The value of tangent is undefined when the cosine is 0

Sine is the y-value on the unit circle, while tangent is the ratio of sine to cosine, or y/x

The period of a function can be used to simplify trigonometric expressions

The unit circle can be used to find the values of sine and cosine for any angle

Transcripts

Browse More Related Video

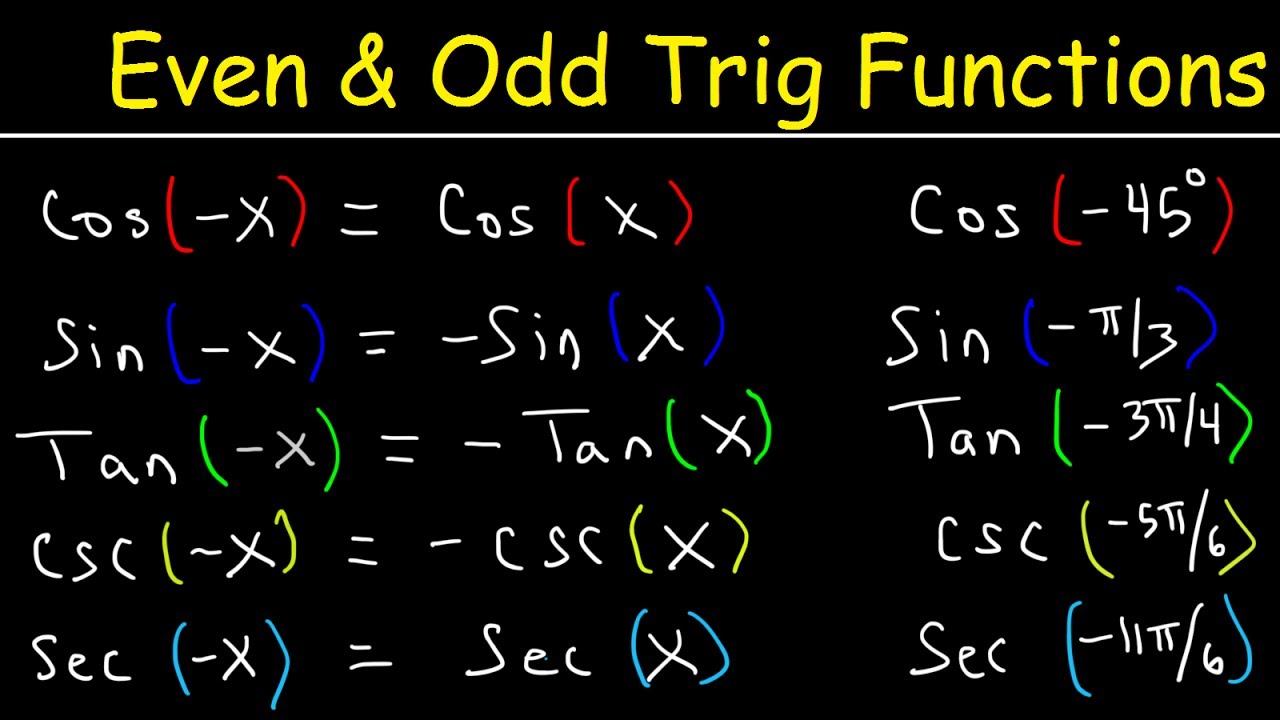
Even and Odd Trigonometric Functions & Identities - Evaluating Sine, Cosine, & Tangent

How to Graph Cosecant and Secant (Precalculus - Trigonometry 15)

Basic Properties of Trigonometric Functions (Precalculus - Trigonometry 8)

How to Graph Tangent and Cotangent (Precalculus - Trigonometry 13)

How To Evaluate Trigonometric Functions Using Periodic Properties - Trigonometry

Graphing Transformations with Tangent and Cotangent (Precalculus - Trigonometry 14)

Trig - 0.5 Periodic and Even and Odd Function Properties

Takeaways

Q & A

What is a periodic function?

What is the period of the sine function?

How does the cosine function's period compare with that of the sine function?

What is the period of the tangent function?

What is an even function in terms of symmetry?

How can you determine if a function is odd?

Which trigonometric functions are considered even?

Which trigonometric functions are considered odd?

How can you find the value of cosine for an angle that is a multiple of π?

What is the significance of the period of the tangent function being π?

How does the cotangent function relate to the tangent function in terms of period?

What is the value of tangent at an angle of π/2 radians?

How can you simplify the calculation of sine for an angle that is a multiple of π?