Trig - 0.4 Fundamental Trig Identities

Kimberly Brehm
23 Jun 202107:19
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides an in-depth exploration of fundamental trigonometric identities, focusing on reciprocal and quotient identities. It begins by explaining that sine is equivalent to the reciprocal of cosecant, and secant is the reciprocal of cosine, with tangent and cotangent being reciprocals as well. The script then illustrates how to apply these identities using an example involving a right triangle with given sine and cosine values, showing how to calculate tangent and cosecant. It also covers the Pythagorean identities, which relate the squares of sine and cosine, and uses these to solve for tangent given the secant of an angle. The video concludes with a practice problem that simplifies an expression involving sine and cosecant. The script is designed to be engaging, using visual aids like the unit circle and right triangle to help viewers understand the concepts.

Takeaways
  • 📐 **Reciprocal Identities**: Sine is the reciprocal of cosecant (sin(θ) = 1/cosec(θ)), and cosine is the reciprocal of secant (cos(θ) = 1/sec(θ)).
  • 🔁 **Tangent and Cotangent Reciprocity**: Tangent and cotangent are reciprocal functions (tan(θ) = sin(θ)/cos(θ) and cot(θ) = cos(θ)/sin(θ)).
  • 📐 **Right Triangle Visualization**: Understanding sine and cosine as opposite over hypotenuse and adjacent over hypotenuse, respectively, helps visualize right triangles.
  • 🔢 **Sine and Cosine Values**: Given sin(θ) = 15/17 and cos(θ) = 8/17, the tangent of theta can be found by dividing these two values.
  • 📏 **Cosecant Calculation**: Cosecant of theta is calculated as the reciprocal of sine, which in the given example is 17/15.
  • 🔴 **Tangent and Cosecant in Quadrants**: In the fourth quadrant, tangent is negative because sine (opposite/hypotenuse) is negative while cosine (adjacent/hypotenuse) is positive.
  • 🧮 **Pythagorean Identities**: The sum of sine squared and cosine squared equals one (sin²(θ) + cos²(θ) = 1), which is fundamental in trigonometry.
  • 🔢 **Secant and Tangent Relationship**: Tangent squared plus one equals secant squared (tan²(θ) + 1 = sec²(θ)), which can be used to find the tangent of an angle.
  • 🔍 **Domain Consideration**: When solving for trigonometric functions, the domain (range of possible values of the variable) is crucial, as it affects the sign of the result.
  • ➗ **Simplification Using Identities**: Simplifying expressions using trigonometric identities, such as replacing 1 - cos²(θ) with sin²(θ), can streamline calculations.
  • 📈 **Function Properties**: Trigonometric functions have properties like periodicity and being even or odd, which are important for understanding their behavior across different angles.
Q & A

  • What are the reciprocal identities in trigonometry?

    -The reciprocal identities in trigonometry are sine being the reciprocal of cosecant, secant being the reciprocal of cosine, and tangent being the reciprocal of cotangent.

  • What is the relationship between sine and cosine in terms of tangent?

    -Tangent is defined as the ratio of sine to cosine, or tan(θ) = sin(θ) / cos(θ).

  • How can you find the value of tangent given sine and cosine values of a right triangle?

    -You can find the value of tangent by dividing the sine value by the cosine value, i.e., if sin(θ) = 15/17 and cos(θ) = 8/17, then tan(θ) = (15/17) / (8/17) = 15/8.

  • What is the definition of cosecant in terms of sine?

    -Cosecant is the reciprocal of sine, which means if sin(θ) = 15/17, then csc(θ) = 1 / sin(θ) = 17/15.

  • What are the Pythagorean identities in trigonometry?

    -The Pythagorean identities are: sin²(θ) + cos²(θ) = 1, tan²(θ) + 1 = sec²(θ), and 1 + cot(θ) = csc²(θ).

  • How can you use the Pythagorean identity to find the value of tangent if you are given the value of secant?

    -If sec(θ) = √(11/3), you can use the identity tan²(θ) + 1 = sec²(θ) to find tan(θ). By squaring the secant value and subtracting 1, you get tan²(θ) = 11 - 1 = 10, and taking the square root gives tan(θ) = ±√(10/3).

  • Which quadrant on the unit circle corresponds to a negative tangent value?

    -The second and fourth quadrants on the unit circle correspond to negative tangent values because in these quadrants, sine is negative while cosine is positive (second quadrant) or sine is positive while cosine is negative (fourth quadrant).

  • How can you determine the sign of the tangent value for an angle θ in the fourth quadrant?

    -In the fourth quadrant, the x-value (corresponding to cosine) is positive, and the y-value (corresponding to sine) is negative. Therefore, the tangent, which is sine over cosine, will be negative.

  • What is the relationship between 1 - cos²(θ) and csc(θ) in terms of simplification?

    -Using the Pythagorean identity sin²(θ) + cos²(θ) = 1, we can rearrange to sin²(θ) = 1 - cos²(θ). Since csc(θ) is the reciprocal of sin(θ), the expression simplifies to csc(θ) * sin(θ), which further simplifies to sin(θ).

  • What are the periodic and even and odd function properties in trigonometry?

    -The properties will be discussed in the next part of the video, but typically, periodic functions repeat their values at regular intervals, while even functions are symmetric about the y-axis and odd functions are symmetric about the origin.

  • How can the reciprocal identities help in simplifying trigonometric expressions?

    -Reciprocal identities allow you to switch between different trigonometric functions, which can simplify expressions or make them easier to solve by converting them into more manageable forms.

  • What is the significance of the right triangle in understanding trigonometric identities?

    -The right triangle provides a geometric interpretation of the trigonometric functions, where sine represents the opposite side over the hypotenuse, cosine represents the adjacent side over the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side. This helps in visualizing and understanding the relationships between these functions.

Outlines
00:00
📐 Reciprocal and Quotient Trigonometric Identities

The first paragraph introduces the fundamental trigonometric identities, focusing on reciprocal and quotient identities. It explains that sine is the reciprocal of cosecant, secant is the reciprocal of cosine, and tangent and cotangent are reciprocals of each other. The paragraph also covers the identity of tangent being sine over cosine and vice versa for cotangent. A practice example is provided to illustrate how to use these identities to find the tangent and cosecant of an angle given the sine and cosine values of a right triangle. The right triangle's properties are used to validate the results obtained through the identities. Additionally, the Pythagorean identities are introduced, which relate the squares of sine and cosine, tangent and secant, and cotangent and cosecant.

05:00
🧮 Applying Pythagorean Identities to Find Tangent

The second paragraph delves into the application of Pythagorean identities to solve for the tangent of an angle. Given the secant of an angle, the paragraph demonstrates how to use the identity that equates tangent squared plus one to secant squared to find the tangent. The process involves squaring the given secant value, substituting it into the identity, and solving for the tangent, which results in a positive or negative square root. The paragraph also discusses the importance of considering the angle's quadrant to determine the sign of the tangent value. A further practice problem simplifies an expression involving sine and cosecant by using the Pythagorean identity and algebraic manipulation. The summary concludes with a mention of upcoming topics on periodic and even-odd function properties.

Mindmap
Keywords
💡Reciprocal Identities
Reciprocal identities in trigonometry refer to the relationships between the trigonometric functions where one function is the reciprocal of another. In the video, it is mentioned that sine is the reciprocal of cosecant (sin(θ) = 1/cosec(θ)), and cosine is the reciprocal of secant (cos(θ) = 1/sec(θ)). These identities are fundamental for simplifying trigonometric expressions and are central to the video's theme of exploring fundamental trigonometric identities.
💡Quotient Identities
Quotient identities are used to express one trigonometric function as the quotient of two other trigonometric functions. The video explains that tangent is sine divided by cosine (tan(θ) = sin(θ)/cos(θ)), and cotangent is the reciprocal, or cosine divided by sine (cot(θ) = cos(θ)/sin(θ)). These identities are key to understanding the relationships between the different trigonometric functions and are demonstrated through examples in the video.
💡Right Triangle
A right triangle is a triangle with one angle being 90 degrees. In the context of the video, the right triangle is used to visually represent the relationship between sine, cosine, and tangent through the sides of the triangle, specifically the opposite, adjacent, and hypotenuse. The script uses the example of a right triangle with sine of theta being 15/17 and cosine of theta being 8/17 to illustrate the concept of tangent.
💡Pythagorean Identities
Pythagorean identities are fundamental relationships in trigonometry that are derived from the Pythagorean theorem. The video mentions three such identities: sin²(θ) + cos²(θ) = 1, tan²(θ) + 1 = sec²(θ), and 1 + cot(θ) = csc(θ). These identities are crucial for the video's discussion on simplifying trigonometric expressions and are used in a practice question to find the value of tangent given the secant of theta.
💡Tangent
The tangent function, often abbreviated as tan, is a trigonometric function that relates the ratio of the opposite side to the adjacent side in a right triangle. In the video, tangent is used in multiple contexts, including the reciprocal identity with cotangent and in a practice problem where the value of tangent is found given the value of secant. The video also explains that tangent can be negative depending on the quadrant in which the angle θ lies.
💡Cosecant
Cosecant, represented as csc or cosec, is a reciprocal trigonometric function, which is the reciprocal of the sine function (csc(θ) = 1/sin(θ)). It is used in the video to demonstrate the reciprocal identity and to find the value of cosecant given the value of sine in a right triangle. The concept is also related to the hypotenuse and the opposite side in the context of a right triangle.
💡Secant
Secant, denoted as sec, is another reciprocal trigonometric function, which is the reciprocal of the cosine function (sec(θ) = 1/cos(θ)). The video discusses secant in relation to the cosine function and uses it in a practice problem involving the pythagorean identity to find the value of tangent.
💡Cotangent
Cotangent, abbreviated as cot, is a reciprocal trigonometric function that is the reciprocal of the tangent function (cot(θ) = 1/tan(θ)). It is also expressed as the ratio of cosine to sine (cot(θ) = cos(θ)/sin(θ)). In the video, cotangent is used to illustrate the reciprocal identities and its relationship with tangent.
💡Sine Function
The sine function, represented as sin, is a fundamental trigonometric function that in a right triangle, represents the ratio of the length of the side opposite the angle to the length of the hypotenuse. The video uses the sine function to explain the reciprocal identity with cosecant and to calculate the tangent of an angle in a given right triangle.
💡Cosine Function
The cosine function, denoted as cos, is a trigonometric function that corresponds to the ratio of the adjacent side to the hypotenuse in a right triangle. The video discusses the cosine function in the context of its reciprocal identity with secant and its use in finding the tangent of an angle through the quotient identity with sine.
💡Unit Circle
The unit circle is a circle with a radius of 1 unit, centered at the origin of a coordinate plane. It is used in the video to describe the behavior of the tangent function in different quadrants, particularly noting that in the fourth quadrant, where x is positive and y is negative, the tangent will be negative. The unit circle is a fundamental concept in trigonometry that helps in understanding the signs of trigonometric function values for different angles.
Highlights

The video covers fundamental trigonometric identities, including reciprocal and quotient identities.

Sine is the reciprocal of cosecant, and secant is the reciprocal of cosine.

Cotangent and tangent are reciprocals of each other.

Tangent is defined as sine over cosine, and cotangent as cosine over sine.

The video provides a practice example using the reciprocal identities with a right triangle.

The Pythagorean identities are introduced: sin^2θ + cos^2θ = 1, tan^2θ + 1 = sec^2θ, and 1 + cotθ = cscθ.

A practice question demonstrates using the Pythagorean identity to find the tangent of an angle given the secant.

The video explains how to use the Pythagorean identity to solve for the tangent function.

The unit circle is used to determine the sign of the tangent function based on the quadrant of the angle.

The video simplifies the expression 1 - cos^2θ using the Pythagorean identity to find it equals sin^2θ * cscθ.

The video shows how to further simplify the expression to sinθ.

The reciprocal identities are used to define the cosecant as the hypotenuse over the opposite side of a right triangle.

The tangent of an angle is calculated by dividing the sine by the cosine of the angle.

The video provides a visual representation of a right triangle to help understand the relationship between the trig functions.

The Pythagorean identities are derived from the Pythagorean theorem applied to a right triangle.

The video demonstrates algebraic manipulation of the Pythagorean identities to solve for different trig functions.

The video explains the concept of even and odd functions and their properties in the context of trigonometry.

The video concludes with a summary of the key takeaways and a preview of upcoming topics on periodic functions.

Transcripts

Browse More Related Video

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)

30-60-90 Triangles - Special Right Triangle Trigonometry

Trig - 0.6 Trig Functions of Acute Angles

Proving Trigonometric Identities | Fundamental Trigonometric Identities | Formulas | Part 2

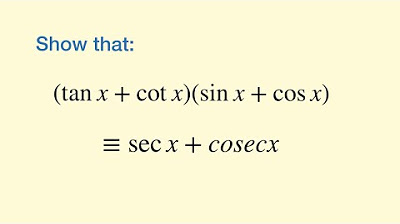
Secant, Cosecant and Cotangent - (2 of 4: Trigonometric Identities)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryMath EducationStudy GuideReciprocal IdentitiesQuotient IdentitiesPythagorean IdentitiesMath PracticeVideo TutorialEducational ContentSecondary Education