Using the Ratio Test to Determine if a Series Converges #1

patrickJMT
3 Apr 200807:39
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script introduces the Ratio Test, a valuable method for determining the convergence or divergence of series, particularly useful with power series. The test involves comparing the limit of the ratio of successive terms to 1. If the limit is less than 1, the series is absolutely convergent; if greater than 1 or infinity, it diverges. A limit equal to 1 does not provide a conclusion, necessitating alternative methods. The script demonstrates the application of the Ratio Test to two series examples, showing the process of simplification and limit evaluation to reach conclusions about their convergence.

Takeaways
  • 📊 The ratio test is a useful method for determining the convergence or divergence of a series.
  • 🔄 The test involves replacing \( n \) with \( n+1 \) in the series terms and then dividing by the original terms.
  • 📉 If the limit of the ratio as \( n \) approaches infinity is less than 1, the series is convergent.
  • 📈 If the limit is greater than 1 or infinity, the series is divergent.
  • ⚠️ If the limit equals 1, no conclusion can be made, and a different test must be used.
  • 🔢 Applying the ratio test to a series with \( \frac{n^2}{2^n} \) shows that the series converges because the limit is \( \frac{1}{2} \), which is less than 1.
  • ➗ Simplifying the terms involves cancelling common factors and focusing on the highest power terms.
  • ✔️ Another example with the series \( \frac{n(-3)^n}{4^{n-1}} \) also shows convergence as the limit is \( \frac{3}{4} \), which is less than 1.
  • 📐 When dealing with rational functions in the series, the limit is determined by the ratio of the leading coefficients of the highest power terms.
  • ⏩ A follow-up video will cover additional examples of using the ratio test for determining series convergence or divergence.
Q & A

  • What is the ratio test for series?

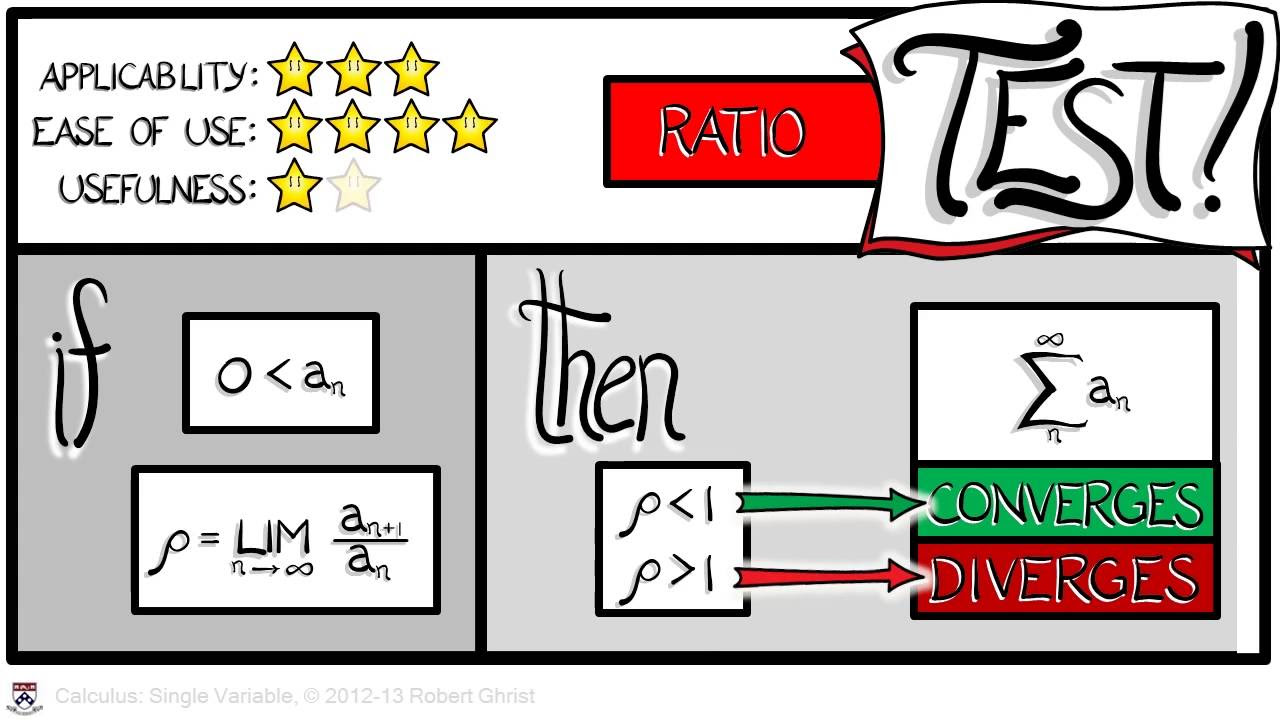
    -The ratio test for series is a method used to determine whether a series converges or diverges. It involves taking the limit of the ratio of the (n+1)th term to the nth term of the series as n approaches infinity.

  • How is the ratio test applied to a series?

    -The ratio test is applied by replacing every instance of 'n' in the series with 'n+1', then dividing the resulting expression by the original term of the series, and taking the limit as n approaches infinity.

  • What does the ratio test tell us about the convergence of a series?

    -If the limit obtained from the ratio test is less than 1, the series is absolutely convergent. If the limit is greater than 1 or approaches infinity, the series is divergent. If the limit equals 1, the test is inconclusive and a different method must be used to determine convergence.

  • What is the significance of the limit being less than 1 in the ratio test?

    -A limit less than 1 indicates that the terms of the series are decreasing in size and approaching zero, which is a condition for convergence.

  • What does it mean if the limit from the ratio test is greater than 1 or infinity?

    -If the limit is greater than 1 or infinity, it suggests that the terms of the series are not decreasing and the series is not converging, thus it is divergent.

  • Why is the ratio test inconclusive when the limit equals 1?

    -When the limit equals 1, it does not provide enough information to determine whether the series converges or diverges, so an alternative test or method is needed.

  • Can you provide an example of applying the ratio test from the script?

    -Yes, the script applies the ratio test to the series ∑(n^2 / 2^n). After simplifying the ratio of the (n+1)th term to the nth term, the limit as n approaches infinity is found to be 1/2, which is less than 1, indicating the series is convergent.

  • What is the result of applying the ratio test to the series ∑(n * (-3)^n / 4^(n-1))?

    -Upon applying the ratio test, the limit as n approaches infinity for the series ∑(n * (-3)^n / 4^(n-1)) is found to be 3/4, which is less than 1, hence the series is convergent.

  • What happens when you factor out a constant in the ratio test?

    -When a constant is factored out in the ratio test, it can be taken outside the limit expression and does not affect the limit's value, allowing for easier simplification of the expression.

  • What is the trick mentioned in the script for rational functions when taking the limit?

    -The trick for rational functions in the ratio test is to consider the ratio of the coefficients of the highest power terms when the powers are the same. This ratio gives the value of the limit as n approaches infinity.

  • Will there be a follow-up video to the one described in the script?

    -Yes, the script mentions a follow-up video where more examples of the ratio test for series will be discussed, including additional cases of convergence and divergence.

Outlines
00:00
📚 Introduction to the Ratio Test for Series

This paragraph introduces the ratio test, a mathematical tool used to determine the convergence or divergence of a series. The test involves replacing every instance of 'N' in the series with 'N+1', then dividing by the original term. If the limit of this ratio as 'N' approaches infinity is less than 1, the series is absolutely convergent. If the limit is greater than 1 or approaches infinity, the series is divergent. If the limit equals 1, the test is inconclusive, and a different method must be used. The speaker demonstrates the application of the ratio test with an example series, simplifying the terms and calculating the limit to show that the series converges, as the resulting limit is 1/2, which is less than 1.

05:00
🔍 Applying the Ratio Test to Different Series

In this paragraph, the speaker applies the ratio test to another series involving negative exponents and powers. The process involves taking the limit as 'N' approaches infinity, substituting 'N+1' for 'N', and simplifying the resulting expression. The speaker simplifies the terms and factors out constants, ultimately calculating the limit to be 3/4, which is less than 1, indicating that this series is also convergent. The speaker mentions that a follow-up video will be posted to further explore the ratio test with more examples, suggesting that the current video is part of a series on this topic.

Mindmap
Keywords
💡Ratio Test
The Ratio Test is a fundamental concept in calculus used to determine the convergence or divergence of an infinite series. It involves taking the limit of the absolute value of the ratio of the (n+1)th term to the nth term of the series as n approaches infinity. In the video, the Ratio Test is the central theme, and the script explains how it can be used to assess the convergence of series, particularly in conjunction with power series.
💡Convergent
A series is said to be convergent if the sum of its terms approaches a finite limit as the number of terms increases indefinitely. In the context of the video, the Ratio Test is used to identify if a series is convergent by checking if the limit of the ratio of successive terms is less than 1.
💡Divergent
A series is divergent if it does not converge, meaning the sum of its terms does not approach a finite limit as the number of terms increases. The script uses the Ratio Test to determine divergence by showing that if the limit of the ratio of successive terms is greater than 1 or equals infinity, the series is divergent.
💡Absolute Convergence
Absolute convergence refers to the property of a series where the series of the absolute values of its terms also converges. Although the script mentions absolute convergence in passing, it primarily focuses on using the Ratio Test to establish regular convergence.
💡Limit
In mathematics, a limit is the value that a function or sequence approaches as the input or index approaches some value. The Ratio Test specifically involves taking the limit of a certain expression as n approaches infinity, which is a key step in determining the nature of the series.
💡Power Series
A power series is an infinite series whose terms are expressions of the form anx^n, where a is a constant and x is the variable. The script mentions that the Ratio Test is often used in conjunction with power series, indicating its relevance in various mathematical contexts.
💡Rational Function
A rational function is a ratio of two polynomials. In the context of the video, when simplifying the expression obtained from the Ratio Test, the script suggests thinking of it as a rational function and taking the ratio of the coefficients of the highest powers of n to find the limit.
💡Coefficients
In the context of polynomials and series, coefficients are the numerical factors that multiply the variables raised to various powers. The script uses the term when discussing how to find the limit by taking the ratio of coefficients in a rational function derived from the Ratio Test.
💡Simplification
Simplification in mathematics refers to making a complex expression or equation more straightforward. The script demonstrates simplification when calculating the Ratio Test, by canceling out terms and factoring out constants to make the limit easier to evaluate.
💡Reciprocal
The reciprocal of a number is 1 divided by that number. In the script, the concept of reciprocals is used when explaining that dividing by the original term is equivalent to multiplying by its reciprocal, which simplifies the process of applying the Ratio Test.
💡Factor Out
To factor out in mathematics means to express a common factor in a product or sum outside of parentheses. The script mentions factoring out constants when simplifying expressions in the Ratio Test, which helps in evaluating the limit more efficiently.
Highlights

Introduction to the ratio test for series, an essential tool for determining the convergence or divergence of series, especially in conjunction with power series.

Explanation of the ratio test procedure: replacing N with N+1 in the series and dividing by the original term to find the limit as n approaches infinity.

Condition for convergence: if the limit is less than 1, the series is absolutely convergent.

Condition for divergence: if the limit is greater than 1 or infinity, the series is divergent.

Indeterminate case: if the limit equals 1, the ratio test is inconclusive and a different method is needed.

Application of the ratio test to a specific series with terms involving n, n+1, and powers of 2.

Simplification of the ratio test expression by multiplying by the reciprocal and factoring out constants.

Use of rational function limit properties to determine the limit of the simplified expression.

Conclusion that the series of N squared over 2 to the power of N is convergent based on the ratio test result.

Demonstration of applying the ratio test to a second series involving n, negative 3 raised to the power of N, and 4 to the power of N-1.

Simplification of the second series' ratio test expression, focusing on the powers of 4 and negative 3.

Cancellation of terms and factoring out of constants to simplify the ratio test expression further.

Determination of the limit for the second series, resulting in a value less than 1, indicating convergence.

Announcement of a follow-up video to explore more ratio test applications for series convergence or divergence.

Note on the video's time constraint and the decision to continue the topic in a subsequent video.

Transcripts

Browse More Related Video

Ratio Test

The Ratio Test

Ratio Test for Convergence | MIT 18.01SC Single Variable Calculus, Fall 2010

The Root Test

Calculus Chapter 5 Lecture 52 Convergence Tests 2

Ratio Test

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Ratio TestSeries ConvergenceMathematicsEducationalCalculusLimit AnalysisAbsolute ConvergenceVideo TutorialMath PracticeSeries DivergenceHigher Math