The Ratio Test

Mathispower4u
3 Oct 201009:04
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial introduces the ratio test for determining the convergence of an infinite series. It explains that if the limit of the absolute value of successive terms' ratio is less than one, the series converges, and if greater than one or approaching infinity, it diverges. The test is particularly useful for series involving exponentials or factorials. The video demonstrates the test with examples, including series with exponential and factorial terms, showing step-by-step simplifications and the final determination of convergence or divergence.

Takeaways
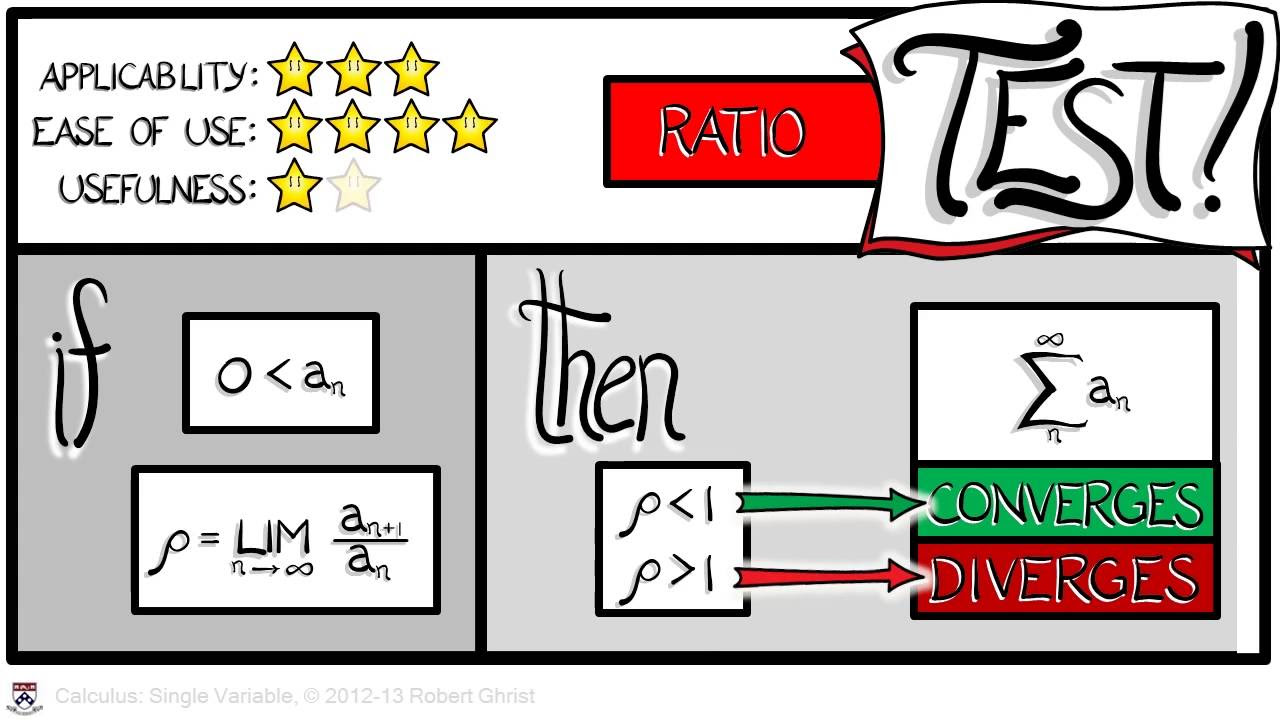
  • 📘 The ratio test determines the convergence of an infinite series with positive terms.
  • 📉 If the limit of the ratio of successive terms is less than one, the series converges.
  • 📈 If the limit is greater than one or approaches infinity, the series diverges.
  • ❌ If the limit is equal to one, the ratio test is inconclusive.
  • 🔢 The ratio test is particularly useful for series involving exponentials or factorials.
  • ➗ To apply the ratio test, compute the limit of the absolute value of the ratio of successive terms.
  • 📏 Simplification often involves canceling out common factors in the numerator and denominator.
  • 0️⃣ If the limit as N approaches infinity is zero, the series converges.
  • 🔄 For alternating series, the negative signs can be ignored when applying the ratio test.
  • 🧮 Properly handling factorials and exponential terms is crucial for accurate application of the ratio test.
Q & A

  • What is the ratio test used for in the context of infinite series?

    -The ratio test is used to determine the convergence of an infinite series with positive terms by examining the limit of the absolute value of the ratio of consecutive terms as they approach infinity.

  • What is the condition for convergence of an infinite series according to the ratio test?

    -An infinite series converges if the limit of the absolute value of the ratio of consecutive terms is less than one.

  • What happens if the limit of the ratio is greater than one?

    -If the limit of the ratio is greater than one, the series diverges according to the ratio test.

  • What does it mean if the limit of the ratio approaches positive infinity?

    -If the limit of the ratio approaches positive infinity, it indicates that the series diverges.

  • When does the ratio test fail to determine the convergence of a series?

    -The ratio test fails when the limit of the ratio is exactly equal to one.

  • In the script, which mathematical functions are mentioned as often helpful for the ratio test?

    -The script mentions that the ratio test is often helpful when the series involves exponentials or factorials.

  • How is A sub N plus one related to A sub N in the context of the ratio test?

    -In the ratio test, A sub N plus one is the term following A sub N, and the test involves taking the limit of the absolute value of A sub N plus one divided by A sub N as N approaches infinity.

  • What is the simplified form of the ratio when A sub N is four to the Nth divided by N factorial?

    -The simplified form of the ratio, when A sub N is four to the Nth divided by N factorial, is four over N plus one, as N approaches infinity, which simplifies to zero.

  • What does the ratio test indicate about the series involving N times five fourths to the Nth power?

    -The ratio test indicates that the series involving N times five fourths to the Nth power diverges because the limit of the ratio of consecutive terms is five fourths, which is greater than one.

  • In the alternating series example, how is the negative sign handled when applying the ratio test?

    -In the alternating series example, the negative sign is ignored when applying the ratio test because the absolute value of the ratio is considered.

  • What is the conclusion of the ratio test for the series involving two to the power of three N over two N factorial?

    -The ratio test concludes that the series involving two to the power of three N over two N factorial converges because the limit of the ratio approaches zero, which is less than one.

Outlines
00:00
📚 Introduction to the Ratio Test for Series Convergence

The video introduces the ratio test, a mathematical tool used to determine the convergence of an infinite series with positive terms. The test involves taking the limit of the absolute value of the ratio of consecutive terms (A sub N plus one over A sub N) as N approaches infinity. If this limit (L) is less than one, the series converges; if greater than one, it diverges; and if equal to one, the test is inconclusive. The video uses the example of a series involving exponentials and factorials to demonstrate the test's application, showing how to simplify the ratio to find the limit and determine convergence.

05:00
🔍 Applying the Ratio Test to Different Series

This paragraph explores the application of the ratio test to different series, starting with a series involving powers of four and factorials, which converges as the limit approaches zero. The video then examines a series with terms involving powers of five-fourths, demonstrating that the limit of the ratio is greater than one, indicating divergence. Finally, an alternating series with terms involving powers of two and factorials is considered, where simplification leads to a limit of zero, confirming the series' convergence. The video concludes by summarizing the key points of the ratio test and its outcomes for series convergence.

Mindmap
Keywords
💡Ratio Test
The Ratio Test is a method used in calculus to determine the convergence of an infinite series. It involves taking the limit of the absolute value of the ratio of consecutive terms of the series as the number of terms approaches infinity. In the video, the Ratio Test is the central theme, used to analyze the convergence of different series, such as those involving exponentials and factorials.
💡Convergence
Convergence refers to the property of an infinite series where the sum of its terms approaches a finite value as the number of terms increases without bound. The video explains that if the limit determined by the Ratio Test is less than one, the series converges, which is a key concept demonstrated through various examples.
💡Divergence
Divergence is the opposite of convergence and describes a series where the sum of its terms does not approach a finite value. In the context of the video, if the Ratio Test's limit is greater than one or approaches infinity, the series is said to diverge, as shown in the example with the series involving powers of five-fourths.
💡Limit
A limit in mathematics is the value that a function or sequence approaches as the input or index approaches some value. In the script, the limit is used to describe the behavior of the ratio of consecutive terms in an infinite series as the number of terms approaches infinity, which is crucial for applying the Ratio Test.
💡Factorials
A factorial, denoted by an exclamation point (e.g., N!), is the product of all positive integers up to a given number N. In the video, factorials are used in the series' terms, and their properties are utilized to simplify the expressions when applying the Ratio Test, as seen in the series with terms involving four to the power of N over N factorial.
💡Exponentials
Exponentials refer to expressions of the form a^b, where 'a' is the base and 'b' is the exponent. The video mentions that the Ratio Test is often helpful when dealing with series that involve exponential terms, as in the first example where the series has terms of four to the power of N.
💡Absolute Value
The absolute value of a number is its distance from zero on the number line, denoted by vertical bars (e.g., |x|). In the context of the Ratio Test, the absolute value ensures that the ratio is considered without regard to the sign of the terms, which is important for series that may involve alternating signs, as mentioned in the video.
💡Leading Coefficients
Leading coefficients are the numerical factors in front of the variable in a term of a polynomial or series. In the video, when simplifying the ratio of consecutive terms, the leading coefficients are what ultimately determine the limit, which is then used to apply the Ratio Test, as shown in the series with terms involving five-fourths raised to the power of N.
💡Alternating Series
An alternating series is a series where the signs of the terms alternate between positive and negative. The video script includes an example of an alternating series, and it explains how to apply the Ratio Test by considering the absolute value of the ratio, ignoring the alternating signs.
💡Simplification
Simplification in mathematics is the process of reducing an expression to a simpler form. Throughout the video, simplification is used to make the application of the Ratio Test more manageable by reducing the ratio of consecutive terms to a more straightforward expression, which is then used to determine the limit.
Highlights

The ratio test is introduced for determining the convergence of an infinite series with positive terms.

The test involves taking the limit of the absolute value of the ratio of consecutive terms of the series as it approaches infinity.

If the limit L is less than one, the series converges; if greater than one, it diverges.

The ratio test fails if the limit equals one, indicating inconclusive results for convergence or divergence.

The test is particularly useful for series involving exponentials or factorials.

An example series with exponential and factorial terms is given to demonstrate the application of the ratio test.

The simplification process for the ratio test is explained, converting terms into a product of two fractions.

The simplification leads to a fixed numerator and an increasing denominator, resulting in a limit of zero, indicating convergence.

A second example series with terms involving powers of five-fourths is analyzed using the ratio test.

The limit of the ratio for the second example is found to be greater than one, indicating divergence.

An alternating series is examined, with the absolute value of the ratio considered for the test.

The third example series involves terms with powers of two and three, demonstrating the ratio test's application to more complex terms.

The simplification of the third example results in a limit of zero, confirming the series' convergence.

The importance of the ratio test in determining the convergence of series with specific types of terms is emphasized.

The video concludes with a summary of the ratio test's outcomes based on the limit's value in relation to one.

Transcripts

Browse More Related Video

Ratio Test

Using the Ratio Test to Determine if a Series Converges #1

The Root Test

Direct comparison test | Series | AP Calculus BC | Khan Academy

Series Tests - The Ratio Test

Calculus Chapter 5 Lecture 52 Convergence Tests 2

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Ratio TestSeries ConvergenceInfinite SeriesMathematics TutorialExponential FunctionsFactorialsLimit CalculationDivergent SeriesConvergent SeriesEducational ContentMath Analysis