Ch. 13.2 Finding Limits Algebraically
TLDRIn this lesson, we explore finding limits algebraically rather than through graphical or numerical methods. We start by discussing the concept of continuity in functions and identify common continuous functions like polynomials and exponential functions. We then delve into algebraic techniques to handle discontinuities, such as factoring and rationalizing the numerator. Through detailed examples, we demonstrate how to find limits of various functions and use limit properties to simplify calculations. This foundational understanding paves the way for more advanced calculus methods.
Takeaways
- 📚 The video discusses finding limits algebraically, which involves using mathematical methods instead of graphing or numerical methods.
- 🔍 Algebraic methods for finding limits are not always applicable; sometimes numerical methods or graphing are necessary, especially when the function is not continuous at the point of interest.
- 📈 Continuity is a key concept; a continuous function can be drawn without lifting the pen from the paper, indicating no breaks, jumps, gaps, or holes.
- 🔢 If a function is continuous at a point, the limit as x approaches that point is simply the function's value at that point.
- 📉 Common continuous functions include polynomials, power functions, exponential functions, lines, cosine, and sine functions.
- 🚫 Functions that are not generally continuous include natural logarithms and tangent functions, which may have discontinuities.
- 🔧 When a function is not continuous at a certain point, algebraic manipulation can help, such as rationalizing the numerator or simplifying expressions.
- 📝 The script provides an example of simplifying a rational function by canceling out common factors to find the limit at a point where the function is not continuous.
- ✅ The properties of limits are outlined, including the ability to distribute limits over addition and subtraction, factor out constants, and evaluate limits of continuous functions by substitution.
- 📉 The video demonstrates using limit properties to evaluate a polynomial function, showing that the limit can be found by breaking down the function into simpler parts and applying the properties of limits.
Q & A
What is the main topic of the video script?
-The main topic of the video script is finding limits algebraically in calculus, using algebraic methods to analyze functions and determine limits without graphing or using numerical methods.
What is the layman's definition of a continuous function according to the script?
-The layman's definition of a continuous function is a function that can be drawn on a graph without ever lifting your pencil off the paper, implying no breaks, jumps, gaps, or holes.
Why is it useful to know if a function is continuous at a certain point when finding limits?
-If a function is continuous at a point, finding the limit as x approaches that point is straightforward because the limit is simply the function's value at that point, making the process more efficient.
Which common types of functions are always continuous according to the script?
-Common types of functions that are always continuous include polynomials, power functions, exponential functions, lines, cosine, and sine functions.
What is a technique used to deal with discontinuities in a function when finding limits?
-One technique used to deal with discontinuities is to manipulate the function using algebra, such as factoring, rationalizing the numerator, or simplifying the rational expression.
How does the script illustrate the process of finding the limit of a rational function as x approaches -1?
-The script illustrates this by factoring the rational function, canceling out terms that cause discontinuity, and then plugging in the value x = -1 to find the limit.
What is the result of the example where the script finds the limit of a rational function as x approaches 5?
-The result of the example is that the limit as x approaches 5 of the given rational function is 21/8, which is slightly more than 2.
Why is rationalizing the numerator a useful technique when finding limits?
-Rationalizing the numerator is useful when the function has a radical in the denominator that could cause discontinuity, as it helps to eliminate the problematic denominator and simplify the function for limit evaluation.
What are some of the properties of limits discussed in the script?
-Some properties of limits discussed in the script include the ability to distribute limits across addition or subtraction, factor out constants, multiply or divide limits, raise limits to a power, and evaluate limits of continuous functions by substitution.
How does the script use limit properties to evaluate the limit of a polynomial as x approaches 1?
-The script breaks down the polynomial into individual terms, applies the limit properties to separate the terms and constants, and then evaluates the limit by substituting x with 1.
Outlines
📚 Introduction to Algebraic Limit Finding
This paragraph introduces the concept of finding limits algebraically, emphasizing the use of mathematical methods instead of graphical or numerical approaches. It explains that while algebraic methods are effective for many problems, there are instances where other methods are necessary. The paragraph also introduces the concept of continuity, describing a continuous function as one that can be drawn without lifting the pencil from the paper, and notes that continuity at a point implies the limit at that point is the function's value at that point. Common continuous functions such as polynomials, power functions, exponential functions, and trigonometric functions are mentioned, with the caveat that not all functions are continuous.
🔍 Analyzing Discontinuities and Algebraic Manipulation
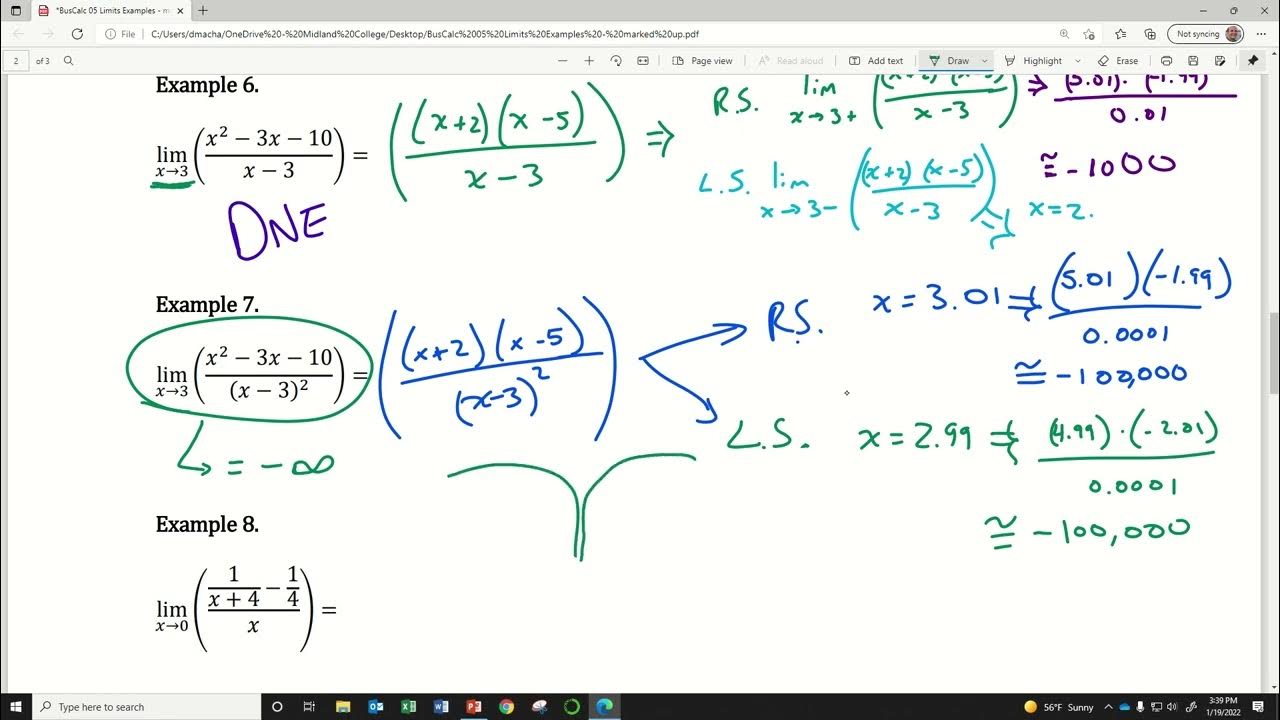
The second paragraph delves into how to handle discontinuities in functions when finding limits algebraically. It discusses the process of factoring to identify points of discontinuity, such as holes or vertical asymptotes, and the importance of being aware of these when evaluating limits. The paragraph provides an example of a rational function and demonstrates how to simplify it by canceling out common factors to find the limit as x approaches a certain value. It also touches on the idea that even if a function is not continuous at a point, the left and right-hand limits can still agree, indicating the existence of the limit.
📉 Rationalizing Numerators and Limit Properties
This paragraph focuses on the technique of rationalizing the numerator to deal with problematic denominators when finding limits. It illustrates this with an example involving a square root in the denominator, showing how to multiply by the conjugate to eliminate the square root and simplify the expression. The paragraph then transitions to discussing various properties of limits, such as the ability to distribute limits over addition and subtraction, factor out constants, and handle products, quotients, and powers. It also covers the limit of a constant and the behavior of continuous functions like polynomials and power functions when approaching a certain value.
📝 Applying Limit Properties to Polynomial Functions
The final paragraph provides an example of applying the properties of limits to evaluate the limit of a polynomial function as x approaches a specific value. Instead of directly substituting the value into the polynomial, the paragraph breaks down the polynomial into its constituent terms and applies the limit properties to each term individually. This method reinforces the understanding of why polynomials are continuous and how their limits can be evaluated by simply substituting the value of x. The paragraph concludes by showing the result of this process, which aligns with the expected outcome of directly substituting the value into the polynomial.
Mindmap
Keywords
💡Limits
💡Algebraic Methods
💡Continuity
💡Polynomials
💡Power Functions
💡Exponential Functions
💡Rational Functions
💡Rationalizing
💡Limit Properties
💡Numerical Methods
💡Factoring
Highlights
Introduction to algebraic methods for finding limits in calculus instead of numerical or graphical methods.
Explanation of when algebraic methods may not work and the necessity of numerical methods or graph analysis.
Definition and characteristics of a continuous function using both layman's and rigorous terms.
The importance of continuity in finding limits: if a function is continuous at a point, the limit is simply the function value at that point.
Identification of common continuous functions such as polynomials, power functions, exponential functions, and trigonometric functions.
Techniques for dealing with discontinuities in functions, including algebraic manipulation and rationalization.
Example of simplifying a rational function to find the limit when the point of interest causes a hole in the function.
Demonstration of how to handle limits at points of discontinuity by canceling out factors common to both numerator and denominator.
Clarification on the existence of a limit even when a function is not continuous at a specific point, as long as left and right-hand limits agree.
Procedure for finding the limit of a function as x approaches a value where the function is continuous, by direct substitution.
Use of rationalizing the numerator to handle limits involving square roots in the denominator.
Illustration of limit properties, such as the sum, difference, product, and ratio of functions, and their limits.
Application of limit properties to evaluate complex expressions by breaking them down into simpler components.
Explanation of how to handle limits of functions raised to a power using the properties of limits.
Demonstration of evaluating the limit of a polynomial using the properties of limits, showcasing the reason behind direct substitution in continuous functions.
Overview of the properties of limits for constants, continuous functions, and their implications in limit evaluation.
Final summary of the algebraic methods for finding limits and their practical applications in calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: