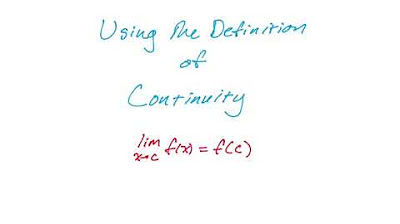Calculus AB Homework 1.3 Evaluating Limits

Michelle Krummel

19 Aug 201733:20

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial guides viewers through solving a series of calculus limit problems, from basic substitution to more complex algebraic manipulations. It covers a range of scenarios, including continuous functions, indeterminate forms, and piecewise functions. The instructor demonstrates various techniques, such as factoring and using conjugates, to find limits and emphasizes the importance of understanding the function's behavior around the point of interest. The video also explores the limits of composite functions and piecewise functions, providing insights into their continuity and existence of limits.

Takeaways

📚 The video covers a range of limit problems from a homework assignment, specifically problems 9 through 26.
🔍 For problem 9, the limit is evaluated by direct substitution, yielding a result of 20 as X approaches 5.
📈 In problem 10, the natural logarithm function's continuity at X=e is used to find the limit, which simplifies to 1/2e.
📉 Problem 11 involves the tangent function, and the limit is found by substitution, resulting in a negative value based on the reference angle in quadrant 4.
🚫 For problem 12, direct substitution results in an indeterminate form, necessitating an algebraic approach to find the limit as X approaches -2, which is -5/2.
🔄 Problem 13 showcases the use of substitution and algebraic manipulation to find the limit as theta approaches π, resulting in -2.
🌐 In problem 14, the limit of a trigonometric function as X approaches 3 is found by simplifying the expression to reveal the limit does not exist, tending towards infinity.
🔢 Problem 15 involves a difference of cubes, and the limit is found by simplifying the expression and using substitution, resulting in a limit of 27 as X approaches 3/2.
🛑 Problem 16 requires the use of the conjugate to simplify an indeterminate form, leading to a limit of 1 as X approaches -2.
➗ Problem 17 involves a complex rational expression, and after simplification, the limit as X approaches 1 is found to be -2 by canceling out a removable discontinuity.
🔄 Problem 18 deals with a complex fraction, and after simplification, the limit as X approaches 0 is determined to be positive infinity.

Q & A

What is the limit of the function 2/(5x^2) + 2 as x approaches 5 from the left-hand side?
-The limit is evaluated by substitution, resulting in (2/5) * 5^2 + 2 * 5, which simplifies to 25 + 10 or 35.
How does the limit of the natural log of x over 2x change as x approaches e?
-By substituting e for x, the natural log of e over 2e simplifies to 1/2e, since the natural log of e equals 1.
What is the approach to finding the limit of tan(alpha)/(alpha^2) as alpha approaches 5π/3?
-The substitution method is used, and since 5π/3 is in the fourth quadrant where tangent is negative, the reference angle is π/3, resulting in a limit of -√3/(25π^2/9), which simplifies to -9√3/25π^2.
Why can't the limit of x^2 - x - 6 / (2x + 4) be found by direct substitution when x approaches -2?
-Direct substitution results in 0/0, an indeterminate form, indicating that a different approach, such as factoring, is needed to find the limit.
What is the limit of the function (x + 5) / (x^2 - 9) as x approaches 3?
-The limit does not exist as the function approaches infinity, as indicated by the substitution of 3 into the function resulting in 8/0.
How is the limit of (8x^3 - 27) / (2x - 3) simplified to find the limit as x approaches 3/2?
-By factoring and canceling the common term (2x - 3), the limit is found by substitution to be 27, as the function becomes continuous at x = 3/2.
What is the limit of the square root of (2x + 5) - 1 / (x + 2) as x approaches -2?
-The limit is found by multiplying the numerator and denominator by the conjugate of the numerator, resulting in a limit of 1 as x approaches -2.
What is the approach to finding the limit of (1 - √(2x^2 - 1)) / (x - 1) as x approaches 1?
-The limit is found by multiplying the numerator and denominator by the conjugate of the numerator, simplifying to -2 as x approaches 1.
Why does the limit of the complex fraction as x approaches 0 not exist?
-The limit does not exist because the simplified form of the complex fraction results in a nonzero finite number in the numerator divided by zero, leading to positive infinity.
How does the limit of 3x + 1 / (x - 2) change as x approaches 2 from the right?
-The limit approaches infinity as x approaches 2 from the right, due to the positive values in the numerator and denominator resulting in an indeterminate form of 7/0.
What is the limit of x + sin(2x) / x as x approaches 0?
-The limit is found by splitting the fraction and using the fact that the limit of sin(kx)/x as x approaches 0 is 1, resulting in a limit of 1 + 2 * 1, which is 3.
How is the limit of sin(5x) / sin(6x) simplified as x approaches 0?
-The limit is simplified by multiplying the numerator and denominator by the respective values to make the limit of sin(kx)/kx as x approaches 0, resulting in a limit of 5/6.
Given the limit of F(x) as x approaches 4 is -7 and the limit of G(x) as x approaches 4 is 2, what is the limit of F(x) + 2 as x approaches 4?
-The limit of F(x) + 2 as x approaches 4 is found by adding the given limits, resulting in -7 + 2, which is -5.
For the piecewise function defined as 3 - x for x < 2 and x / (2 + 1) for x > 2, at what point C does the limit exist?
-The limit exists for all values of x except when x is equal to 2, as the left-hand and right-hand limits at x = 2 are not equal, resulting in a non-existent two-sided limit at x = 2.
For the piecewise function defined as 1 - x^2 for x ≠ -1 and 2 for x = -1, at what point C does the limit exist?
-The limit exists for all real numbers, as the left-hand and right-hand limits at x = -1 are equal, and the function is continuous everywhere else on its domain.

Outlines

00:00

📚 Calculus Homework Solutions

This paragraph discusses the process of solving calculus homework problems, specifically focusing on limits. The speaker walks through various problems, starting with a limit involving a continuous function at x=5, using substitution to find the solution. The explanation continues with limits involving natural logarithms, tangent functions, and rational functions, highlighting the use of algebraic manipulation and substitution where applicable. The paragraph emphasizes the importance of recognizing indeterminate forms and the need for alternative methods when direct substitution fails.

05:02

🔍 Advanced Limit Evaluation Techniques

The speaker delves into more complex limit problems, employing algebraic simplification and factoring to address indeterminate forms such as 0/0. The paragraph covers the use of conjugates to simplify expressions and the concept of removable discontinuities. It provides step-by-step solutions for limits involving square roots and polynomial functions, demonstrating how to transform the expressions to find determinate limits, even in cases where direct substitution results in an indeterminate form.

10:06

📉 Limits of Trigonometric Functions and Complex Fractions

This section of the script addresses the limits of trigonometric functions, particularly focusing on the behavior of sine functions as they approach specific values. The speaker explains how to simplify complex fractions by finding a common denominator and emphasizes the importance of not prematurely concluding the limit's value. The paragraph also touches on the behavior of limits as they approach infinity and how to determine whether a limit exists by evaluating from both the left and right-hand sides.

15:08

🔢 Limits Involving Piecewise Functions and Special Cases

The speaker tackles limits involving piecewise functions, explaining how to evaluate them by considering each segment's continuity and the behavior at specific points. The paragraph discusses how to find two-sided limits and determine the existence of a limit at a point where the function is not defined. It also covers the concept of limits involving the sum, difference, and product of functions, providing examples of how to apply given limits to find new limits.

20:14

📌 Limit Existence in Piecewise Functions

This paragraph examines the existence of limits in piecewise functions, focusing on the continuity and the behavior as x approaches certain values. The speaker explains how to determine the left and right-hand limits and how their equality is crucial for the existence of a limit. The paragraph provides examples of evaluating limits at points of discontinuity and demonstrates the process of finding the set of points for which the limit exists, using both interval and set notation.

25:14

📘 Comprehensive Limit Analysis for Piecewise Functions

The final paragraph provides a detailed analysis of limits for piecewise functions, emphasizing the need to evaluate limits from both directions at points of discontinuity. The speaker discusses the continuity of each piece of the function and the process of finding left and right-hand limits. The paragraph concludes with the determination of the set of all real numbers for which the limit exists, using interval notation to represent the range of x values.

Mindmap

Keywords

💡Limit

In the context of the video, 'limit' refers to the value that a function or sequence approaches as the input (often denoted as 'x') approaches a certain value (denoted as 'c'). The concept is central to calculus and is used to understand the behavior of functions at specific points or as they extend to infinity. The script discusses various limits, such as 'the limit as X approaches 5 from the left-hand side', to illustrate different scenarios where the function may or may not be continuous.

💡Continuous

A function is 'continuous' at a point if the limit of the function as x approaches that point is equal to the function's value at that point. Continuity is a fundamental concept in calculus, indicating that there are no abrupt changes in the function's value. The script mentions 'continuous' when discussing the properties of functions at certain points, such as 'X is continuous at 5', indicating that the function's value at X=5 matches the limit as X approaches 5.

💡Substitution

In mathematics, 'substitution' is a method where a value is directly inserted into an expression to evaluate it. In the context of limits, substitution is often used when the function is continuous at a point to find the limit by simply replacing the variable with the point of interest. The script uses 'substitution' in multiple examples, such as 'we simply substitute 5 in for X', to demonstrate how to calculate limits for continuous functions.

💡Indeterminate Form

An 'indeterminate form' arises when an expression results in a form like 0/0 or ∞/∞, which does not provide enough information to determine the limit's value. The script mentions 'indeterminate form' in cases where direct substitution results in such a form, indicating that alternative methods must be used to evaluate the limit, as seen in 'zero over zero is indeterminate'.

💡Algebraic Approach

An 'algebraic approach' involves manipulating the algebraic expression of a function to simplify it or to put it in a form that makes it easier to evaluate limits. The script refers to using an 'algebraic approach' when direct substitution is not helpful, such as in 'let's try using an algebraic approach instead we can factor the numerator', to show how to deal with indeterminate forms or discontinuities.

💡Removable Discontinuity

A 'removable discontinuity' occurs at a point where the function is not defined or the limit exists but is not equal to the function's value at that point, yet the discontinuity can be 'removed' by algebraic manipulation, such as canceling out a common factor. The script discusses 'removable discontinuity' in the context of simplifying expressions to make them continuous at certain points, as in 'this is a removable discontinuity and when I cancel out that common factor'.

💡Piecewise Function

A 'piecewise function' is a function defined by multiple pieces, each with its own expression, typically applied over different intervals of the domain. The script mentions 'piecewise function' when discussing functions defined by different rules for different ranges of X, such as 'we have a piecewise function and it's defined as 3 - X when X is less than 2', to illustrate how to find limits at points where the function definition changes.

💡Left-Hand Limit

The 'left-hand limit' is the limit of a function as the input approaches a certain value from the left side, indicating numbers slightly less than the point of interest. The script uses 'left-hand limit' to describe the behavior of functions as they approach a point from the left, as in 'the limit of f of X as X approaches 2 from the left-hand side'.

💡Right-Hand Limit

The 'right-hand limit' is similar to the left-hand limit but approaches the value from the right side, indicating numbers slightly greater than the point of interest. The script discusses 'right-hand limit' to determine the behavior of functions as they approach a point from the right, such as 'the limit of f of X as X approaches 2 from the right-hand side'.

💡Trigonometric Functions

Trigonometric functions, such as sine and cosine, are mathematical functions of an angle, widely used in various fields including calculus. The script refers to 'trigonometric functions' in the context of evaluating limits involving these functions, such as 'sine of PI over 3', to demonstrate their role in solving limit problems.

Highlights

The limit of a function as X approaches a certain value can be evaluated using substitution if the function is continuous at that point.

For functions that are not continuous at a point, an indeterminate form like 0/0 may require algebraic manipulation to find the limit.

The natural logarithm of 'e' over 2 times 'e' simplifies to 1, demonstrating a straightforward limit calculation.

Tangent function's limit at a specific angle can be found using reference angles and trigonometric identities.

When a rational function is not defined at a certain point, the limit may involve a removable discontinuity, requiring factorization.

The limit of a function as X approaches infinity or negative infinity can be determined by the behavior of the function's leading terms.

For complex fractions, finding a common denominator can simplify the expression and help in evaluating the limit.

Multiplying by the conjugate of a numerator can be a technique to simplify an expression with a square root in the denominator.

The limit of a function at a point can be influenced by the behavior of the function as it approaches that point from both sides.

The limit of a function at a point where the function is not defined can be evaluated by approaching that point from the left and right.

The limit of a sum or difference of functions as X approaches a value can be found by using the individual limits of those functions.

The limit of a product or quotient of functions can be evaluated by considering the limits of the individual functions and their operations.

The limit of a function raised to a power can be found by squaring the limit of the function, if applicable.

The existence of a limit for a piecewise function depends on the continuity and limit behavior of each piece of the function.

A piecewise function's limit at a point of transition can be evaluated by considering the left and right limits separately.

The limit of a function at a point where the function is defined by different expressions can be found by direct substitution, if continuous.

For piecewise functions, the overall limit behavior can be described using interval notation or set notation to indicate where the limit exists.

Transcripts

Browse More Related Video

AP Calculus AB - 1.5 Determining Limits Using Algebraic Properties of Limits

Computing Multivariable Limits Algebraically

Using the Definition of Continuity in Calculus

Calculus AB Homework 4.3: L'Hospital's Rule

Calculus AB - Unit 1 Review

Calculus Math 133 Worksheet 1

Related Tags

Calculus Limits Homework Trigonometry Algebra Continuous Functions Indeterminate Forms Piecewise Functions Substitution Method Limit Existence