Ch. 11.4 Shifted Conics
TLDRThis script delves into the concept of shifted conics, akin to shifting functions in algebra, but without stretching or compressing. The focus is on translating conic sections—ellipses, hyperbolas, and parabolas—vertically and horizontally, and deriving new equations based on these movements. The instructor emphasizes the importance of identifying the new center of the conic and understanding how it affects the axes of symmetry. Through an example, the process of shifting an ellipse is demonstrated, including adjusting the major and minor axes, vertices, and foci. The script concludes with the general equation for any conic section and how it can be manipulated to identify the type of conic, whether it's a parabola, ellipse, hyperbola, or a special case like a circle.
Takeaways
- 📚 The lesson focuses on shifted conics, which is similar to shifting functions but without altering their stretch or compression.
- 🔄 Shifting a conic involves moving it up, down, left, or right, and the new center affects the axes of symmetry and orientation of the major and minor axes.
- 📏 Understanding the new center of the conic is crucial for determining the positions of the vertices, foci, and axes after the shift.
- 📐 The general equation for any conic section is presented, with the form: "Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0", where coefficients determine the type of conic.
- 🔍 Completing the square for both x and y in the general equation can transform it into the specific forms of ellipses, hyperbolas, or parabolas.
- 📈 The presence of "x^2" or "y^2" terms indicates a parabola, while both terms with the same sign suggest an ellipse, and identical coefficients result in a circle.
- 🔺 The absence of "x^2" or "y^2" terms and the presence of a linear term can indicate a degenerate conic, which simplifies to a line, point, or no solution.
- 📉 The orientation of the major axis (along x or y) changes with the shift and determines where the vertices of the conic are located.
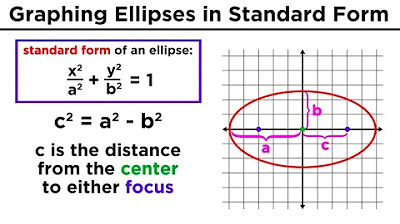
- 📍 The foci of the conic can be found using the relationship "c^2 = a^2 - b^2", with c representing the distance from the center to each focus.
- 📘 The script provides an example of shifting an ellipse, demonstrating how to calculate new vertices and foci based on the shift.
- 🖋️ The process of shifting conics involves understanding the original conic's properties and applying geometric transformations to find the new positions.
Q & A
What is the main topic of the lecture in the provided transcript?
-The main topic of the lecture is shifted conics, focusing on how to move conic sections up, down, left, and right, and how to find the equations based on those shifts.
Why is the center of a conic important when discussing shifts?
-The center of a conic is important because it determines the location of the axes of symmetry, the major and minor axes, and the transverse axis. Once the conic is shifted, everything is related to the new center.
What happens to the axes of a conic when it is shifted?
-When a conic is shifted, the axes of symmetry, including the major and minor axes or the transverse axis, change their positions relative to the new center of the conic.
How does the lecturer determine the vertices of a shifted ellipse?
-The lecturer determines the vertices of a shifted ellipse by understanding the new center's position and then applying the lengths of the major and minor axes from that center, adjusting for the shift.
What is the significance of the equation 'c squared equals a squared minus b squared' in the context of conics?
-This equation is used to find the distance 'c' from the center of a conic to its foci. It is derived from the Pythagorean theorem and is essential for determining the location of the foci after a conic has been shifted.
How does the lecturer describe the process of finding the foci of a shifted ellipse?
-The lecturer describes finding the foci by first calculating the value of 'c' using the equation 'c squared equals a squared minus b squared', and then applying this distance to the y-values of the new center since the major axis runs vertically.
What is the general equation for any conic section, according to the transcript?
-The general equation for any conic section is given by the formula that includes terms for x squared, y squared, x, y, and a constant, along with a mixed term. It can represent various types of conics depending on the coefficients.
How can the general equation of a conic be transformed into the specific form of an ellipse, hyperbola, or parabola?
-The general equation can be transformed into the specific form of an ellipse, hyperbola, or parabola by completing the square for x and y, which manipulates the coefficients a, b, c, d, e, and f into the standard forms of these conics.
What does the transcript suggest about the conditions for a conic to be a parabola?
-The transcript suggests that for a conic to be a parabola, either the x squared term or the y squared term must be non-zero while the other is zero, indicating only one squared term is present in the equation.
How can you determine if a conic is an ellipse or a hyperbola based on the coefficients a and c?
-If both a and c are non-zero and have the same sign, the conic is an ellipse. If one is positive and the other is negative, the conic is a hyperbola. If a and c are identical, the conic is a circle.
What is the term used to describe a conic that degenerates into a first-degree equation?
-A conic that degenerates into a first-degree equation, such as a line or a point, is referred to as 'degenerative'.
Outlines
📚 Introduction to Shifted Conics
This paragraph introduces the concept of shifted conics, drawing parallels to how functions are shifted in previous chapters. The focus is on the translation of conic sections—ellipses, hyperbolas, and parabolas—along the axes, rather than transformations like stretching or compressing. The importance of recognizing the new center of the conic after shifting is emphasized, as it determines the location of the axes of symmetry. An example of an ellipse is used to illustrate the process of shifting and how to determine the new vertices and foci based on the new center.
📐 Shifting Conics: Axes and Foci Calculation
The second paragraph delves deeper into the mechanics of shifting conics, using the example of an ellipse to explain how to calculate the new positions of the axes and foci after a conic has been translated. It discusses the process of finding the new center and using it to determine the vertices of the major and minor axes, as well as the foci. The paragraph highlights the method of applying shifts to the y-values for the major axis and x-values for the minor axis, and the use of the Pythagorean theorem to find the distance 'c' from the center to the foci. It also suggests the utility of graphing to visualize these transformations.
📘 General Equation of Conic Sections
The final paragraph presents the general equation for any conic section, which applies regardless of whether the conic has been shifted, rotated, or transformed in any way. It explains that the presence and coefficients of terms in the equation determine the type of conic section—whether it's a parabola, ellipse, hyperbola, or a special case like a circle. The paragraph also touches on the concept of degenerate conics, which occur when the equation simplifies to a line, point, or no solution at all. It concludes with a guide on how to identify the type of conic based on the signs and values of coefficients 'a' and 'c'.
Mindmap
Keywords
💡Shifted Conics
💡Center
💡Major Axis
💡Minor Axis
💡Equation of a Conic
💡Vertices
💡Foci
💡Directrix
💡Completing the Square
💡General Form of a Conic
💡Degenerative Conic
Highlights
Introduction to shifted conics, comparing the process to shifting functions in Chapter 2 but without stretching or compressing.
Focus on the center of conics and how shifts affect the axes of symmetry and the major and minor axes.
Explanation of deriving equations for conics based on shifts, emphasizing the importance of the new center.
Example of shifting an ellipse, detailing the process of moving the center and adjusting the axes.
Understanding the new positions of the major and minor axes after a conic has been shifted.
Calculating the vertices of the shifted ellipse, including adjustments for the major and minor axes.
Determining the new foci of the ellipse using the relationship c^2 = a^2 - b^2.
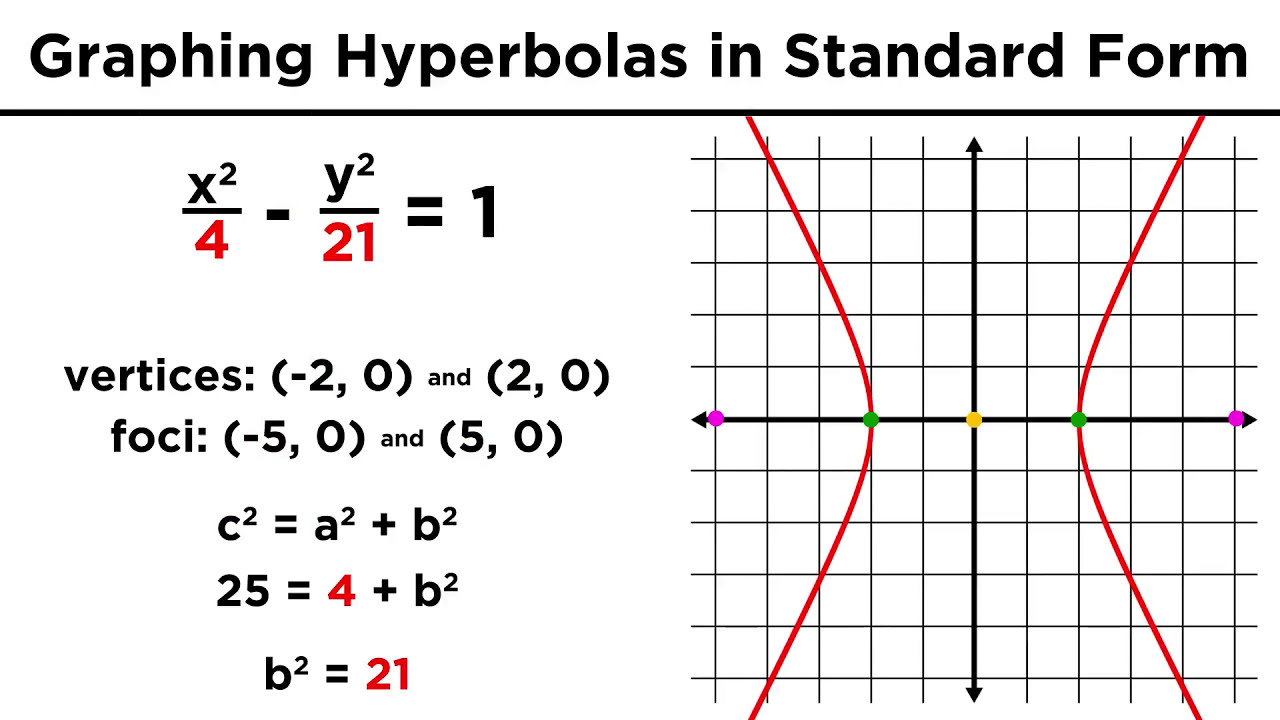
Illustration of how to apply shifts to other conic sections like hyperbolas and parabolas.
The general equation for any conic section, including the significance of coefficients a, b, c, d, e, and f.
Transformation of the general conic equation into specific forms for ellipses, hyperbolas, and parabolas.
The concept of degenerative conics, where the general equation simplifies to a line, point, or no solution.
Identification of conic types based on the coefficients a and c, including parabolas, ellipses, circles, and hyperbolas.
Clarification on the interpretation of 'a or c is non-zero' in the context of identifying parabolas.
The necessity of both x^2 and y^2 terms for an ellipse and the condition for a circle.
Differentiation between an ellipse and a hyperbola based on the signs of coefficients a and c.
The importance of visualizing conic sections through graph drawing to aid in understanding shifts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: