Calculus 1 - Introduction to Limits
TLDRThis video script offers a comprehensive introduction to limits, detailing both analytical and graphical methods for evaluation. It illustrates how to handle undefined expressions by substituting values close to the limit point and demonstrates techniques such as factoring and using conjugates for complex fractions and square roots. The script also explains one-sided limits and how to identify different types of discontinuities, such as jumps and holes, providing clear examples and encouraging viewers to solve problems interactively.
Takeaways
- 📚 Introduction to limits: The video begins with a basic introduction to limits, explaining how to evaluate them both analytically and graphically.
- 🔢 Direct Substitution: The method of direct substitution is explained, where you plug in the value of x into the function to find the limit, unless it results in an undefined form like 0/0.
- 🔍 Approaching Values: When direct substitution leads to an undefined form, the technique of plugging in values close to but not equal to the limit value is suggested.
- 📈 Factoring to Simplify: The video demonstrates how factoring can help simplify expressions to find limits, especially when dealing with undefined forms like 0/0.
- 🤔 Alternative Techniques: It is acknowledged that sometimes other techniques are necessary to find limits, and examples of such techniques are provided throughout the video.
- 📊 Evaluating Polynomial Functions: The process of evaluating limits for polynomial functions is shown, where direct substitution is typically possible without issues.
- 🛑 Complex Fractions: For complex fractions, the video recommends multiplying the numerator and denominator by the common denominator to simplify the expression.
- 🌐 Factoring Differences of Cubes: Specific to expressions like x^3 - 27, the video explains how to factor using the difference of cubes formula.
- 🔄 Canceling Factors: The importance of canceling out common factors in the numerator and denominator to simplify the limit expression is emphasized.
- 📉 One-Sided Limits: The concept of one-sided limits is introduced, explaining how to evaluate the limit as x approaches a value from the left and from the right, and how these can differ.
- 📊 Graphical Evaluation: The video concludes with a section on evaluating limits graphically, showing how to interpret a graph to find the y-values corresponding to the limit from different approaches.
Q & A
What is the basic concept of limits in calculus?
-The basic concept of limits in calculus refers to the value that a function approaches as the input (x-value) gets arbitrarily close to a certain point. It is a fundamental idea used to define the continuity of functions, derivatives, and integrals.
What are the two primary ways to evaluate limits mentioned in the transcript?
-The two primary ways to evaluate limits mentioned in the transcript are analytically, which involves algebraic manipulation of the function to find the limit, and graphically, which involves observing the function's graph to determine the limit's value as x approaches a certain point.
Why can't we directly substitute the value of x when it results in a 'zero over zero' situation?
-We cannot directly substitute the value of x in a 'zero over zero' situation because it results in an undefined expression. To find the limit in such cases, we often need to simplify the expression by factoring or using other algebraic techniques to eliminate the indeterminate form.
How does the process of factoring help in evaluating limits?
-Factoring helps in evaluating limits by simplifying the expression, particularly when dealing with fractions that have a 'zero over zero' indeterminate form. By factoring, we can cancel out common factors in the numerator and denominator, which may reveal a simpler limit expression that can be evaluated directly.
What is the difference between a removable and a non-removable discontinuity?
-A removable discontinuity, also known as a hole, occurs when the function is undefined at a point but the limit from both sides exists and is the same. By redefining the function at that point, the discontinuity can be removed. A non-removable discontinuity, such as a jump or an infinite discontinuity, occurs when the limit does not exist or the left-sided and right-sided limits are different, indicating the function has a true break at that point.
How can you determine the left-sided and right-sided limits graphically?
-To determine the left-sided limit graphically, you approach the vertical line corresponding to the point of interest from the left side of the graph and observe the y-value the function approaches. For the right-sided limit, you do the same but from the right side. If the left-sided and right-sided limits are not the same, the overall limit does not exist.
What is the role of the conjugate in evaluating limits involving square roots?
-When evaluating limits involving square roots, the conjugate of the expression under the square root is used to eliminate the square root in the denominator. This is done by multiplying both the numerator and the denominator by the conjugate, which simplifies the expression and often reveals a simpler limit that can be evaluated directly.
What is the significance of vertical asymptotes in the context of limits?
-Vertical asymptotes indicate points where the function approaches positive or negative infinity as x approaches a certain value. These points are significant because they represent non-removable discontinuities, and the limit does not exist at such points since the function does not approach a finite value.
How does the technique of direct substitution work in evaluating limits?
-Direct substitution works by plugging the value of x that the limit is approaching directly into the function. If the function does not result in an undefined expression, the value of the function at that point is the limit. This technique is straightforward and can be used when the denominator does not become zero when x approaches the value of interest.
What is the purpose of using one-sided limits in calculus?
-One-sided limits are used to determine the behavior of a function as it approaches a certain value from either the left or the right. They are important when the function is not continuous at that point, and the behavior from each side is different. One-sided limits help in understanding the function's behavior and in determining the points of discontinuity.
How can you evaluate the limit of a complex fraction?
-To evaluate the limit of a complex fraction, you first multiply the numerator and the denominator by the common denominator to simplify the expression. If the fraction involves radicals, you also multiply by the conjugate of the radical expression to eliminate the square roots in the denominator. After simplification, you can use direct substitution to find the limit as x approaches the value of interest.
Outlines
📚 Introduction to Limits and Evaluation Techniques
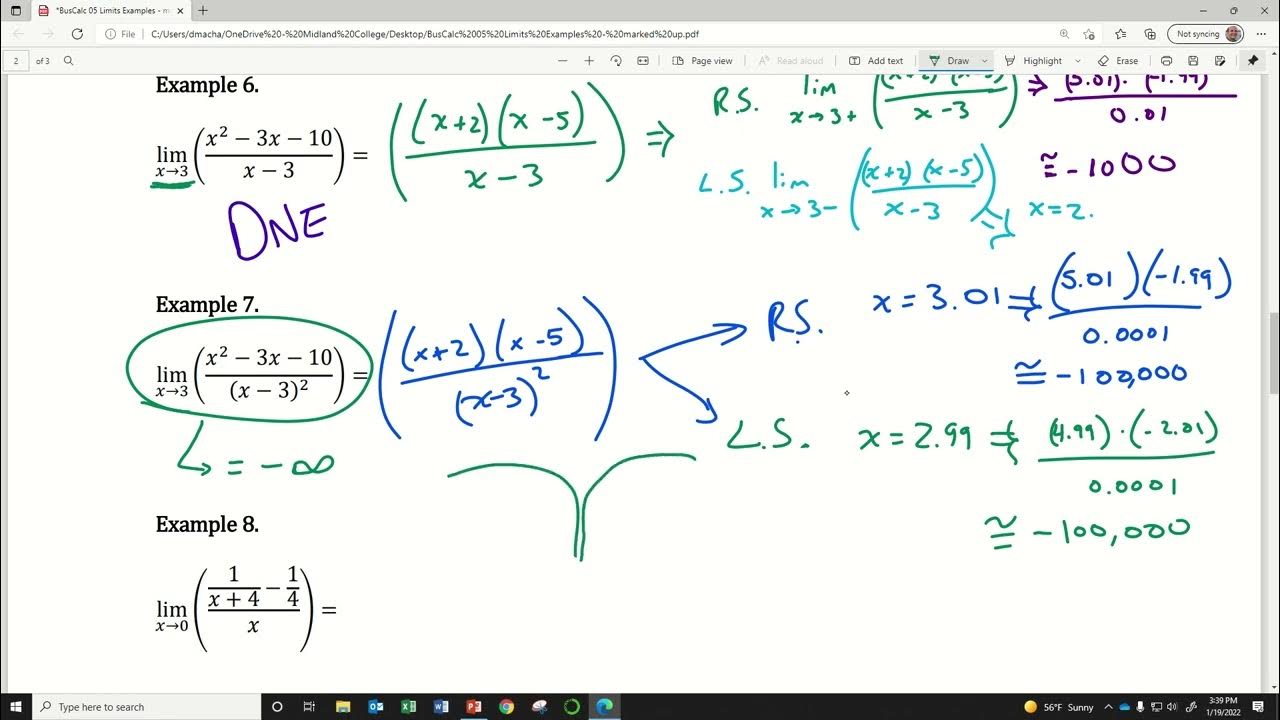
This paragraph introduces the concept of limits in calculus, explaining how to evaluate them both analytically and graphically. It begins with a simple example of finding the limit as x approaches 2 for the function (x^2 - 4) / (x - 2). The video discusses the issue of encountering an undefined value upon direct substitution and suggests alternative methods, such as substituting values close to but not equal to 2, to approximate the limit. It also covers the technique of factoring the expression to simplify the limit calculation, as demonstrated by factoring x^2 - 4 into (x + 2)(x - 2). The paragraph further explains how to handle limits with no fractions by using direct substitution, as seen in the example of x^2 + 2x - 4 when x approaches 5. Additionally, it addresses the scenario of a 0/0 indeterminate form by factoring the expression, as shown in the example of x^3 - 27 / (x - 3).
🔢 Solving Complex Fractions and Roots
This paragraph delves into techniques for evaluating limits involving complex fractions and square roots. It starts by addressing a complex fraction and suggests multiplying the numerator and denominator by the common denominator to simplify the expression. The video then demonstrates how to handle square roots by multiplying the numerator and denominator by the conjugate of the square root expression. The paragraph provides step-by-step examples of how to manipulate these expressions to cancel out the variable terms and isolate the limit. It also discusses the concept of one-sided limits and how they can differ from the limit from both sides, emphasizing the importance of checking both left and right approaches to a point.
📈 Evaluating Limits Graphically
This paragraph explains the process of evaluating limits graphically by interpreting the function's graph. It illustrates how to find the limit as x approaches a certain value by tracing the function's curve up to a vertical line at that value from both the left and right sides. The video clarifies that if the left-sided and right-sided limits match, the limit exists; otherwise, it does not. It also shows how to find the function value at a specific point by identifying the y-coordinate of the closed circle on the graph. The paragraph highlights the concepts of removable and non-removable discontinuities, such as holes and jump discontinuities, and how they affect the existence of limits.
🚫 Discontinuities and Asymptotes
This paragraph discusses the impact of discontinuities and asymptotes on the evaluation of limits. It explains that when a function has a vertical asymptote at a certain value of x, the limit does not exist as the function's value approaches infinity or negative infinity. The video provides an example of a function with a vertical asymptote at x equals 3, where the left-sided limit approaches negative infinity, and the right-sided limit approaches positive infinity. It also mentions a jump discontinuity at x equals -3, which is a non-removable discontinuity, and a hole at x equals -2, which is a removable discontinuity. The paragraph emphasizes the importance of identifying these discontinuities when working with limits.
Mindmap
Keywords
💡Limits
💡Analytical Evaluation
💡Graphical Evaluation
💡Direct Substitution
💡Factoring
💡Indeterminate Forms
💡Vertical Asymptote
💡One-Sided Limits
💡Jump Discontinuity
💡Conjugate
💡Complex Fractions
Highlights
Introduction to limits and their evaluation methods.
Analytical method of evaluating limits using direct substitution.
Graphical method of evaluating limits by observing function behavior.
Handling undefined limits with zero over zero indeterminate forms.
Using逼近 values to find limits when direct substitution is not possible.
Factoring to simplify limit expressions, especially with difference of cubes.
Direct substitution for limits when the denominator does not involve the variable.
Solving complex fractions by finding a common denominator and simplifying.
Dealing with square roots in limits by multiplying by the conjugate of the expression.
One-sided limits and their significance in determining the existence of a limit.
Identifying vertical asymptotes and their impact on limit evaluation.
Recognizing and evaluating jump discontinuities and removable discontinuities.
Practical examples of limit evaluation with step-by-step explanations.
Understanding the concept of limits for functions with radical expressions.
The role of factoring in simplifying expressions to evaluate limits analytically.
Visual representation of limits on a graph and how to interpret them.
The impact of undefined function values at certain points on limit evaluation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: