Calculus 1 Final Exam Review
TLDRThis video tutorial covers essential calculus topics such as limits, continuity, derivatives, integration, and their subtopics, catering to both college and high school students preparing for Calculus I final exams or AP Calculus exams. The instructor demonstrates problem-solving techniques, including direct substitution, factoring, power and product rules, implicit differentiation, and u-substitution. The video also addresses related rates problems, identifying intervals of increase and concavity, and evaluating limits and integrals, providing a comprehensive review for exam success.
Takeaways
- 📚 The video is a comprehensive guide for students preparing for Calculus exams, covering topics like continuity, limits, derivatives, and integration.
- 🔍 The script emphasizes the importance of recognizing when direct substitution is not applicable due to undefined expressions, such as division by zero.
- 📈 It provides a step-by-step method for factoring expressions, particularly difference of squares and trinomials, to simplify limit calculations.
- 🧮 The video explains the power rule for derivatives and how to apply it to various functions, including x to the nth power and roots of x.
- 🤔 The script illustrates how to find the value of a constant that ensures a piecewise function is continuous at a specific point by setting the function's parts equal.
- 📊 The video covers the differentiation of exponential and logarithmic functions, as well as the product rule for differentiating the product of two functions.
- 🌀 It explains the process of evaluating integrals using the power rule for integration and the concept of anti-derivatives.
- 📈 The script teaches how to find the equation of a tangent line to a curve using implicit differentiation and the point-slope formula.
- 🚰 The video addresses a real-world problem of water filling a cylinder, demonstrating the use of related rates to determine the change in volume with respect to time.
- 📈 It explains how to identify intervals where a function is increasing or decreasing by analyzing the first derivative and critical points.
- 📊 The script concludes with a method for calculating the average value of a function over a given interval, using definite integrals and the width of the interval.
Q & A
What is the main topic of the video?
-The main topic of the video is to provide a comprehensive review and guidance for students preparing for Calculus exams, covering key topics such as continuity, limits, derivatives, integration, and their subtopics.
How does the video approach the concept of limits?
-The video approaches the concept of limits by first suggesting direct substitution and then explaining the necessity of factoring expressions when direct substitution is not possible due to undefined expressions.
What is the method used to solve the first limit problem in the video?
-The method used to solve the first limit problem is factoring the expression to eliminate the undefined denominator, allowing for direct substitution to find the limit as x approaches the value that caused the initial undefined expression.
How is the power rule applied in the video?
-The power rule is applied in the video by differentiating each term of the given expression individually, using the rule that the derivative of a variable raised to a constant is the constant times the variable raised to the constant minus one.
What is the significance of the value 'c' in the context of making a piecewise function continuous?
-The significance of 'c' is that it is the value that must be found and substituted into the piecewise function to ensure that the two parts of the function are equal at the point where the function changes, thus making the entire piecewise function continuous.
How does the video explain the concept of implicit differentiation?
-The video explains implicit differentiation as a method used to find the derivative of y with respect to x in problems where the relationship between x and y is given implicitly, such as in the equation of a curve. It involves differentiating each term of the equation with respect to x and solving for dy/dx.
What is the purpose of the product rule in differentiation?
-The purpose of the product rule in differentiation is to find the derivative of a product of two functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function.
How does the video demonstrate the evaluation of an integral?
-The video demonstrates the evaluation of an integral by first simplifying the integrand, then applying the power rule for integration, which involves adding one to the exponent of the variable, and dividing by the new exponent, while also including the constant of integration.
What is the significance of the second derivative in the context of concavity?
-The significance of the second derivative in the context of concavity is that it indicates whether the function is concave up or concave down. A positive second derivative indicates concavity up, while a negative second derivative indicates concavity down.
How does the video suggest identifying intervals of increase or decrease?
-The video suggests identifying intervals of increase or decrease by first finding the first derivative of the function, setting it equal to zero to find critical points, and then testing values in the intervals defined by these critical points to determine the sign of the first derivative and thus whether the function is increasing or decreasing.
What is the method for evaluating limits of complex fractions as described in the video?
-The method for evaluating limits of complex fractions involves eliminating the smaller fractions by multiplying the numerator and the denominator by the common denominator, simplifying the resulting expression, and then applying direct substitution with the limit's value.
Outlines
📚 Calculus Exam Review: Limits, Derivatives, and Integrals
This paragraph introduces a video aimed at students preparing for Calculus exams, including College and AP Calculus tests. The video covers key topics such as continuity, limits, derivatives, integration, and subtopics within these chapters. It begins with an example of evaluating a limit using factoring and direct substitution, highlighting the importance of recognizing when direct substitution is not possible due to issues like division by zero.
🔍 Piecewise Function Continuity and Derivative Application
The second paragraph focuses on a problem involving a piecewise function and finding the value of a constant 'c' to ensure continuity. It explains that for the function to be continuous, the two parts of the piecewise function must be equal at the junction point. The video demonstrates solving for 'c' by setting the two parts equal to each other at x=3 and solving the resulting equation. The process involves simplifying and solving a linear equation for 'c', ultimately finding that c=5 ensures the function's continuity.
🧪 Differentiating Exponential and Logarithmic Functions
This paragraph delves into the differentiation of exponential and logarithmic functions, emphasizing the use of the product rule. It explains the derivative of exponential functions as e^u * u' and the derivative of natural logarithm functions as (1/u) * u'. The video provides examples of differentiating e^(x^2) and ln(x^2 + 7), showcasing the application of the product rule for the latter. The explanation includes finding the derivative of a composite function involving both exponential and logarithmic parts.
📈 Evaluating Integrals and Implicit Differentiation
The fourth paragraph discusses the evaluation of integrals and the concept of implicit differentiation. It begins with simplifying an integral expression and applying the power rule for integration. The video then moves on to finding the equation of the tangent line to a curve using implicit differentiation. It explains the process of differentiating each term with respect to x and using the point-slope formula to find the slope of the tangent line at a given point (2,3). The final step is to write the equation of the tangent line in standard form, which matches one of the multiple-choice answers provided.
🤔 Understanding Limits and Related Rates
This paragraph addresses the concept of limits, particularly focusing on the limit as a function's derivative at a point. It explains that the limit of (f(x+h) - f(x))/h as h approaches zero is equal to f'(x), the derivative of the function at x. The video provides an example where no direct calculation is possible, and the only way to find the answer is to understand the meaning behind the limit expression. It also introduces a related rates problem involving the volume of water in a cylinder, explaining how to find the rate of change of volume with respect to time using implicit differentiation.
📊 Identifying Increasing Intervals and Maximum Values
The sixth paragraph discusses the process of identifying intervals where a function is increasing by finding critical points and analyzing the first derivative. It explains that the function is increasing where the first derivative is positive and decreasing where it is negative. The video demonstrates this by finding the critical points of a given function and testing values around these points to determine the intervals of increase. It also shows how to identify the location and maximum value of a function by finding the critical point where the first derivative is zero and analyzing the sign changes of the first derivative around this point.
📈 Calculating Average Function Value
This paragraph explains the concept of calculating the average value of a function over a given interval. It introduces the formula for average value, which involves dividing the definite integral of the function over the interval by the width of the interval. The video demonstrates the process by finding the anti-derivative of the function, evaluating it at the endpoints of the interval, and then applying the average value formula. The example provided involves a cubic function, and the video concludes with the calculation of the average y-value over the interval from 1 to 5.
🔢 Evaluating Composite Functions and Limits
The eighth paragraph covers the evaluation of composite functions using the chain rule and the evaluation of limit expressions. It explains the chain rule as the derivative of the outer function times the derivative of the inner function. The video demonstrates the process by differentiating a composite function involving x to the eighth power and simplifying the result. It then moves on to evaluating a limit expression by using a calculator to approximate the limit and by simplifying the expression algebraically to find the exact limit value.
📉 Identifying Concave Downward Intervals
The final paragraph focuses on identifying intervals where a function is concave downward by examining the second derivative. It explains that a function is concave down when the second derivative is negative. The video demonstrates the process by finding the first and second derivatives of a given function, setting the second derivative to zero to find critical points, and analyzing the sign changes of the second derivative to determine the intervals of concavity. The example provided identifies the interval from negative infinity to 2 as the region where the function is concave downward.
Mindmap
Keywords
💡Calculus
💡Limits
💡Derivatives
💡Integration
💡Continuity
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Power Rule
💡Antiderivatives
💡Related Rates
Highlights
The video covers key calculus topics such as continuity, limits, derivatives, integration, and their subtopics.
The video is useful for college students preparing for their Calculus I final exam or high school students taking the AP Calculus exam.
When direct substitution in limits is not possible, factoring the expression can help find the limit.
The difference of perfect squares can be factored using the square root of the terms involved.
The video demonstrates how to evaluate limits by factoring and simplifying expressions.
Understanding the power rule is essential for differentiating functions raised to a constant.
The power rule for derivatives states that the derivative of x to the n is n times x to the n minus one.
The video provides a method for finding the value of a constant that makes a piecewise function continuous.
To ensure a piecewise function is continuous, the function values at the point of discontinuity must be equal.
The video explains how to differentiate exponential and logarithmic functions using their respective rules.
The product rule is introduced for differentiating the product of two functions, with examples provided.
The video walks through the process of evaluating integrals using the power rule for integration.
The power rule for integration involves adding one to the exponent and dividing by the result.
The video demonstrates how to find the equation of the tangent line to a curve using implicit differentiation.
To find the tangent line's slope, the video shows how to differentiate the curve's equation with respect to x.
The point-slope form of the tangent line equation is derived and then converted to standard form.
The video addresses a limit problem by explaining the concept of f prime of x and how it relates to the derivative of a function.
A method for evaluating limits using a calculator is discussed, showing how to approximate the limit by plugging in values close to the point of interest.
The video concludes with a problem on identifying intervals of concavity, focusing on the second derivative's role in determining concavity.
The second derivative being negative indicates the function is concave downward, while a positive second derivative means the function is concave upward.
The video provides a comprehensive overview of calculus concepts, offering practical examples and problem-solving techniques for students at different levels.
Transcripts
Browse More Related Video

What We Must Know for Calculus AB
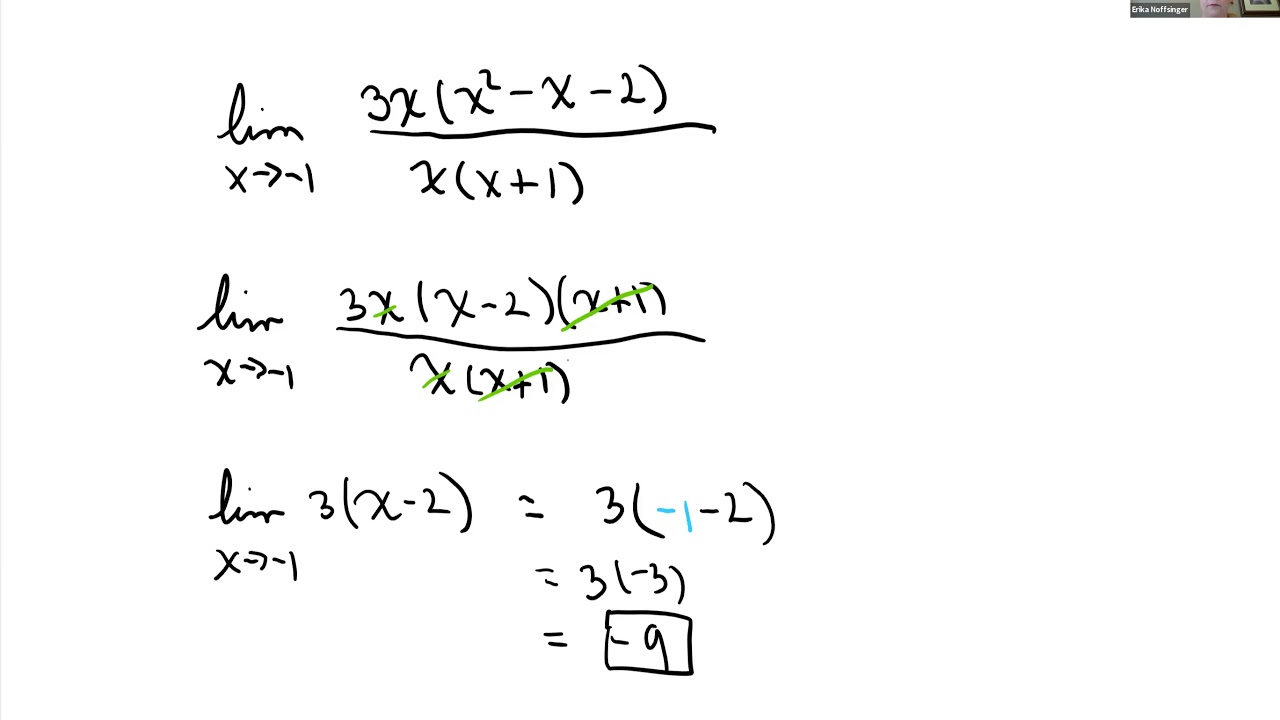
Business and Social Science Calculus Final Exam Review
AP Calculus AB Review

Calculus 2 Final Exam Review -

LIMITS CALCULATOR TECHNIQUES - DIFFERENTIAL CALCULUS | ENGINEERING BOARD EXAM REVIEW | YU JEI ABAT
AP Calculus AB 2003 Multiple Choice (no calculator) - Questions 1-28
5.0 / 5 (0 votes)
Thanks for rating: