Ch. 11.6 Polar Equations of Conics
TLDRThis lecture covers the polar equations of conic sections, focusing on the relationship between conics and polar coordinates. It explains how conics can be easily rotated and shifted using polar equations, and the significance of eccentricity in determining the type of conic section. The parabola is used as a starting point, with the distance from the directrix to a point equating to the distance to the focus. The lecture generalizes the polar equation for all conics and discusses how to identify and graph conic sections based on their eccentricity, providing an example of a hyperbola and its properties.
Takeaways
- 🔍 Conic sections are easier to describe using polar equations.
- 🔄 Polar equations make it simpler to rotate and shift conic sections.
- 🔺 Parabolas are the most basic conic section to study.
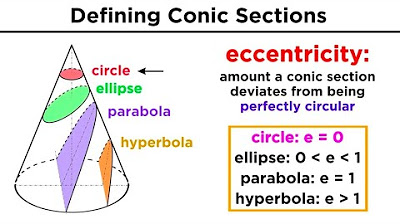
- 📏 Eccentricity is crucial in defining the shape of conic sections in polar coordinates.
- 🟢 A parabola has an eccentricity of 1, an ellipse has an eccentricity between 0 and 1, and a hyperbola has an eccentricity greater than 1.
- 📐 For a parabola, the distance from the directrix to a point is the same as from that point to the focus.
- 🌐 Polar equations of conics can be generalized using the eccentricity (e) and distance (d).
- ⚖️ If the polar equation uses sine, the symmetry axis is the y-axis; if it uses cosine, the symmetry axis is the x-axis.
- 📝 A general conic in polar coordinates is represented as \( r = \frac{ed}{1 \pm e \cos \theta} \) or \( r = \frac{ed}{1 \pm e \sin \theta} \).
- 🔧 To determine the type of conic, manipulate the given polar equation to fit the standard form and identify the eccentricity.
Q & A
What is the main focus of section 11.6 in the transcript?
-The main focus of section 11.6 is to relate conic sections to polar equations, discussing how conics can be more easily described and manipulated using polar coordinates.
Why are polar equations beneficial for describing conic sections?
-Polar equations are beneficial for describing conic sections because they allow for easier rotation around an axis and shifting, making it simpler to discuss these shapes, especially when they involve rotation of axes.
What is the significance of eccentricity in the context of conic sections in polar coordinates?
-Eccentricity is significant because it determines the type of conic section being described. A value close to zero indicates a more circular figure, values between zero and one indicate an ellipse, exactly one indicates a parabola, and values greater than one indicate a hyperbola.
How does the distance from the focus to the directrix relate to the eccentricity of a conic section?
-The distance from the focus to the directrix is directly related to the eccentricity of a conic section. For a parabola, this distance is equal to the point's distance to the directrix, which is why the eccentricity is 1. For ellipses and hyperbolas, the eccentricity is the ratio of this distance to the semi-major axis (a), represented as c/a.
What is the general form of a polar equation for a conic section?
-The general form of a polar equation for a conic section is r = e * d / (1 ± e * cos(θ)) or r = e * d / (1 ± sin(θ)), where e is the eccentricity, d is the distance from the focus to the directrix, and θ is the angle in polar coordinates.
How does changing the sign in the denominator of the polar equation affect the graph of the conic section?
-Changing the sign in the denominator from plus to minus (or vice versa) flips the graph of the conic section across the polar axis, effectively changing its orientation.
What does replacing sine with cosine in the polar equation of a conic section indicate about the axis of symmetry?
-Replacing sine with cosine in the polar equation indicates that the axis of symmetry of the conic section is along the polar axis (x-axis in Cartesian coordinates) instead of the y-axis.
How can you determine the type of conic section from its polar equation?
-You can determine the type of conic section from its polar equation by looking at the value of the eccentricity (e). If e is 1, the conic is a parabola; if e is between 0 and 1, it's an ellipse; and if e is greater than 1, it's a hyperbola.
What is the significance of the vertices in the context of hyperbolas as described in the transcript?
-The vertices of a hyperbola are significant as they represent the points on the hyperbola that are closest to the center, and they help in determining the shape and orientation of the hyperbola in the coordinate plane.
How can you find the foci of a hyperbola given its polar equation?
-You can find the foci of a hyperbola by using the eccentricity and the distance from the center to the vertices. The foci are located at a distance of c (calculated as e * a, where e is the eccentricity and a is the semi-major axis length) from the center along the axis of symmetry.
What is the role of the directrix in the definition of a parabola?
-The directrix is a line that is used to define a parabola. For any point on the parabola, the distance from the point to the focus is equal to the distance from the point to the directrix.
How does the transcript describe the process of graphing a conic section in polar coordinates?
-The transcript describes the process of graphing a conic section in polar coordinates by first identifying the eccentricity and the distance from the focus to the directrix, then using these values to determine the type of conic section and its orientation. It also explains how to find vertices, foci, and the axis of symmetry, which are essential for graphing.
Outlines
📚 Introduction to Polar Equations of Conics
This paragraph introduces the topic of polar equations of conics, focusing on how they relate to conic sections. The instructor explains the ease of describing conic sections using polar equations, especially when dealing with rotations and shifts around an axis. It emphasizes the importance of eccentricity in conic sections when described in polar coordinates, noting how different eccentricity values (接近0 for circles, close to 1 for ellipses, exactly 1 for parabolas, and greater than 1 for hyperbolas) determine the type of conic section. The paragraph sets the stage for a deeper dive into the specifics of parabolas, hyperbolas, and ellipses in polar form.
📐 Understanding Parabolas in Polar Coordinates
The second paragraph delves into the specifics of describing a parabola using polar coordinates. It discusses the relationship between the distance from a point on the parabola to the focus and to the directrix, highlighting the role of eccentricity in defining conic sections. The instructor provides a step-by-step breakdown of how to derive the polar equation of a parabola, emphasizing the significance of the distance 'd' from the directrix to the focus and how altering the sign in the equation affects the orientation of the graph. The paragraph also touches on the implications of changing sine to cosine in the equation, which affects the axis of symmetry.
📉 Generalized Polar Equations for Conics
This paragraph presents the generalized polar equations for conic sections, explaining how the form of the equation changes based on the eccentricity 'e' and whether it's a sine or cosine function. The instructor clarifies that the eccentricity value determines the type of conic section: one for parabolas, values between zero and one for ellipses, and greater than one for hyperbolas. The paragraph also discusses the implications of sine and cosine on the orientation of the conic sections' axes, and how 'd' represents the distance from the directrix to the focus, which varies depending on the type of conic section.
🔍 Analyzing a Hyperbola Example in Polar Coordinates
The fourth paragraph provides an example of a hyperbola in polar coordinates, demonstrating how to manipulate and interpret the given equation to understand the conic's properties. The instructor shows how to identify the eccentricity 'e' and the distance 'd' from the directrix to the focus, using the equation to find the vertices and foci of the hyperbola. It explains the process of determining the center, transverse axis length, and how to calculate additional parameters like 'a', 'b', and 'c' to fully describe the hyperbola, including its orientation and dimensions.
🌐 Rotating and Shifting Conics Using Polar Equations
The final paragraph discusses the benefits of using polar equations for rotating and shifting conic sections. It explains how simple rotations can be achieved by adjusting the angle 'theta' in the polar equation, and how shifts can be represented by modifying the equation accordingly. The paragraph emphasizes the flexibility and ease of using polar coordinates for these transformations, showcasing the power of this approach in analyzing and visualizing conic sections in various orientations and positions.
Mindmap
Keywords
💡Polar Equations
💡Conic Sections
💡Ellipse
💡Hyperbola
💡Parabola
💡Eccentricity
💡Directrix
💡Focus
💡Polar Coordinates
💡Vertices
💡Asymptotes
Highlights
Introduction to polar equations of conics in section 11.6.
Relating conic sections to polar equations for easier rotation and shifting.
Explanation of how polar equations use sines and cosines to represent ellipses.
Difference between polar equations of ellipses, hyperbolas, and parabolas.
Importance of eccentricity in conic sections within polar coordinates.
Eccentricity values defining the type of conic section: circle, ellipse, parabola, or hyperbola.
Description of the right triangle formed by focus (F) and point (P) in conic sections.
Use of cosine and sine in polar equations to represent distances in x and y.
Manipulation of polar equations to isolate r and express conic sections.
Generalized polar equation form for conic sections based on eccentricity.
How the sign in the polar equation affects the orientation of the conic section.
Impact of sine and cosine on the axis of symmetry for conic sections.
Generalized formulas for conic sections in polar coordinates with variable eccentricity.
Explanation of d as the distance from the directrix to the focus in conic sections.
Differentiation between the directrix orientation for parabolas, ellipses, and hyperbolas.
Example problem: Analyzing and graphing a given polar equation of a hyperbola.
Method to find vertices, center, and foci of a hyperbola from its polar equation.
Calculation of the eccentricity and distance c for a hyperbola from its polar equation.
Determination of the transverse axis length and central box dimensions for a hyperbola.
Application of polar equations for simple rotation and shifting of conic sections.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: