RECOGNIZING THE EQUATION AND THE IMPORTANT CHARACTERISTICS OF THE CONIC SECTIONS || PRECALCULUS
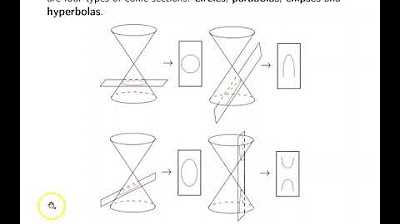
TLDRThis educational video script delves into the world of conic sections, focusing on identifying and transforming equations into their general forms for various shapes: circles, parabolas, ellipses, and hyperbolas. It explains how to recognize the characteristics of each conic by examining the coefficients of x and y terms. The script provides step-by-step examples to demonstrate the process of expanding and simplifying equations into their standard forms, enabling viewers to discern between different types of conic sections based on the signs and values of their coefficients.
Takeaways
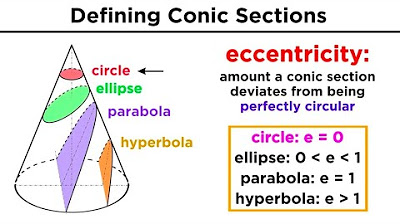
- 📚 The lesson is about recognizing equations and characteristics of conic sections, including circles, parabolas, hyperbolas, and ellipses.
- 🔍 The general form of a circle's equation is \((x-h)^2 + (y-k)^2 = r^2\), where \((h, k)\) is the center and \(r\) is the radius.
- 📐 For a circle centered at the origin, the equation simplifies to \(x^2 + y^2 = r^2\).
- 🔢 The general form of a quadratic equation is \(Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\), where \(A \neq 0\).
- ⭕ To identify a circle, the coefficients of \(x^2\) and \(y^2\) in the equation should be equal and non-zero.
- 📈 The general form of a parabola's equation is \(Ax^2 + Bx + Cy + D = 0\), where either \(A\) or \(B\) is non-zero but not both.
- 👉 The axis of symmetry for a parabola can be found from its standard form equation, such as \(y^2 = 4ax\).
- 🤔 The general form of an ellipse's equation is \(Ax^2 + By^2 + Cx + Dy + E = 0\), where \(A\) and \(B\) have the same sign and are both non-zero.
- 🚀 For hyperbolas, the general form is similar to ellipses but with \(A\) and \(B\) having opposite signs and the product \(AB < 0\).
- 🔄 The process involves expanding the equation, combining like terms, and arranging it into the general form to identify the conic section.
- 👨🏫 Examples are provided throughout the script to demonstrate how to transform and identify different conic sections from their equations.
Q & A
What are the main topics covered in this video lesson?
-The video lesson covers the recognition of equations and important characteristics of conic sections, including circles, parabolas, ellipses, and hyperbolas. It also discusses transforming equations into general form and identifying non-equation conic sections.
What is the general form of the equation of a circle?
-The general form of the equation of a circle is x^2 + y^2 + dx + ey + f = 0, where a ≠ 0. The coefficients of x^2 and y^2 are equal, indicating a circle.
How can you identify if a quadratic equation represents a circle?
-A quadratic equation represents a circle if the numerical coefficients of x^2 and y^2 are equal and non-zero, and the equation is in the general form.
What is the standard form of a parabola's equation?
-The standard form of a parabola's equation is y^2 = 4ax or x^2 = 4ay, where the parabola opens either to the right or left, or up or down, respectively.
How do you transform a standard form equation of a parabola into general form?
-To transform a standard form equation into general form, you expand the equation, combine like terms, and then rearrange the equation so that it matches the general form ax^2 + bx + cy + dy + e = 0.
What is the general form of the equation of an ellipse?
-The general form of the equation of an ellipse is ax^2 + by^2 + cx + dy + e = 0, where both a and b are positive or both are negative, and the coefficients of x^2 and y^2 have the same sign.
How can you determine if a quadratic equation is an ellipse?
-A quadratic equation is an ellipse if the numerical coefficients of x^2 and y^2 are both positive or both negative, indicating that the ellipse is oriented in the same direction along both axes.
What is the general form of the equation of a hyperbola?
-The general form of the equation of a hyperbola is ax^2 + by^2 + cx + dy + e = 0, where the coefficients a and b have different signs, indicating that one axis is stretched relative to the other.
How do you identify a hyperbola from its equation?
-A hyperbola is identified by an equation where the numerical coefficients of x^2 and y^2 have opposite signs, and the product of a and b is less than zero.
What is the process of transforming a given equation into standard form for conic sections?
-The process involves expanding the equation, combining like terms, and then rearranging the terms in descending order of their powers. This allows for the identification of the type of conic section the equation represents.
Can you provide an example of transforming an equation into general form?
-An example given in the script is the equation x^2 + y^2 - 8x + 2y - 33 = 0. After expanding and combining like terms, the general form is identified as x^2 + y^2 - 8x + 2y - 32 = 0.
What is the significance of the coefficients in the general form of conic section equations?
-The coefficients in the general form of conic section equations determine the type of conic section (circle, parabola, ellipse, or hyperbola) and provide information about its orientation, size, and position.
Outlines
📚 Introduction to Conic Sections
This paragraph introduces the topic of conic sections, focusing on the general form of equations for various conic shapes such as circles, parabolas, hyperbolas, and ellipses. It discusses transforming equations into the general form and identifying non-equation conic sections. The general form of a circle is given as \((x-h)^2 + (y-k)^2 = r^2\), and the coefficients of \(x^2\) and \(y^2\) are highlighted as key to identifying a circle's equation. An example equation is provided and transformed into general form, illustrating the process of expanding and combining like terms.
📘 Parabola Equations and Transformations
The second paragraph delves into the equations of parabolas, starting with an example equation that is expanded and simplified into the general form. The process involves expanding squared terms and combining like terms to arrive at the general form \(Ax^2 + Bx + Cy + Dy + E = 0\), where \(A\) and \(B\) are not equal to zero. The axis of symmetry for a parabola is also mentioned, with an example equation transformed to illustrate the steps involved.
📙 Understanding Ellipse Equations
This paragraph discusses the general form of ellipse equations, which is \(Ax^2 + By^2 + Cx + Dy + E = 0\), where both \(A\) and \(B\) are positive or negative. The paragraph provides examples of ellipse equations in standard form and explains how to transform them into the general form. The process involves multiplying through by the denominators and simplifying the equation, which helps in identifying the characteristics of an ellipse.
📒 Hyperbola Equations and Their Characteristics
The fourth paragraph focuses on hyperbolas, presenting the general form of their equations as \(Ax^2 + By^2 + Cx + Dy + E = 0\), where the product of \(A\) and \(B\) is less than zero. The paragraph provides examples of hyperbola equations in standard form and demonstrates how to rearrange and simplify them into the general form. The key is to recognize the signs of the coefficients for \(x^2\) and \(y^2\) to identify a hyperbola.
📕 Identifying Conic Sections from Equations
In this paragraph, the process of identifying conic sections from given equations is explained. It provides examples of equations and shows how to transform them into standard form to determine whether they represent circles, parabolas, ellipses, or hyperbolas. The importance of the coefficients of \(x^2\) and \(y^2\) in determining the type of conic section is emphasized.
📗 Final Examples and Summary
The final paragraph wraps up the lesson with additional examples of conic section equations and their transformations into standard form. It includes equations for circles, ellipses, and hyperbolas, demonstrating the process of completing the square and simplifying equations. The paragraph ends with a reminder to like, subscribe, and hit the bell button for more video tutorials, emphasizing the educational value of the content.
📓 Conclusion and Call to Action
The concluding paragraph serves as a brief closing note, thanking viewers for watching and encouraging them to engage with the content by liking, subscribing, and activating notifications for future videos. It positions the channel as a guide for learning and understanding mathematical concepts related to conic sections.
Mindmap
Keywords
💡Conic Sections
💡General Form
💡Circle
💡Parabola
💡Ellipse
💡Hyperbola
💡Coefficients
💡Standard Form
💡Axis of Symmetry
💡Equation Transformation
💡Numerical Coefficient
Highlights
Introduction to recognizing the equation and characteristics of conic sections.
Discussion on transforming different equations to the general form for conic sections.
Explanation of the general form of a circle and its equation.
Identification of a circle's center and its equation when the center is at the origin.
Coefficients of x and y terms help identify if a quadratic equation represents a circle.
Example of transforming an equation into the general form of a circle.
Process of expanding and simplifying equations to identify conic sections.
General form of the equation for a parabola and its characteristics.
Examples of transforming standard form equations into general form for parabolas.
General form and identification of an ellipse from its equation.
Explanation of the conditions for an equation to be classified as an ellipse.
Examples of converting equations into general form for ellipses.
Introduction to the general form of the equation for a hyperbola.
Conditions that determine if an equation represents a hyperbola.
Examples of transforming equations into general form for hyperbolas.
Identification of conic sections based on coefficients a, b, c, d, and e.
Final summary of the process for identifying conic sections from their equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: