The essence of calculus
TLDRIn this introductory video of a calculus series, Grant aims to demystify the subject by exploring the core concepts of integrals and derivatives through a visual and intuitive approach. Starting with the geometry of a circle and its area, the video guides viewers to understand the derivation of the area formula (pi * r^2) and introduces the ideas of approximating areas under curves and the relationship between integrals and derivatives. The goal is to make viewers feel as if they could have invented calculus by understanding the origins and meanings of its fundamental concepts.
Takeaways
- 📚 The series aims to deeply understand calculus by exploring its core ideas through a visual approach.
- 🌀 The goal is to make viewers feel they could have invented calculus by understanding the origin and meaning of its concepts.
- 📈 Calculus involves many rules and formulas, such as derivatives, the product rule, chain rule, and Taylor series.
- 🔍 The video starts with the exploration of the area of a circle to illustrate the fundamental ideas of calculus.
- 🤔 The area of a circle (πr²) is examined to understand the reasoning behind the formula.
- 🔶 The concept of slicing a circle into concentric rings and approximating each as a rectangle leads to the idea of integrals.
- 📊 By approximating rings as rectangles and summing their areas, the aggregate forms an approximation of the area under a graph.
- 🌟 The process of refining approximations (smaller 'dr') leads to the precise area under the graph, illustrating the power of calculus.
- 🔄 The interplay between integrals and derivatives, where integrals can be reframed as finding the area under a graph, is highlighted.
- 🚀 The derivative, a measure of sensitivity to input changes, is introduced as a key concept in solving integral problems.
- 💡 The fundamental theorem of calculus, which connects integrals and derivatives as inverse operations, is mentioned as a core concept.
Q & A
What is the main goal of the video series on calculus?
-The main goal of the video series is to help viewers understand the core ideas of calculus so deeply that they feel like they could have invented calculus themselves, using a visual approach to clarify the origins and meanings of its concepts.
How does the presenter plan to approach the teaching of calculus?
-The presenter plans to approach the teaching of calculus by focusing on the core ideas and explaining where they come from and what they really mean, rather than just memorizing rules and formulas.
What is the significance of the area of a circle in the video?
-The area of a circle is used as a starting point to explore the core ideas of calculus, such as integrals, derivatives, and their relationship, by thinking deeply about why the area is pi times the radius squared.
How does the presenter illustrate the concept of slicing a circle into rings to find its area?
-The presenter illustrates this concept by imagining the circle sliced into many concentric rings, approximating each ring as a thin rectangle, and then adding up the areas of these rectangles to approximate the total area of the circle.
What is the role of the variable 'dr' in the approximation of the circle's area?
-In the approximation, 'dr' represents a tiny difference in the radius from one ring to the next and is used to express the area of each thin rectangle, which collectively approximate the total area of the circle.
How does the presenter transition from the approximation of the circle's area to the concept of integrals?
-The presenter transitions from the approximation by considering the sum of the areas of the rectangles as the area under the graph of the function 2 pi r, which leads to the concept of integrals as the area under a curve.
What is the significance of the function a(x) in the context of the parabola x^2?
-The function a(x) represents the area under the parabola x^2 between 0 and x, which is an integral that the presenter aims to explore further in the series.
How does the concept of derivatives emerge in the discussion?
-The concept of derivatives emerges when discussing the relationship between small changes in the input (x) and the resulting small changes in the output (a), which is approximately equal to the value of the function x^2 at that point.
What is the fundamental theorem of calculus mentioned in the video?
-The fundamental theorem of calculus is the principle that ties together integrals and derivatives, showing how each one is the inverse of the other, and it is key to solving problems that involve finding the area under a curve or the original function from its derivative.
How does the presenter encourage the development of a deeper understanding of calculus?
-The presenter encourages a deeper understanding by urging viewers to think like mathematicians, to ponder the ideas, and to explore the concepts visually and intuitively, as if they were inventing the subject from scratch.
What is the role of Patreon supporters in the creation of this series?
-Patreon supporters provide financial backing and suggestions during the development of the series. They receive early access to the videos, and their support contributes to the presenter's ability to create the content.
Outlines
📚 Introduction to Calculus
The video introduces the essence of calculus, aiming to explain the core ideas in a way that makes viewers feel they could have invented calculus themselves. It sets the stage for a 10-day video series, with each video focusing on a different aspect of calculus, starting with the exploration of the area of a circle to lead into integrals, derivatives, and their relationship.
📊 Approximating the Area of a Circle
The video uses the example of finding the area of a circle to illustrate the concepts of integrals and the approximation of areas through summing up small quantities. By dividing the circle into concentric rings and approximating each ring as a rectangle, the video shows how the sum of these approximations can lead to the area under a graph, which in this case, forms a triangle that helps derive the formula for the area of a circle (pi * r^2).
🔄 The Relationship Between Integrals and Functions
The video delves into the relationship between the area under a graph and the function defining that graph. It introduces the concept of an integral as a function that gives the area under a parabola, such as x^2, between two points. The video emphasizes the importance of understanding the interplay between the function and its integral, setting the stage for the concept of derivatives and their role in solving integral problems.
📈 Derivatives and the Fundamental Theorem of Calculus
The video introduces derivatives as a measure of how sensitive a function is to small changes in its input. It explains how the derivative of a function can be used to reverse engineer the original function from its integral. The video concludes by highlighting the fundamental theorem of calculus, which connects integrals and derivatives, showing that they are inverse operations. The video also acknowledges the support of Patreon contributors and their role in the development of the series.
Mindmap
Keywords
💡Calculus
💡Integrals
💡Derivatives
💡Geometry
💡
💡Pi (π)
💡Concentric Rings
💡Symmetry
💡Approximation
💡Visual Approach
💡Fundamental Theorem of Calculus
Highlights
The series aims to provide an in-depth understanding of calculus, making complex concepts accessible through a visual approach.
The presenter's objective is to help viewers feel as if they could have invented calculus themselves by understanding the origins and meanings of its core ideas.
Calculus is often associated with numerous rules and formulas, such as derivatives, the product rule, chain rule, and Taylor series, which are typically memorized.
The video introduces the concept of integrals and derivatives, and how they are opposites, through the exploration of the area of a circle.
The area of a circle is explained not just as a formula, but as a result of understanding the geometric relationship between the circle's radius and pi.
The method of slicing a circle into concentric rings and approximating each as a rectangle provides a visual way to understand the area calculation.
The concept of approximating shapes and areas through infinitesimally small pieces (rings of thickness dr) is introduced.
The sum of the areas of many thin rectangles approximates the area under a graph, leading to the concept of integration.
The integral of a function is likened to the area under its graph, providing a geometric interpretation of integral calculus.
The process of breaking down complex problems into the sum of many small quantities is a fundamental approach in calculus.
The relationship between the change in the area under a graph and the function defining the graph leads to the concept of derivatives.
Derivatives are introduced as a measure of sensitivity to changes in input, with applications in solving integral problems.
The fundamental theorem of calculus is mentioned, highlighting the inverse relationship between integrals and derivatives.
The video emphasizes the importance of visualizing mathematical concepts and encourages a playful exploration of ideas.
The presenter expresses gratitude to Patreon supporters for their financial backing and early access to the series.
The series is designed to be engaging and educational, aiming to make viewers feel like they are part of the process of mathematical discovery.
Transcripts
Browse More Related Video
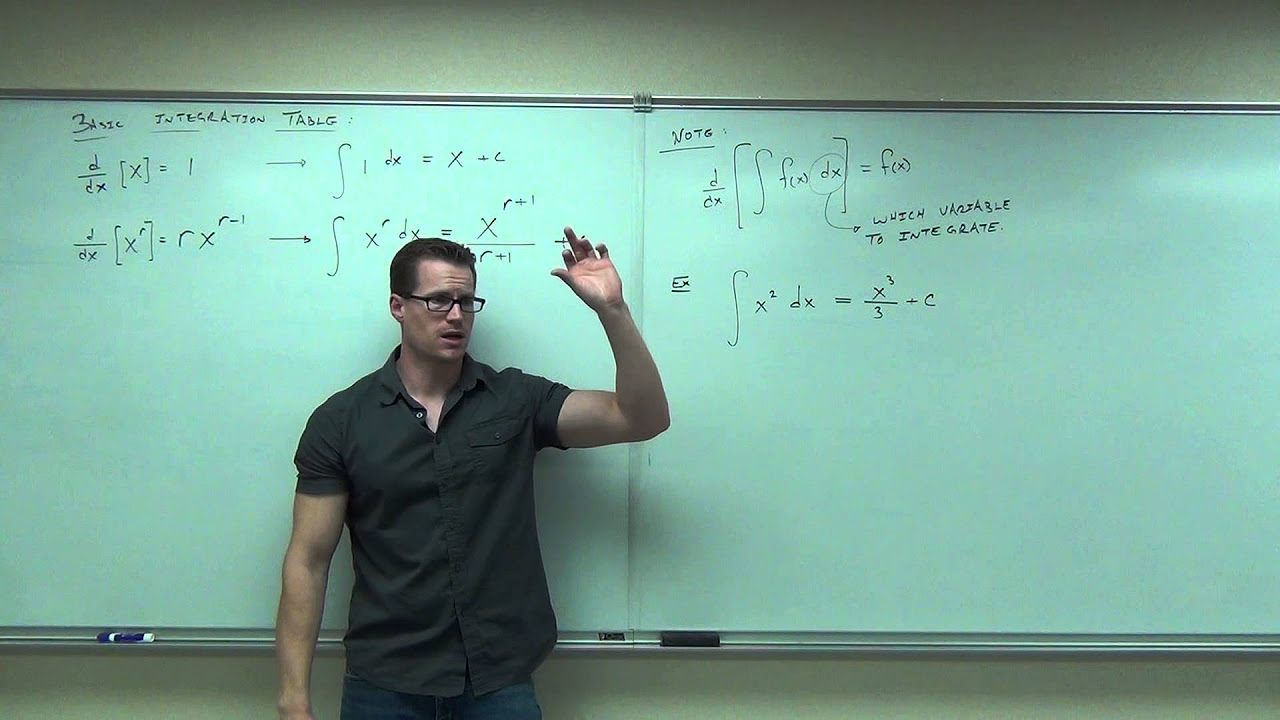
Calculus 1 Lecture 4.1: An Introduction to the Indefinite Integral

Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions

Finding The Area Under The Curve Using Definite Integrals - Calculus

Lecture 01: Two Ideas, Vast Implications
Definite Integrals (part 4)

Calculus AB/BC – 6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
5.0 / 5 (0 votes)
Thanks for rating: