AP Calculus AB - 10 Minute Recap
TLDRThis comprehensive review covers key AP Calculus AB topics, including limits, continuity, derivatives, and integrals. It emphasizes understanding limit definitions, basic derivative rules, and the applications of derivatives in optimization and related rates. The importance of knowing Riemann sums, the fundamental theorem of calculus, and applications in areas and volumes of revolution is highlighted. The review also touches on theorems like intermediate value and mean value theorems, and the necessity of invoking continuity conditions when applying them.
Takeaways
- 📈 Start with understanding limits and continuity, ensuring the limit exists from both left and right and matches the function's value at that point for continuity.
- 🔢 Use L'Hopital's rule for evaluating limits when encountering indeterminate forms like 0/0 or ∞/∞, and consider the sign of the resulting infinity.
- 📌 Identify horizontal asymptotes by examining limits at positive and negative infinity, noting that functions can have different asymptotes.
- 🌀 Recognize that a function is differentiable if it is continuous, with exceptions like corners, cusps, or undefined points where the derivative does not exist.
- 🔍 Apply implicit differentiation to equations where you cannot solve for y directly, resulting in dy/dx in terms of both x and y.
- 📊 Understand applications of derivatives: find tangent lines with slope and point, and analyze increasing/decreasing functions and concavity through first and second derivative tests.
- 🏆 Focus on optimization and related rates, though not heavily tested on the AP exam, knowing how to set up and solve for maximum or minimum values and related rates.
- 📝 Be proficient with Riemann sums and trapezoid sums for integration, understanding their accuracy as estimates depending on the function's concavity and monotonicity.
- 🌆 Apply integration to find areas between curves, and be familiar with volumes of revolution using the disk and washer method, focusing on the correct orientation of rectangles.
- 🚀 Relate integrals to rates of change and motion, using the fundamental theorem of calculus to find net changes and analyze velocities and accelerations for direction and speed.
- 📚 Know how to solve differential equations by separation of variables, and be able to sketch slope fields and particular solutions by determining the value of the constant c.
Q & A
What is the condition for a limit to exist?
-A limit only exists if it approaches the same value from both the left and the right.
What should you do first when evaluating limits?
-Always plug in the value first to evaluate the limit.
When should you use L'Hopital's Rule in evaluating limits?
-You should use L'Hopital's Rule when you get an indeterminate form like 0/0 or ∞/∞.
What are the two conditions for a function to be considered continuous?
-A function is continuous if the limit exists from the left and the right, and the value of the function matches what the limit approaches at that point.
What is the significance of the derivative in determining if a function is increasing or decreasing?
-A function is increasing if its derivative is greater than zero and decreasing if its derivative is less than zero.
How do you find the equation of a tangent line?
-To find the equation of a tangent line, you need two pieces of information: the slope of the line (which comes from the derivative at a specific point) and a point on the line (either given or found by plugging an x value into the function to get the y value). Then, use the slope-point form to write the equation.
What is the main concept behind implicit differentiation?
-Implicit differentiation is used when you can't solve for y directly. Instead, you take the derivative of both sides of an equation, treating y as a function of x (dy/dx), with the goal of isolating dy/dx and solving for it.
How do you determine if a function is eligible for using the disk and washer method for volumes?
-The disk and washer method is used for volumes of revolution. It is applicable when calculating volumes by revolving a shape around an axis, and the shape must be such that it can be sliced into disks or washers with uniform thickness.
What is the fundamental theorem of calculus and its two forms?
-The fundamental theorem of calculus states that when you integrate, you take the antiderivative, plug in the endpoints, and subtract. The two forms are: 1) for definite integrals, where you integrate a function and find the difference between the values of the antiderivative at the endpoints, and 2) for antiderivatives of functions with x terms, where you integrate and then plug in the bounds of the integral, applying the chain rule if necessary.
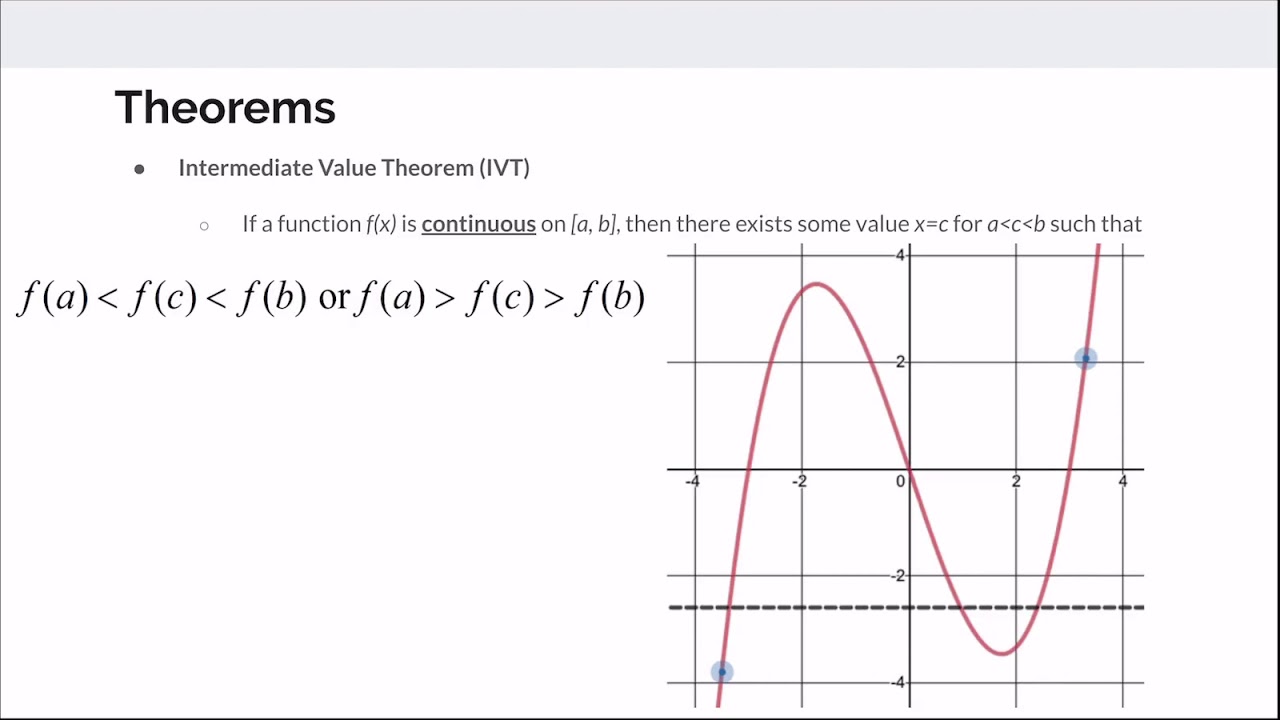
What are the conditions required for the Extreme Value Theorem, Intermediate Value Theorem, and Mean Value Theorem to hold?
-All three theorems require the function to be continuous. The Mean Value Theorem additionally requires the function to be differentiable over the regions in question.
How do you interpret the integral of velocity and the integral of the absolute value of velocity?
-The integral of velocity represents the displacement or change in position. The integral of the absolute value of velocity represents the speed, which is the total distance traveled.
Outlines
📚 Introduction to AP Calculus AB Review
The video script begins with an overview of key concepts in AP Calculus AB, emphasizing the importance of understanding limits and continuity. It highlights the need to recognize limits from both the left and right and the conditions under which a limit exists. The script provides strategies for evaluating limits, such as plugging in values and applying L'Hopital's rule for indeterminate forms. It also touches on the concept of horizontal asymptotes and the criteria for a function to be considered continuous. The segment concludes with a brief mention of derivatives, differentiability, and the significance of understanding the limit definitions and basic derivative rules, including the product, quotient, and chain rules.
📈 Derivatives and Applications in AP Calculus AB
This paragraph delves deeper into the applications of derivatives in AP Calculus AB. It covers the definition of the derivative, the importance of understanding the limit definition, and the basic rules of differentiation. The script discusses the concept of differentiability and the conditions under which a function is not differentiable, such as discontinuity, corners, cusps, or undefined points. It also explains implicit differentiation and its process, as well as the applications of derivatives in finding tangent lines, understanding curve behavior, and identifying relative minimums and maximums through the first and second derivative tests. The paragraph concludes with a brief overview of optimization and related rates, noting that these topics are not heavily tested on the AP exam.
🧮 Integration and Theorems in AP Calculus AB
The final paragraph of the script focuses on integration and key theorems in AP Calculus AB. It emphasizes the importance of understanding Riemann sums, the trapezoid rule, and the fundamental theorem of calculus. The script explains how to handle integral bounds that are functions of x and provides insights into the applications of integration, such as calculating areas between curves and volumes of revolution. It also touches on the disk and washer method for volumes and the concept of cross-sectional areas. The paragraph concludes with a review of three key theorems: the extreme value theorem, the intermediate value theorem, and the mean value theorem, highlighting the conditions required for their application and a brief overview of how they function within the context of the course.
Mindmap
Keywords
💡Limits
💡Continuity
💡Derivatives
💡Differentiability
💡Integration
💡Applications of Derivatives
💡Volumes of Revolution
💡Theorems
💡Differential Equations
💡Optimization
💡Related Rates
Highlights
Start with limits and continuity, emphasizing limits from the left and right and the conditions for a limit to exist.
For evaluating limits, always plug in the value first and use L'Hopital's rule for indeterminate forms like 0/0 or ∞/∞.
Horizontal asymptotes are limits at infinity and can be different for positive and negative directions.
A function is continuous if the limit approaches the function's value at that point, meaning no breaks or gaps.
Understand the limit definition of the derivative and basic derivative rules, including product, quotient, and chain rules.
Know when a function is not differentiable, such as at corners, cusps, or points of discontinuity.
Implicit differentiation involves taking derivatives of both sides of an equation when you can't solve for y directly.
Logarithmic differentiation involves taking the natural log of both sides and then performing implicit differentiation.
For applications of derivatives, understand how to find the equation of a tangent line using slope and point.
Know how to determine if a function is increasing or decreasing and understand concavity through the first and second derivative tests.
Points of inflection are where the concavity changes, and absolute min/max are found using the candidate's test.
Optimization and related rates are not heavily tested on the AP Calculus exam but understand the basic concepts.
For integration, know how to perform Riemann sums and understand the fundamental theorem of calculus in both forms.
In Riemann sums, understand whether the sums are underestimates or overestimates based on the function's concavity and monotonicity.
Know how to calculate areas between curves and volumes in general, with a focus on disk and washer methods for volumes of revolution.
Understand the net rate of change and how to apply it to various scenarios, such as water flowing in and out of a tank.
Be familiar with the interpretation of integrals of velocity for displacement and speed, and how to determine the direction of motion based on the sign of velocity.
Know how to solve separation of variables in differential equations and the difference between general and particular solutions.
Understand the three key theorems: intermediate value, mean value, and extreme value theorems, and their requirements for continuity and differentiability.
Be prepared for different types of free response questions (FRQs) on the AP exam, including those involving data tables, net change, and curve features.
Transcripts
Browse More Related Video

What We Must Know for Calculus AB
AP Calculus AB Review

💥💥💥Stuff You MUST Know Cold for the AP Calculus AB Exam💥💥💥[EVERYTHING YOU NEED TO KNOW] 2021

🚨EXPERT 🚨Tips for How to Get a 💥5 on the 2022 AP Calculus AB Exam💥 [What You REALLY Need to Know]

Using IVT, MVT, and EVT

AP Calculus Multiple Choice Practice Test (2020 AP CED Problems)
5.0 / 5 (0 votes)
Thanks for rating: