Ch. 11.2 Ellipses
TLDRThis educational video script delves into the concept of ellipses, a type of conic section formed by an angled intersection with a conic. It explains the properties of ellipses, including their two foci, constant sum of distances from any point on the ellipse to the foci, and the major and minor axes. The script also covers how to derive the equation of an ellipse and introduces the concept of eccentricity, which describes the shape's roundness. Practical applications, such as modeling orbits in space, are discussed, with an example calculating the orbit of Apollo 11 around the moon, illustrating the mathematical relevance of ellipses in real-world scenarios.
Takeaways
- 📚 The script is a lecture on ellipses, a type of conic section formed by an angled plane intersecting a cone, resulting in a stretched-out circle.
- 📏 An ellipse has two focal points, or 'foci', denoted as F1 and F2, and the sum of the distances from any point on the ellipse to each focus is constant.
- 🔍 The major and minor axes of an ellipse are the longest and shortest distances across the ellipse, respectively, with the major axis always being the longer one.
- 📐 The vertices of an ellipse are the endpoints of the major axis, and the foci are always located on the major axis, equidistant from the center.
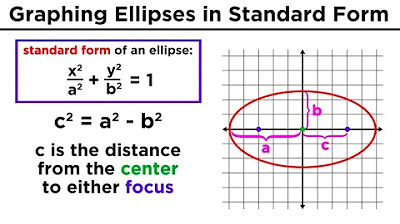
- 📈 The standard form of the equation for an ellipse can indicate which axis is the major axis by having the larger constant under the squared variable.
- 🧩 The lengths of the semi-major axis (a) and semi-minor axis (b) can be found directly from the standard form equation, but finding the distance to the foci (c) requires using the Pythagorean theorem, c² = a² - b².
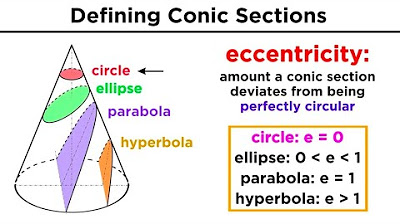
- 🔄 Eccentricity (e) of an ellipse is the ratio of the distance from the center to a focus (c) over the semi-major axis (a), and it indicates how elongated the ellipse is, with values ranging from 0 (circle) to 1 (highly elongated).
- 🚀 The script provides an example of applying ellipses to model the elliptical orbits of celestial bodies, such as the orbit of the Apollo 11 spacecraft around the Moon.
- 📉 The vertices, foci, and other characteristics of an ellipse can be determined by manipulating and analyzing its equation in standard form.
- 📊 The script demonstrates how to find the equation of an ellipse given certain parameters, such as the distances from the center to the vertices and foci, using the Apollo 11 lunar orbit as an example.
- 🌐 The lecture concludes by emphasizing the ubiquity of ellipses in various applications, from modeling orbits in space to everyday objects, and the importance of understanding their properties.
Q & A
What is an ellipse?
-An ellipse is a stretched-out circle formed when an angled plane intersects a conic section, resulting in an elongated shape that is not parallel to the base or the slope of the cylindrical side.
What are the two foci of an ellipse?
-An ellipse has two foci, denoted as f1 and f2, which are points inside the ellipse such that the sum of the distances from any point on the ellipse to each focus is constant.
What is the major axis and the minor axis of an ellipse?
-The major axis is the longest distance between two points on the ellipse, and the minor axis is the shortest distance between two points. Both axes pass through the center of the ellipse.
How are the vertices of an ellipse defined?
-The vertices of an ellipse are the endpoints of the major axis, located at a distance 'a' from the center along the major axis.
Where are the foci of an ellipse located?
-The foci of an ellipse are always located on the major axis and are equidistant from the center of the ellipse.
What is the relationship between the lengths of the major axis (a), the minor axis (b), and the distance to the foci (c) in an ellipse?
-The relationship is given by the equation c^2 = a^2 - b^2, which can be used to find the distance to the foci if the lengths of the major and minor axes are known.
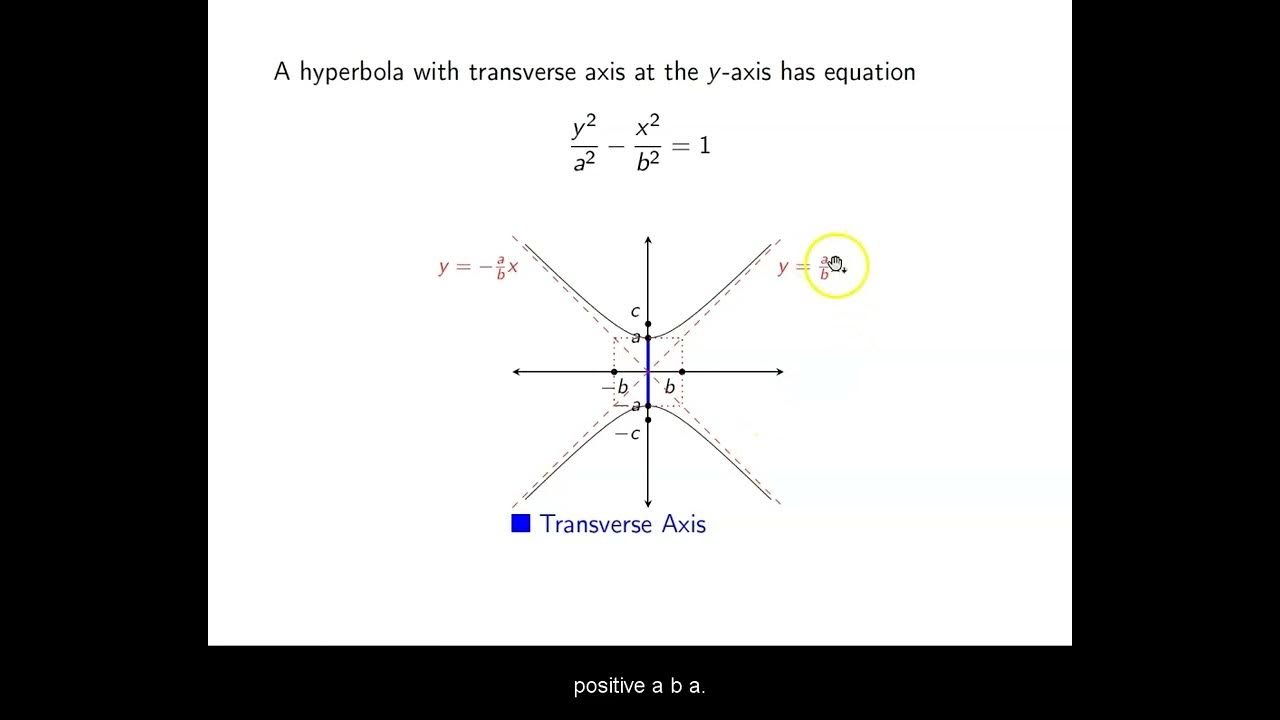
How can you determine the orientation of an ellipse from its equation?
-The orientation of an ellipse can be determined from its equation by identifying which variable (x or y) has the larger constant under it in the standard form; this indicates the major axis.
What is the eccentricity of an ellipse and what does it represent?
-The eccentricity (e) of an ellipse is the ratio of the distance from the center to a focus (c) over the distance from the center to a vertex (a). It represents how elongated the ellipse is, with values closer to 0 indicating a shape closer to a circle, and values closer to 1 indicating a more elongated shape.
How can you find the equation of an ellipse given its major and minor axes lengths?
-Given the lengths of the major axis (2a) and minor axis (2b), you can write the equation of the ellipse in standard form as (x^2/a^2) + (y^2/b^2) = 1 if the major axis is horizontal, or (y^2/a^2) + (x^2/b^2) = 1 if the major axis is vertical.
What is an example of an application of ellipses in real life?
-Elliptical orbits are a common application of ellipses in real life, as many celestial bodies, including satellites and planets, follow elliptical paths around others due to gravitational influences.
How can you derive the equation for the orbit of a spacecraft like Apollo 11 around the Moon?
-You can derive the equation for the orbit by knowing the distances from the spacecraft to the Moon at its closest (perilune) and furthest (apolune) points, as well as the radius of the Moon. Using these, you can calculate the lengths of the major and minor axes and then apply the standard form of the ellipse equation.
Outlines
📚 Introduction to Ellipses and Their Properties
This paragraph introduces the concept of an ellipse as a conic section formed by an angled plane intersecting a cone. It distinguishes an ellipse from a circle by explaining that an ellipse is an elongated circle due to the non-parallel orientation of the intersecting plane. The paragraph also introduces the terms 'focus' and 'foci', explaining that an ellipse has two foci and the constant sum of distances from any point on the ellipse to each focus. It describes the major and minor axes of an ellipse, their lengths, and how they pass through the ellipse's center. The orientation of the ellipse and the axes is also discussed, with examples of how the major axis can be aligned with or rotated relative to the coordinate axes.
📐 Understanding the Geometry of Ellipses
The second paragraph delves deeper into the geometry of ellipses, discussing the relationship between the ellipse's foci, vertices, and axes. It explains how the major axis is the longest distance across the ellipse and the minor axis is the shortest, with both axes intersecting at the ellipse's center. The paragraph provides a detailed explanation of how to determine the location of the foci in relation to the major axis and introduces the concept of using the Pythagorean theorem to find the distance 'c' from the center to the foci, given the lengths of the semi-major axis 'a' and the semi-minor axis 'b'. It also touches on the derivation of the ellipse equation based on the constant sum of distances from a point on the ellipse to the foci.
📘 Standard Equation of an Ellipse and Its Characteristics
This paragraph focuses on the standard equation of an ellipse and how it can be used to determine the lengths of the semi-major and semi-minor axes, as well as the orientation of the ellipse. It explains that the larger denominator under the squared variables indicates the major axis and its corresponding vertex location. The paragraph provides an example of how to manipulate an equation into the standard form to identify the values of 'a' and 'b', and how to find the foci's location using the values of 'a' and 'b'. It also discusses the eccentricity of an ellipse, which is a measure of how elongated the ellipse is, and how it relates to the distance between the foci and the vertices.
🚀 Application of Ellipses in Orbital Mechanics
The fourth paragraph applies the concept of ellipses to orbital mechanics, describing how most orbits in space are elliptical, including those of the moon, satellites, and planets. It uses the historical example of the Apollo 11 mission's lunar orbit to illustrate how to derive the equation of an elliptical orbit. The paragraph explains the terms 'perilune' and 'apolune', referring to the closest and furthest points of an orbit from the celestial body, respectively. It provides a step-by-step calculation to find the equation of Apollo 11's orbit around the moon, considering the moon's radius and the spacecraft's distances at perilune and apolune.
🛰 Calculating the Orbital Parameters of Apollo 11
This paragraph continues the application of ellipses in orbital mechanics by calculating the specific parameters of Apollo 11's orbit around the moon. It explains how to determine the length of the major axis and the location of the foci using the given distances from the moon's surface at perilune and apolune, as well as the moon's radius. The paragraph demonstrates the process of finding the semi-major axis 'a', the semi-minor axis 'b', and the distance 'c' to the foci by manipulating the standard form of the ellipse equation and applying the Pythagorean theorem.
📉 Eccentricity and Orbital Shape of Apollo 11
The final paragraph discusses the concept of eccentricity in the context of Apollo 11's orbit, explaining its significance in determining the shape of the orbit and how circular or elongated it is. It provides a brief analysis of the eccentricity based on the calculated values of 'a' and 'c', and comments on the near-circular nature of the orbit due to the small difference between the squares of 'a' and 'b'. The paragraph concludes with a general observation on the importance of understanding ellipses in various applications, including space orbits.
Mindmap
Keywords
💡Ellipse
💡Conic Section
💡Focus (Foci)
💡Major Axis
💡Minor Axis
💡Vertices
💡Eccentricity
💡Perilune (Perilum)
💡Apolune (Apolloon)
💡Orbit
💡Pythagorean Theorem
Highlights
Introduction to conic sections with a focus on ellipses, which are formed by an angled plane intersecting a conic section.
Explanation of an ellipse as a stretched-out circle, differing from a perfect circle due to the angle of intersection with the conic section.
Discussion of the two foci (foci) of an ellipse and their significance in defining the shape.
The constant sum of distances from any point on the ellipse to the two foci, defining a unique property of ellipses.
Introduction of the major and minor axes of an ellipse, explaining their roles in determining the ellipse's shape and orientation.
Description of the vertices of an ellipse, which are the endpoints of the major axis.
Location of the foci on the major axis, equidistant from the center of the ellipse.
Use of the Pythagorean theorem to find the distance from the center to the foci (c), given the lengths of the major (a) and minor (b) axes.
Differentiation between the equations of an ellipse based on which axis is the major or minor.
Method to determine the major and minor axes from the standard form of an ellipse's equation.
Example problem demonstrating how to manipulate an ellipse's equation into the standard form and identify key features.
Explanation of eccentricity (e) as the ratio of the distance from the center to the foci (c) over the semi-major axis (a).
Application of ellipses in modeling orbits, such as those of satellites and planets.
Real-world example of calculating the orbit of Apollo 11 around the moon using the properties of an ellipse.
Calculation of the length of the major axis and the distance of the foci for the Apollo 11 lunar orbit.
Determination of the minor axis length and the eccentricity of the Apollo 11 orbit using the Pythagorean theorem.
Observation that the Apollo 11 orbit is close to circular due to the small difference between the major and minor axes.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: