Find and Classify all Critical Points of a Multivariable Function

Nakia Rimmer
20 Jul 202009:48
EducationalLearning
32 Likes 10 Comments

TLDRIn this instructional video, Nakiya Rimmer guides viewers through a multivariable optimization problem. The process begins with finding critical points of a given polynomial function using partial derivatives set to zero. The video demonstrates how to factor and solve these equations to identify potential maximum and minimum points. It then introduces the concept of classifying these points using second partial derivatives, specifically through the Hessian matrix and discriminant. The example provided walks through the steps of calculating and interpreting the Hessian to determine whether a point is a local maximum, minimum, or saddle point. The video concludes with a brief mention of extending these concepts to find absolute maxima and minima within a defined interval.

Takeaways
  • 📚 The video is an educational tutorial focused on multivariable optimization, specifically finding and classifying critical points of a function.
  • 📈 The function in question is a polynomial represented visually using a three-dimensional graph in GeoGebra, which has a defined maximum and minimum.
  • 🔍 The process starts by finding the first partial derivatives with respect to x and y, and setting them equal to zero to find potential critical points.
  • 📝 The video demonstrates factoring and solving the partial derivatives, resulting in two cases: 6x = 0 and y - 1 = 0, leading to the discovery of critical points.
  • 🔢 The critical points found are (0,0), (0,2), (1,1), and (-1,1), which are then classified based on second partial derivatives.
  • 📉 The Hessian matrix, or discriminant, is introduced for classifying the critical points, which includes the second partial derivatives.
  • 📌 The video explains that the sign of the discriminant and the sign of the double x partial derivative are used to classify the critical points as local maxima, minima, or saddle points.
  • 📊 The origin (0,0) is identified as a local maximum, (0,2) as a local minimum, and the points (1,1) and (-1,1) as saddle points based on the discriminant and second derivative tests.
  • 🔍 The tutorial emphasizes the importance of plugging the critical points back into the function to verify their classification.
  • 🎓 The presenter, Nakiya Rimmer, provides a step-by-step guide and encourages viewers to practice the process themselves, indicating that this is a foundational concept in multivariable calculus.
  • 👋 The video concludes with an invitation for viewers to like, subscribe, and comment with any questions, and a promise of further exploration in future videos.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is multivariable optimization, specifically finding and classifying critical points of a given function.

  • What is the function in the example provided in the video?

    -The function is a polynomial in nature, but the specific form is not provided in the transcript. It is visualized as a three-dimensional graph using GeoGebra.

  • What does the three-dimensional graph of the function look like according to the video?

    -The graph has a defined maximum and minimum, with two other points resembling a bull's horns, indicating potential critical points.

  • What is the first step in finding critical points in multivariable optimization?

    -The first step is to find the partial derivatives with respect to each variable, in this case, with respect to x and y.

  • How does one find the critical points from the partial derivatives?

    -You set the partial derivatives equal to zero and solve for the variables, factoring if possible, to find the critical points.

  • What is the significance of the second derivative in classifying critical points?

    -The second derivative, or second partials, are used to classify critical points by creating a formula called the discriminant or Hessian, which helps determine if a point is a local maximum, local minimum, or a saddle point.

  • What is the discriminant or Hessian in the context of multivariable optimization?

    -The discriminant or Hessian is a formula that incorporates the second partial derivatives and helps in classifying the critical points based on their concavity.

  • How many critical points are found in the example in the video?

    -Four critical points are found in the example: (0,0), (0,2), (1,1), and (-1,1).

  • How are the critical points classified in the video?

    -The critical points are classified by plugging them into the Hessian formula and checking the sign of the discriminant and the sign of the second derivative with respect to x.

  • What does the video suggest for the next steps after learning about local maxima and minima?

    -The video suggests that the next steps will involve finding absolute maxima and minima, which may require checking critical points on an interval and at the endpoints.

  • Who is the presenter of the video?

    -The presenter of the video is Nakiya Rimmer.

Outlines
00:00
📚 Introduction to Multivariable Optimization

This paragraph introduces the topic of multivariable optimization, focusing on finding and classifying critical points of a given function. The speaker uses a simple polynomial function as an example and presents a three-dimensional graph created with GeoGebra to visually identify potential maximum and minimum points. The process begins by taking the partial derivatives with respect to x and y, setting them equal to zero, and solving for the variables. The example provided walks through factoring out common terms and solving for x and y to find the critical points. The paragraph emphasizes the importance of understanding both the process of finding critical points and classifying them based on second derivatives, which will be discussed in subsequent parts of the video.

05:02
🔍 Classifying Critical Points Using Second Derivatives

In this paragraph, the focus shifts to classifying the critical points found in the previous section. The speaker explains the use of second partial derivatives and the Hessian matrix, also known as the discriminant, to determine the nature of the critical points. The process involves calculating the second partial derivatives with respect to x (d^2x) and y (d^2y), as well as the mixed partial derivative (d^2(xy)). These values are then used to construct the Hessian matrix, which is evaluated at the critical points. The sign of the determinant of this matrix, along with the sign of the second derivative with respect to x, helps classify the points as local maxima, local minima, or saddle points. The speaker provides a step-by-step analysis of each critical point, demonstrating how to plug the points into the function to determine the Z values and classify them accordingly. The paragraph concludes with a brief mention of absolute maximum and minimum problems, setting the stage for further discussion in future videos.

Mindmap
Keywords
💡Multivariable Optimization
Multivariable optimization refers to the process of finding the maximum or minimum values of a function that depends on more than one variable. In the context of the video, the focus is on identifying critical points of a given polynomial function, which are potential candidates for local maxima or minima. The script describes a methodical approach to finding these points by setting the first partial derivatives equal to zero.
💡Critical Points
Critical points are the points on the graph of a function where the derivative is zero or undefined, indicating potential local maxima, minima, or points of inflection. The video script involves finding these points for a given function by solving the equations formed by setting the partial derivatives with respect to each variable to zero.
💡Partial Derivatives
Partial derivatives are the derivatives of a function with respect to each variable, while treating the other variables as constants. In the video, the partial derivatives with respect to 'x' and 'y' are calculated to find the critical points of the function. For example, the partial derivative with respect to 'x' is given as '6x - 6', and with respect to 'y' as '3y^2 - 6y'.
💡Factoring
Factoring is a mathematical technique used to rewrite an expression as the product of its factors. In the script, factoring is used to simplify the equations obtained from setting the partial derivatives to zero, making it easier to solve for the variables. For instance, '6x' is factored out from '6x(y - 1)' to find the values of 'x' and 'y' that make the expression zero.
💡Discriminant
The discriminant is a part of the Hessian matrix used to classify the nature of critical points in multivariable calculus. It is a determinant that includes second partial derivatives of the function. In the video, the discriminant is calculated using the formula involving the second partial derivatives to determine whether a critical point is a local maximum, local minimum, or a saddle point.
💡Hessian Matrix
The Hessian matrix is a square matrix of second-order partial derivatives of a function, used to determine the concavity of the function at a given point. In the video, the Hessian matrix is constructed to classify the critical points. The discriminant, derived from the Hessian, helps in identifying whether the function is concave up or down at the critical points.
💡Second Derivatives
Second derivatives are the derivatives of the first derivatives of a function. They provide information about the curvature of the function at a given point. In the script, second derivatives are used to form the Hessian matrix and are crucial for classifying the critical points as local maxima, minima, or saddle points.
💡Local Maximum/Minimum
A local maximum or minimum is a point on the graph of a function where the function's value is greater than or less than the values of the function in its immediate vicinity. The video script describes a process to determine whether a critical point is a local maximum or minimum by analyzing the sign of the discriminant and the second derivative test.
💡Saddle Point
A saddle point is a critical point of a function of two or more variables where the function does not have a local maximum or minimum. It is characterized by a negative discriminant. In the video, the classification of critical points includes identifying saddle points, which are indicated by a negative value of the discriminant.
💡GeoGebra
GeoGebra is a dynamic mathematics software that allows users to graph functions, create 3D models, and explore mathematical concepts visually. The video script mentions GeoGebra as the tool used to visualize the three-dimensional graph of the function, which helps in understanding the nature of the critical points.
Highlights

Introduction to a multivariable optimization example to find and classify critical points.

Use of a polynomial function visualized with a three-dimensional graph in GeoGebra.

Identification of a defined maximum and minimum in the function's graph.

Explanation of the process to find critical points using partial derivatives.

Factoring out common terms in the partial derivative equations to simplify the process.

Solving for critical points by setting partial derivatives equal to zero.

Case-by-case analysis for different scenarios when partial derivatives are zero.

Finding two critical points (0,0) and (0,2) through the process.

Further exploration for critical points when y equals 1, leading to additional points (1,1) and (-1,1).

Introduction of second derivatives, or second partials, for classifying critical points.

Construction of the Hessian matrix using second partial derivatives.

Explanation of the discriminant function and its role in classifying critical points.

Calculation of the discriminant for each critical point to determine their nature.

Classification of the origin as a local maximum based on the discriminant and second derivative signs.

Identification of (0,2) as a local minimum and (1,1) and (-1,1) as saddle points.

Reinforcement of the process to find and classify critical points using first and second partial derivatives.

Teaser for upcoming content on absolute max and min in multivariable calculus.

Encouragement for viewers to like, subscribe, and comment for further questions.

Transcripts

Browse More Related Video

Find and classify critical points

Use the Second Derivative Test to Find Any Extrema and Saddle Points: f(x,y) = -4x^2 + 8y^2 - 3

Second Derivative Test Multivariable (Calculus 3)

Critical Points of Functions of Two Variables

Local Extrema, Critical Points, & Saddle Points of Multivariable Functions - Calculus 3

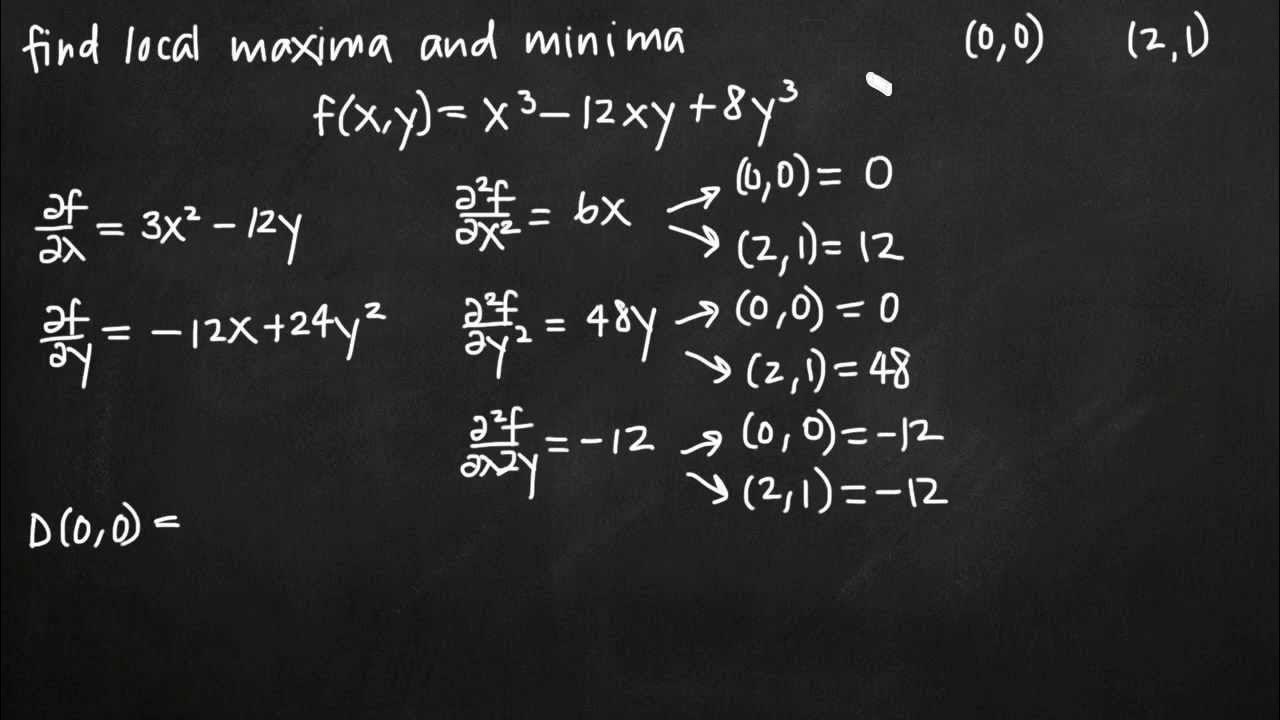
Local extrema and saddle points of a multivariable function (KristaKingMath)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Multivariable CalculusCritical PointsOptimizationPartial DerivativesHessian MatrixDiscriminantGeogebraEducational ContentMath TutorialNakiya RimmerLearning Resource