SPSS (10): Chi-Square Test
TLDRThis video tutorial demonstrates how to perform a Chi-square test to determine if there is a statistically significant difference between two categorical variables, using gender and school type as examples. The presenter guides viewers through the process in SPSS, from setting up the crosstabs to interpreting the observed and expected values, concluding with the p-value to decide whether to reject the null hypothesis. The example concludes that there is no significant difference in the distribution of males and females attending public versus private schools.
Takeaways
- 📚 The video is a tutorial on how to perform a chi-square test to determine statistical significance in the context of two categorical variables.
- 🔍 The example used in the video involves analyzing the relationship between gender and school type (public or private) to see if there is a significant difference in the distribution.
- 📊 The chi-square test is applicable even when the categorical variables have more than two categories, but the example provided focuses on binary categories for simplicity.
- 👉 The process of conducting a chi-square test in the video involves using a statistical software, where the 'outcome' variable (school type) is placed on the columns and the 'category' variable (gender) on the rows.
- 👀 The observed values are presented in a crosstab, showing the count of individuals in each category of the variables.
- 🔢 The chi-square test calculates the expected values for each cell of the crosstab based on the assumption that there is no significant difference between the categories.
- 📈 The test compares the observed values with the expected values to determine if the differences are statistically significant.
- 📝 The video demonstrates how to run the chi-square test in a statistical software, including selecting the test and choosing options to view expected values.
- 🔑 The Pearson chi-square test is mentioned as the most common test used for this purpose.
- 📉 The significance of the test is determined by the p-value, with a value higher than 0.05 typically leading to the conclusion that there is no significant difference between the categories.
- 🚫 In the video's example, the p-value is higher than 0.05, leading to the failure to reject the null hypothesis, which states that there is no difference in the distribution of gender across public and private schools.
Q & A
What is the main topic of the video?
-The video demonstrates how to perform a chi-square test to determine if there is a statistically significant difference in the outcome based on the interaction of two categorical variables, using gender and school type as examples.
What are the two categorical variables used in the video example?
-The two categorical variables used in the example are gender (male and female) and school type (public and private).
What is the null hypothesis in the chi-square test presented in the video?
-The null hypothesis is that there is no significant difference in the distribution of males and females attending private or public schools.
What statistical test is used to analyze the categorical data in the video?
-The chi-square test is used to analyze the categorical data and determine the statistical significance of the observed differences.
How many categories can a chi-square test handle for each variable?
-A chi-square test can handle more than two categories for each variable, but in the video example, each variable has two categories.
What is the significance level used in the video to determine if the result is statistically significant?
-The significance level used in the video is 0.05. If the p-value is higher than this threshold, the null hypothesis is not rejected.
What does it mean to 'fail to reject the null hypothesis' in the context of the video?
-Failing to reject the null hypothesis means that there is not enough evidence to conclude that there is a significant difference between the groups based on the variables being tested.
What is the observed value in the context of a chi-square test?
-The observed values are the actual data collected from the sample, showing the number of individuals in each category of the variables being tested.
What are the expected values in a chi-square test, and why are they important?
-Expected values are the values that would be expected under the null hypothesis if there were no relationship between the variables. They are important for comparing with observed values to determine if the differences are statistically significant.
What is the Pearson chi-square test mentioned in the video?
-The Pearson chi-square test is a specific type of chi-square test that compares the observed frequencies in each cell of a contingency table to the frequencies that would be expected if the null hypothesis were true.
What should the viewer do if they liked the video according to the video's closing remarks?
-If the viewer liked the video, they should like, comment, share, and subscribe to the YouTube channel.
Outlines
📊 Chi-Square Test for Categorical Variables
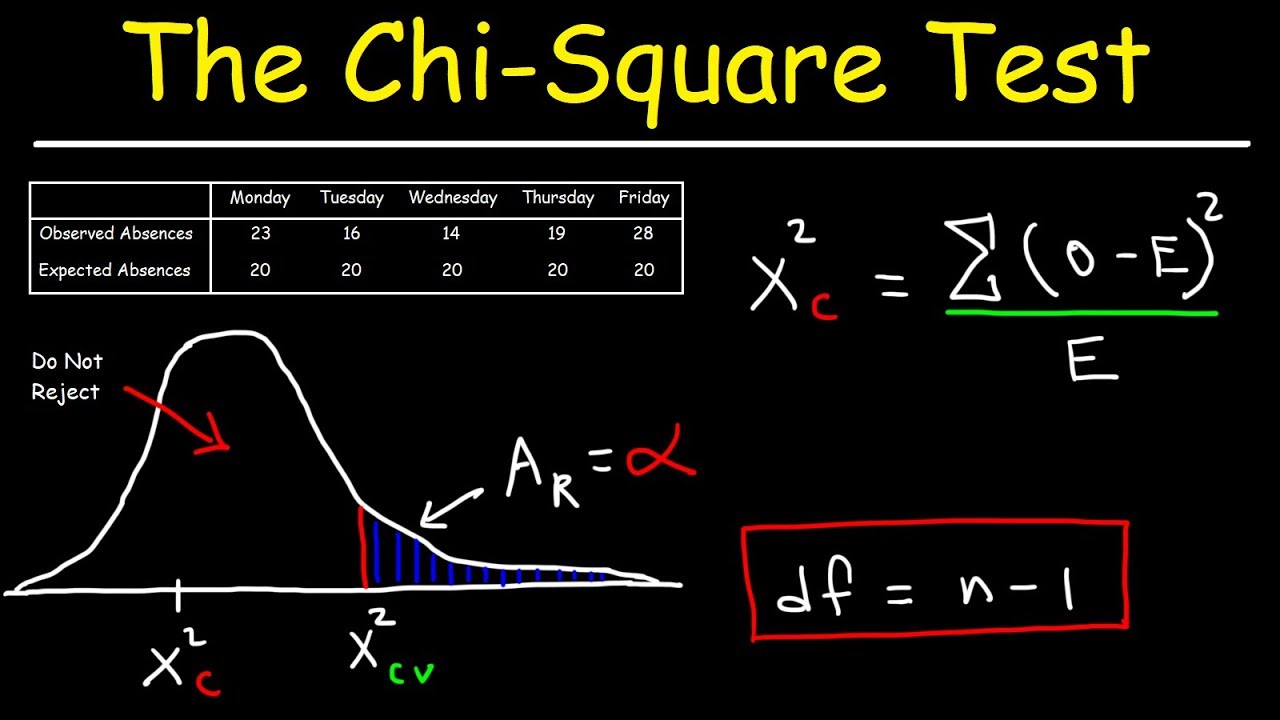
This paragraph introduces the Chi-Square test, a statistical method used to determine if there is a significant difference between two categorical variables. The example given is to examine the relationship between gender and school type (public or private). The speaker guides through the process of setting up the test in a statistical software, emphasizing the need for observed values and how to interpret the results. The test setup involves placing the outcome variable in columns and the categories in rows. The paragraph concludes with the observation of the data and the anticipation of running the Chi-Square test to find out if there is a significant difference in the distribution of genders across public and private schools.
🔍 Analyzing Chi-Square Test Results
The second paragraph delves into the analysis of the Chi-Square test results. The speaker explains how to navigate the statistical software to perform the test, including selecting the Chi-Square option and choosing to view expected values for each cell. The explanation includes a brief mention of the theory behind the test without going into depth, focusing instead on the practical application. The results are presented, showing the observed and expected values for each category. The paragraph concludes with the interpretation of the Chi-Square test's p-value, indicating that if the p-value is higher than 0.05, the null hypothesis—that there is no significant difference in the distribution of genders across school types—is accepted.
Mindmap
Keywords
💡Chi-square test
💡Categorical variables
💡Observed values
💡Expected values
💡Null hypothesis
💡Significance level (p-value)
💡Pearson chi-square
💡Cross-tabulation (crosstabs)
💡Descriptives
💡Fail to reject the null hypothesis
Highlights
Introduction to the Chi-square test for analyzing the statistical significance of differences between two categorical variables.
Explanation of the Chi-square test's application in assessing the relationship between gender and school type (public or private).
Demonstration of how to perform a Chi-square test using statistical software, starting with selecting 'Analyze' and 'Descriptives'.
Guidance on placing the outcome variable (gender) in the columns and the category variable (school type) in the rows for the Chi-square test setup.
Observation of the observed values for different groups, such as the number of males and females attending public and private schools.
Clarification that the Chi-square test can accommodate more than two categories in each variable.
Process of running the Chi-square test, including selecting 'Crosstabs' and 'Statistics'.
Instruction to check the 'Chi-square' option and request expected values for each cell in the analysis.
Explanation of how the Chi-square test works based on observed and expected values to determine significant differences.
Emphasis on the Pearson Chi-squared test as the most common method for such analysis.
Discussion of the p-value and its role in determining whether to reject the null hypothesis in the Chi-square test.
Interpretation of the results, where a p-value higher than 0.05 leads to the failure to reject the null hypothesis.
Conclusion that there is no significant difference in the gender distribution between public and private school attendees based on the Chi-square test.
Advice on the practical implications of the test results for understanding the relationship between gender and school type.
Encouragement for viewers to like, comment, share, and subscribe for more informative content.
Thank you note for watching the video and an invitation to engage with the YouTube channel.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: