You Know I'm All About that Bayes: Crash Course Statistics #24

CrashCourse

25 Jul 201812:05

EducationalLearning

32 Likes 10 Comments

TLDRThis video explains Bayesian statistics, a method of statistical inference that allows people to update their beliefs by incorporating new evidence. It uses Bayes' Theorem to calculate how the probability of something changes with new information. The video gives examples like estimating if someone is a Star Wars fan based on whether they've seen the new movie. It discusses how Bayesian analysis includes subjective prior beliefs, but claims the Bayes Factor allows people with different priors to update beliefs based on evidence. The video argues Bayesian logic matches how we naturally update beliefs, like a doctor diagnosing patients or a person judging a friend's kindness over time.

Takeaways

😀 We all have beliefs and models about how the world works that change based on new experiences and information.
👩‍🔬 Bayes' theorem allows us to calculate the probability of one event occurring given that another event has occurred.
📊 We can use Bayes' theorem to update our beliefs when we get new information.
🔢 The Bayes factor represents how much new data changes our belief about two competing hypotheses.
🤔 Bayesian statistics includes our subjective beliefs as part of the analysis.
🧠 It provides a framework for how two people can look at the same data and come to different conclusions based on their prior beliefs.
📈 The more evidence there is, the more our conclusions will be based on the evidence rather than our original beliefs.
🔭 Bayesian hypothesis testing allows us to quantify the process of updating our beliefs with new information, just like we do informally in everyday life.
👩‍⚕️ Doctors can use Bayesian logic to update the probability a patient has a certain illness based on their symptoms.
🗓 Yesterday's posterior belief becomes today's prior when updating beliefs with new evidence over time.

Q & A

What is Bayes' Theorem and how does it work?
-Bayes' Theorem tells us the probability of A given B is the probability of B given A times the probability of A, all divided by the probability of B. It allows us to update our beliefs about probabilities based on new evidence.
How did Maria use Bayes' Theorem to update her belief about whether her blind date Jordan was a Star Wars fan?
-Maria started with a prior belief that there was a 60% chance Jordan was a fan. After learning he had seen the latest movie, she calculated the Bayes Factor to determine how much to update her belief. This led to a posterior belief there was a 97% chance he was a fan.
What are some real life examples of using Bayesian inference?
-Doctors use patient symptoms to update prior beliefs about diagnoses to determine treatment. We also naturally update beliefs about friends' personalities when we observe evidence of their kindness over time.
What is subjective about Bayesian hypothesis testing?
-The prior beliefs about the probabilities of the hypotheses are subjective and depend on personal experience. Different people may start with different priors.
How can people with different prior beliefs interpret the same Bayesian analysis?
-By reporting the Bayes Factor along with the posterior odds, others can adjust the analysis based on their own prior beliefs about the hypotheses.
What happens when there is a lot of evidence relative to the prior beliefs?
-When there is sufficient evidence, it tends to overwhelm the prior beliefs. So people with very different priors may end up with similar posterior conclusions.
How does Bayesian analysis reflect how we update beliefs in real life?
-It formalizes the logical process of taking our existing beliefs, observing new evidence, and integrating the evidence to update our understanding.
What role do prior and posterior play in Bayesian inference?
-The prior is what you believed before seeing evidence. The posterior is what you believe after seeing the evidence and updating based on likelihoods.
What is the Bayes Factor in Bayesian hypothesis testing?
-The Bayes Factor represents how much the observed data changes the relative likelihood of the hypotheses. It allows updating priors.
What is a strength of the Bayesian approach compared to other statistical methods?
-It provides a framework for sequentially updating beliefs as new evidence comes in, similar to how we naturally learn in real life.

Outlines

00:00

😊 Intro to Statistics and Bayes' Theorem

This paragraph introduces statistics as a way to quantify our beliefs and models about how the world works. It then explains Bayes' Theorem, which allows us to calculate the probability of one event given that another event occurred.

05:01

😮 Example of Using Bayes' Theorem

This paragraph provides an example of using Bayes' Theorem to estimate the probability that someone with breast cancer is male, given base rates of breast cancer and being male in the general population.

10:01

🧠 Bayes' Theorem for Updating Beliefs

This paragraph explains how Bayes' Theorem can be used to update beliefs when new evidence arises, using an example of estimating if someone is a Star Wars fan based on whether they saw the latest movie. It introduces key Bayesian concepts like prior odds, likelihood, posterior odds and Bayes Factors.

😕 Subjectivity in Bayesian Statistics

This paragraph acknowledges criticism of Bayesian statistics due to the inclusion of subjective prior beliefs. It explains how reporting Bayes Factors allows readers to update beliefs based on evidence, even if they disagree with the researcher's priors.

😃 Convergence Despite Different Priors

This paragraph notes that with enough evidence, Bayesian inferences often lead people with different prior beliefs to converge on the same conclusions. It provides examples of co-workers updating beliefs on sushi safety given extensive evidence.

🤓 Bayesian Reasoning in Everyday Life

This closing paragraph relates Bayesian hypothesis testing to real-world examples like a doctor diagnosing patients or someone evaluating a friend's kindness over time. It notes that Bayesian inference aligns with how people naturally update beliefs.

Mindmap

Keywords

💡Bayes' Theorem

Bayes' Theorem is a formula for calculating conditional probabilities. It tells us the probability of A happening, given that B has occurred. This allows us to update our beliefs about A based on new evidence from B. In the video, Bayes' Theorem is used to quantify how likely it is that Maria's date Jordan is a Star Wars fan, given that he saw the latest Star Wars movie.

💡prior odds

The prior odds refer to our initial belief about something before we have new evidence. For example, Maria believed there was a 60% chance Jordan was a Star Wars fan based on her experience, before she learned he had seen the new movie. Our prior odds are our starting beliefs that can be updated.

💡posterior odds

The posterior odds are our new, updated beliefs after incorporating new evidence. For example, after Maria learned Jordan had seen the new Star Wars movie, she updated her belief about his chances of being a fan using Bayes' Theorem. Her posterior odds were higher than her prior odds.

💡Bayes Factor

The Bayes Factor represents how much the new evidence should change our belief from the prior odds to the posterior odds. It is the ratio of the probability of the evidence under two competing hypotheses. Maria used the Bayes Factor to quantify how much learning about Jordan seeing the movie should update her belief about him being a fan.

💡hypotheses

Hypotheses are the possible explanations we are testing. In Bayesian statistics, we compare two competing hypotheses given the evidence. Maria compared the hypothesis that Jordan was a Star Wars fan to the hypothesis he was not, based on the evidence of whether he had seen the latest movie.

💡subjective belief

Bayesian statistics includes our subjective, personal beliefs in the calculations through the prior odds. For example, Maria believed initially there was a 60% chance Jordan was a fan based on her experience meeting people. This subjectivity is a criticism and advantage of Bayesian methods.

💡evidence

Evidence is the new data we observe, which allows us to update our prior beliefs to posterior beliefs. For Maria, the evidence was that Jordan had seen the latest Star Wars movie, which updated her belief about whether he was a fan. Bayesian statistics provides a framework for quantifying how evidence impacts our beliefs.

💡probability

Probabilities represent the likelihood of something happening. Bayes' Theorem uses conditional probabilities to calculate the probability of one thing happening (a hypothesis being true) given that some other thing has happened (we have observed evidence).

💡update beliefs

A core concept in Bayesian statistics is updating what we currently believe based on new evidence. Our posterior beliefs are our updated conclusions after seeing new information and accounting for our prior beliefs. This reflects how we naturally learn.

💡likelihood

In Bayesian statistics, the likelihood refers to how probable the evidence is under two competing hypotheses. The ratio of these likelihoods for each hypothesis makes up the Bayes Factor that lets us update our beliefs from the prior odds to posterior odds.

Highlights

Bayes' Theorem tells us the probability of A given B is the probability of B given A times the probability of A, all divided by the probability of B.

Bayes' Theorem allows you to update your beliefs based on new information.

We start with some idea or belief about how something works, and then test hypotheses using Bayesian statistics.

The ratio of the probability of our information under one hypothesis compared to another is called a Bayes' Factor.

In Bayesian statistics, prior, likelihood, and posterior refer to beliefs before evidence, how evidence changes beliefs, and updated beliefs.

Bayesian hypothesis testing includes subjective beliefs, but the Bayes Factor allows anyone to update their beliefs with evidence.

Often when there's sufficient evidence, two people with different prior odds will come to the same conclusion.

Bayesian methods explain why two people can see the same evidence and reach different conclusions.

Bayesian inference allows you to continuously update your beliefs with new evidence over time.

Bayesian hypothesis testing quantifies how we logically incorporate new events into our worldview.

Doctors use Bayesian logic to update odds of diagnoses given patient symptoms.

You update your belief in a caring friend by seeing continuous evidence of their kindness over time.

In Bayesian statistics, yesterday's posterior belief becomes today's prior to be updated again.

Bayes' theorem calculates the probability of one hypothesis given observed data.

Bayesian hypothesis testing compares the ratio of two hypotheses given observed data.

Transcripts

Browse More Related Video

Bayes in Science and Everyday Life: Crash Course Statistics #25

Probability Part 2: Updating Your Beliefs with Bayes: Crash Course Statistics #14

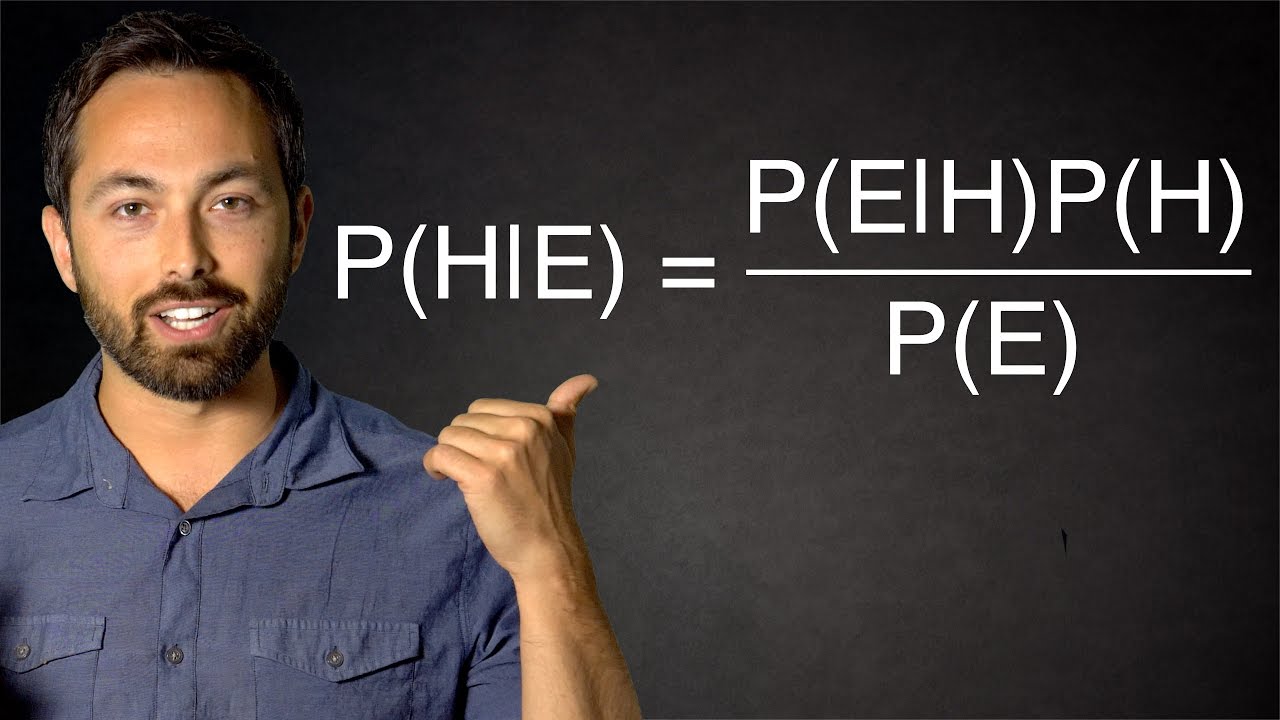
The Bayesian Trap

Are you Bayesian or Frequentist?

Bayes theorem, the geometry of changing beliefs

10. Saturday Panel: Conceptions of Empirical Success Conference