Test of Independence Using Chi-Square Distribution

The Organic Chemistry Tutor
24 Nov 201913:03
EducationalLearning
32 Likes 10 Comments

TLDRThe script analyzes whether the average number of hours high school students spend studying is independent of their grade level. It steps through constructing a contingency table showing the observed data, determining the expected values to test for independence, formulating the null and alternative hypotheses, calculating degrees of freedom, finding the critical value from a chi-square distribution table, computing the test statistic, and comparing it to the critical value in order to make a decision. Since the test statistic falls in the rejection region, there is evidence to reject the null hypothesis and conclude that study time depends on student type, specifically that seniors study less than freshmen.

Takeaways
  • 😀 The transcript discusses a statistical analysis using a chi-square test to determine if the average number of study hours is dependent on the type of high school student.
  • 📊 A contingency table is constructed showing the number of freshman and senior students studying different hourly ranges.
  • 🤔 The null hypothesis is that study hours are independent of student type.
  • 📐 Degrees of freedom are calculated to be 2 for the analysis.
  • 🔢 Expected values are computed for the contingency table cells.
  • ☑️ The calculated chi-square statistic is compared to the critical value.
  • ❗ The calculated value falls in the rejection region, so the null hypothesis is rejected.
  • 👩‍🎓 There is evidence that seniors spend less time studying than freshmen.
  • 😟 This could be indicative of "senioritis" among the senior students.
  • 📋 The analysis demonstrates using chi-square tests for independence with contingency tables.
Q & A

  • What are the two hypotheses being tested in this analysis?

    -The null hypothesis is that the average number of hours studied is independent of the type of student. The alternative hypothesis is that the average number of hours studied depends on the type of student.

  • How many degrees of freedom are there for the chi-square test?

    -There are 2 degrees of freedom, calculated as (number of rows - 1) x (number of columns - 1) = (2-1) x (3-1) = 1 x 2 = 2.

  • What is the critical value for the chi-square test?

    -With 2 degrees of freedom and α = 0.05, the critical chi-square value is 5.99.

  • What is the calculated chi-square statistic?

    -The calculated chi-square statistic is 32.3.

  • What can we conclude from the chi-square test result?

    -Since the calculated chi-square value of 32.3 is greater than the critical value of 5.99, we reject the null hypothesis. There is evidence that the average number of hours studied depends on the type of student.

  • Which group studies the most hours per day on average?

    -Freshmen study the most hours per day on average. The data shows freshmen study 2-4 hours per day more frequently than seniors.

  • How are the expected frequencies calculated?

    -The expected frequencies are calculated by taking the row total × column total / total n. For example, the expected frequency for freshmen studying 2-4 hours is 310 × 252 / 630 = 124.

  • What assumptions need to be met to use the chi-square test?

    -The chi-square test requires that the expected frequencies should be greater than 5 in at least 80% of the cells, and no cell should have an expected frequency of less than 1.

  • What causes the senioritis mentioned at the end of the transcript?

    -Senioritis refers to a decrease in motivation that some students experience their senior year of high school as they look ahead to graduating and moving on from high school.

  • What additional data could help explain the difference in study hours between freshmen and seniors?

    -Data on the difficulty or workload of classes, involvement in extracurricular activities, job/family responsibilities, plans after graduation, and overall motivation levels could help further explain the difference in study hours.

Outlines
00:00
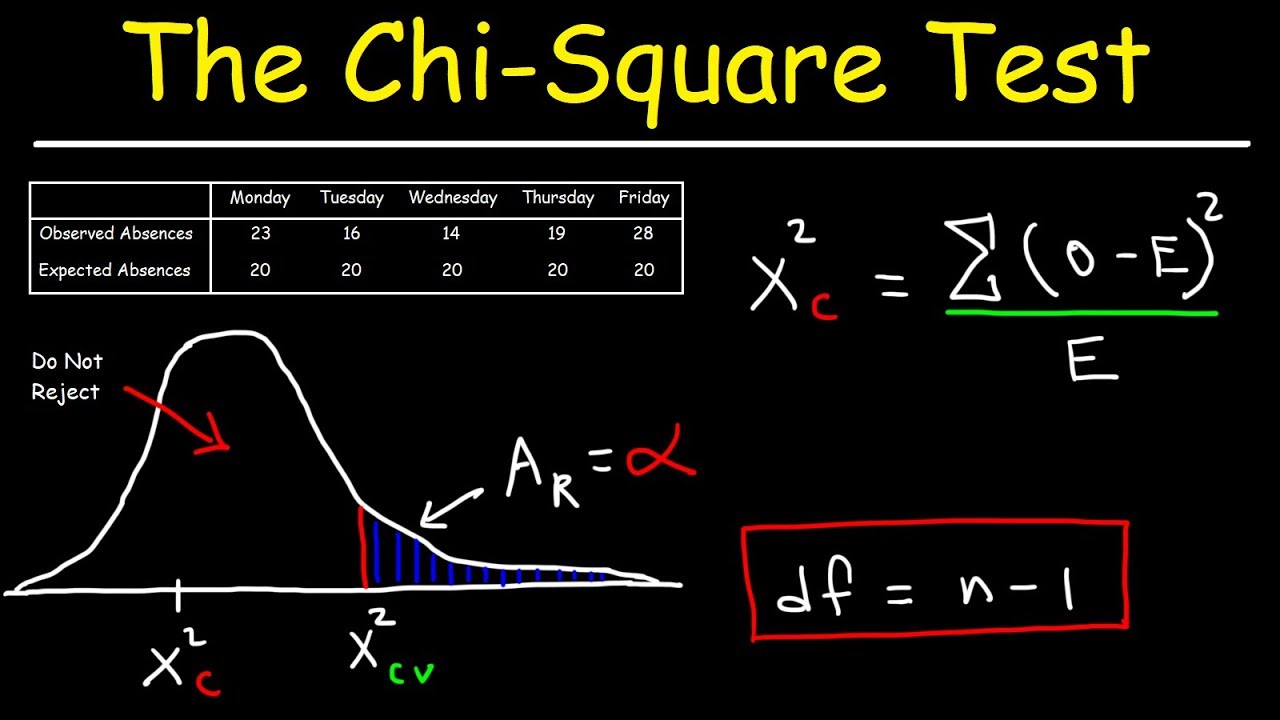
📊 Building a Contingency Table for a Chi-Square Test

This paragraph discusses creating a contingency table to perform a chi-square test of independence to determine if the average number of study hours depends on the type of high school student. It calculates the totals for the rows and columns in the table, states the null and alternative hypotheses, calculates the degrees of freedom, and explains the test procedure using the chi-square distribution.

05:02
📉 Calculating Expected Values for the Chi-Square Test

This paragraph shows the calculation of the expected values for each cell in the contingency table using the provided formula. It calculates and rounds the expected values and verifies the row and column totals match the original table.

10:05
📈 Calculating and Interpreting the Chi-Square Statistic

This paragraph calculates the chi-square statistic using the observed and expected values. It compares the calculated value to the critical value, determines the result falls in the rejection region, rejects the null hypothesis, and concludes there is evidence that average study hours depends on student type, noting seniors spend less time.

Mindmap
Keywords
💡Contingency Table
A contingency table is a type of table in a matrix format that displays the frequency distribution of the variables. It's crucial for analyzing the relationship between two categorical variables. In the video, a contingency table is used to organize the average number of hours students spend studying per day by their classification (freshmen or seniors) and the time spent studying. This table is foundational for conducting the chi-square test of independence, which assesses whether there is a significant association between the type of student and their study hours.
💡Chi-Square Test of Independence
The chi-square test of independence is a statistical test used to determine whether there is a significant association between two categorical variables. It's based on comparing observed frequencies to expected frequencies. The video script walks through conducting this test to explore if the average number of study hours is dependent on the type of student (freshman or senior), using the data organized in a contingency table. The chi-square distribution and critical values are used to decide whether to reject the null hypothesis.
💡Null Hypothesis
The null hypothesis represents a statement of no effect or no difference, used as a default assumption that there is no relationship between two measured phenomena. In the context of the video, the null hypothesis posits that the average number of study hours is independent of the student type. This hypothesis is what the chi-square test of independence seeks to test, determining whether to accept or reject it based on the statistical evidence.
💡Alternative Hypothesis
The alternative hypothesis is a statement that suggests a potential effect, difference, or association that opposes the null hypothesis. In the script, the alternative hypothesis proposes that the average number of study hours is dependent on the student type. The chi-square test aims to find enough evidence to support the alternative hypothesis, indicating a significant relationship between student type and study hours.
💡Degrees of Freedom
Degrees of freedom are a statistical concept used to determine the number of independent pieces of information in a dataset that are free to vary when estimating a parameter. In the video, the calculation of degrees of freedom is based on the formula '(number of rows - 1) x (number of columns - 1)', resulting in two degrees of freedom for the chi-square test. This is crucial for determining the appropriate critical value from the chi-square distribution table.
💡Critical Value
The critical value in statistics is a point on the distribution that is compared with the test statistic to decide whether to reject the null hypothesis. The script explains that the critical value for the chi-square test, with two degrees of freedom and a significance level of 0.05, is 5.99. If the calculated chi-square value exceeds this critical value, the null hypothesis is rejected, indicating a significant association between variables.
💡Expected Values
Expected values in the context of the chi-square test refer to the theoretical frequencies that would be observed if there were no association between the categorical variables. The video details calculating expected values by multiplying the row and column totals of the contingency table and dividing by the grand total. These expected values are essential for comparing against the observed values to compute the chi-square statistic.
💡Calculated Chi-Square Value
The calculated chi-square value is the result of the chi-square test formula, which sums the squared differences between observed and expected values, divided by the expected values. In the script, this calculation yields a chi-square value of 32.3, indicating the test statistic used to evaluate the strength of the association between student type and study hours against the critical value.
💡Rejection Region
The rejection region in hypothesis testing is a range of values for which the null hypothesis is rejected in favor of the alternative hypothesis. It is determined by the critical value and the significance level. The video explains that with a critical value of 5.99 and a calculated chi-square value of 32.3, the result falls into the rejection region, leading to the rejection of the null hypothesis and suggesting a dependency of study hours on student type.
💡Significance Level (Alpha)
The significance level, denoted as alpha, is the probability of rejecting the null hypothesis when it is true, essentially measuring the risk of a Type I error. In the script, a significance level of 0.05 is used, indicating a 5% risk of incorrectly rejecting the null hypothesis. It defines the threshold for the critical value in the chi-square test and helps determine the rejection region for the hypothesis test.
Highlights

Completes a contingency table to analyze the average number of hours students spend studying

States the null and alternative hypotheses for testing if study hours depends on student type

Calculates 2 degrees of freedom for the chi-square test

Explains using a right-tailed chi-square test with α = 0.05 significance level

Determines critical chi-square value from table is 5.99 with 2 degrees of freedom

Calculates expected values for each cell in contingency table

Sums differences between observed and expected values squared over expected values to get chi-square statistic

Obtains chi-square test statistic value of 32.3

Compares test statistic to critical value and rejects null hypothesis since it falls in rejection region

Concludes there is evidence that average study hours depends on student type

Seniors spend much less time studying than freshmen

Perhaps seniors have "senioritis" with less motivation to study

Contingency table analysis using chi-square test of independence

Right-tailed test critical region reflects α = 0.05 significance level

Test statistic outside critical value region leads to null hypothesis rejection

Transcripts

Browse More Related Video

Chi Square Test

Chi Square Distribution Test of a Single Variance or Standard Deviation

8.1.4 Basics of Hypothesis Testing - The Critical Value Method for a Population Proportion

Test Statistic For Means and Population Proportions

Hypothesis Testing With Two Proportions

Math 119 Chap 8 part 3

Rate This

5.0 / 5 (0 votes)

Thanks for rating: