LSD; Least Significant Difference; Post Hoc Test of ANOVA; Comparison of Means (Part B)

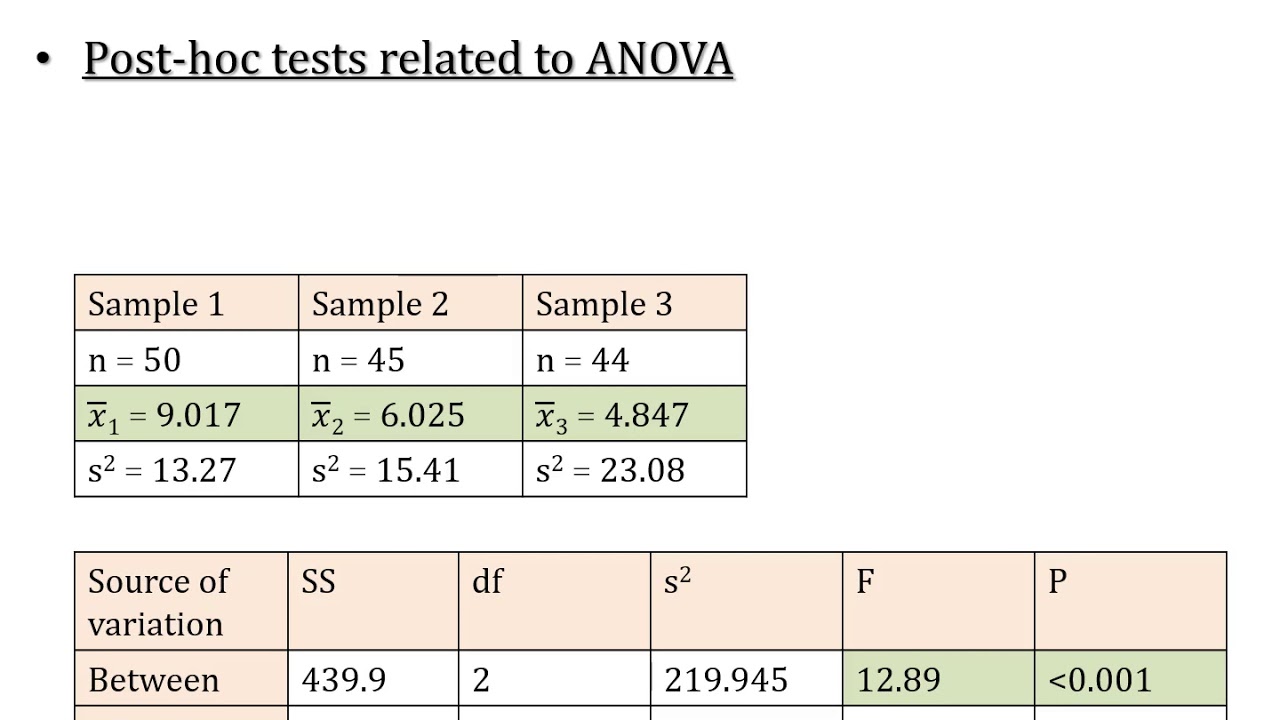
This paragraph introduces the concept of post-hoc tests, specifically focusing on Fisher's Least Significant Difference (LSD) test, developed in 1935. The LSD is a method used to determine which means are significantly different from each other after a significant F-test in ANOVA. The formula for LSD is explained, involving the t-value from the t-distribution table, degrees of freedom (v), and the desired level of significance (alpha). The process of conducting pairwise comparisons and the conditions under which the test is applied are discussed, including the use of variance within from the ANOVA table and the number of observations (n). The paragraph also outlines the stepwise approach to conducting LSD tests at different significance levels, starting with 0.05, followed by 0.01 and 0.001, with each step only testing pairs that were significant in the previous step.

The paragraph details the process of calculating the Least Significant Difference (LSD) at a 0.05 significance level using a given formula and dataset. It explains how to use the t-value, variance within from the ANOVA table, and the number of observations to compute the LSD value for pairwise comparisons of sample means. The calculated LSD value is then used to compare mean differences to determine if they are significant or non-significant. The paragraph also discusses the next steps of conducting the LSD test at 0.01 and 0.001 significance levels, emphasizing that these tests are only performed on pairs that were found significant at the previous level.

This section describes the continuation of the LSD test at the 0.01 significance level for the pairs that were found significant at the 0.05 level. It explains the re-calculation of the LSD using a different t-value for the 0.01 significance level and the same variance within from the ANOVA table. The comparison of mean differences with the newly calculated LSD value is discussed, with the result indicating which pairs remain significant at the 0.01 level. The paragraph also sets the stage for further analysis at the 0.001 significance level for the pairs that are significant at 0.01.

The paragraph presents the final stage of the LSD analysis at the 0.001 significance level, focusing only on the pairs that were significant at the 0.01 level. It explains the calculation of the LSD using a t-value for the 0.001 significance level and the variance within from the ANOVA table. The comparison of mean differences with the LSD value at this level is discussed, and the results show which pairs are very highly significant. The paragraph concludes with the presentation of the results in a table format, indicating the significance levels of the differences between sample means.

This paragraph discusses the application of the LSD test to determine significant differences in the mean autolet diameter of fish exposed to different temperatures. It outlines the process of creating a table for pairwise differences in means and calculating the LSD for each pair at the 0.05 significance level, taking into account the different number of observations in each sample. The results of the pairwise comparisons are summarized, highlighting which pairs are significant and which are not.

The paragraph describes the process of conducting the LSD test when the number of observations in each sample is different. It explains how to calculate the LSD for each pair of samples at the 0.05 significance level, using the appropriate t-value, variance within, and number of observations for each specific pair. The calculated LSD values are then used to compare the mean differences and determine their significance. The paragraph also discusses the continuation of the test at the 0.01 significance level for the pairs that were found significant at the 0.05 level.

This paragraph details the continuation of the LSD test at the 0.01 and 0.001 significance levels for the pairs that were found significant at the 0.05 level. It explains the re-calculation of the LSD using the appropriate t-values for both significance levels and the comparison of mean differences with these new LSD values. The results indicate which pairs are highly significant at the 0.01 level and very highly significant at the 0.001 level. The paragraph concludes with the presentation of the final LSD table, summarizing the significance of the differences between sample means.

The final paragraph provides a summary of the LSD exercises conducted for the day, highlighting the methodology used for both exercises involving different numbers of samples and observations. It emphasizes the importance of the LSD test as a post-hoc analysis tool following ANOVA to identify which specific mean pairs are significantly different. The paragraph concludes by reiterating the results of the exercises and the general approach to performing and interpreting the LSD test.