Math 119 Chapter 4 part 2
TLDRThis educational video script delves into the concepts of probability, focusing on the multiplication rule for independent and dependent events. It illustrates these principles with examples like drawing marbles from a bag and flipping coins, and explains how to calculate the likelihood of sequential events. The script further explores real-world applications, such as the impact of attending a review session on exam pass rates, and introduces the use of tree diagrams for visualizing probabilities. It concludes with practical problems involving tire selection and Skittles to reinforce the concepts taught.
Takeaways
- 📚 The video discusses the multiplication rule in probability, emphasizing the difference between dependent and independent events.
- 🎲 The script uses a marble example to illustrate how the probability of drawing a second yellow marble is affected by the first draw, demonstrating dependent events.
- 🔄 It explains that if you put the first marble back, the probability of drawing a yellow remains the same for the second draw, showing an independent event.
- 🏠 The video gives a real-world example relating graduating from college (event A) to owning a home (event B), suggesting that these are dependent events.
- 🤔 The importance of understanding whether events are dependent or independent is stressed, as it affects how probabilities are calculated.
- 🔢 The script provides mathematical formulas and examples to calculate the probability of multiple events occurring, such as rolling a die and flipping a coin.
- 🧩 The concept of 'at least one' in probability is introduced, using the example of finding the probability that at least one person in a group has type A blood.
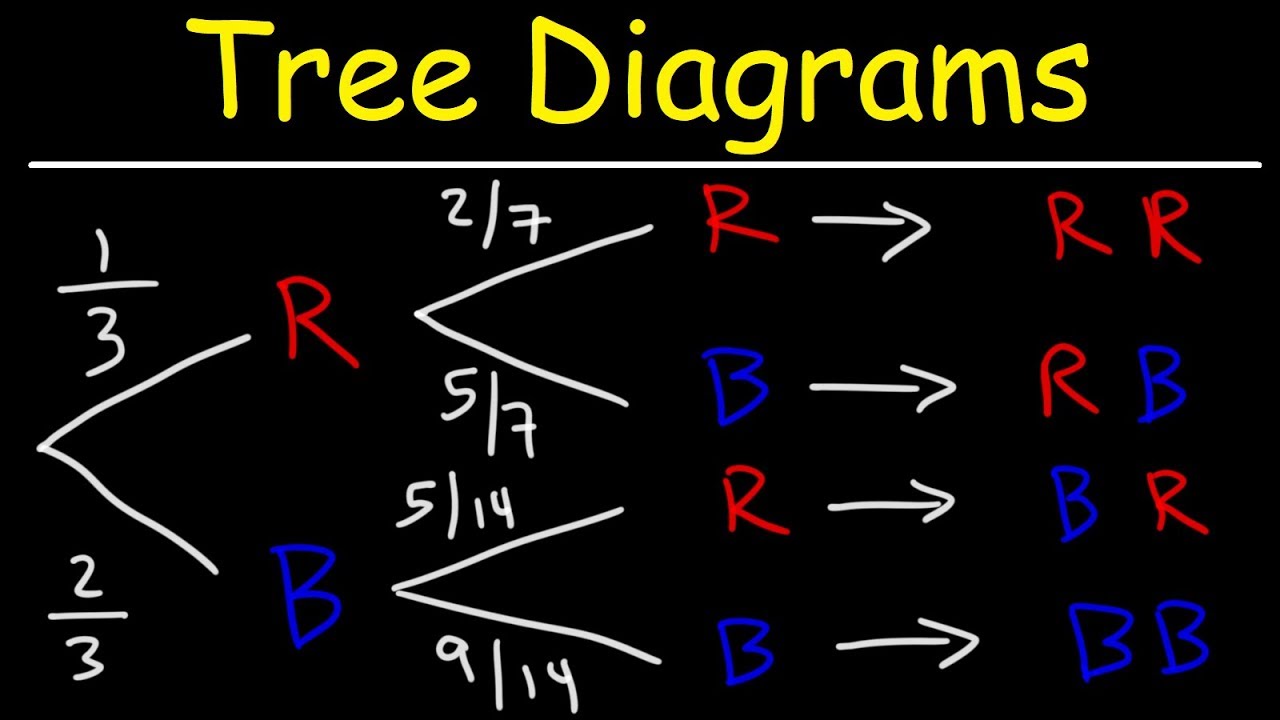
- 📉 The video uses a tree diagram to visually represent probabilities of different outcomes, like passing an exam based on attending a review session or not.
- 🤷♂️ The script mentions Bayes's rule in the context of finding reverse conditional probabilities, though it does not delve deeply into the topic.
- 🛒 A tire purchasing example highlights the calculation of probabilities in a dependent scenario, where the selection of one item affects the next.
- 🍭 The video concludes with a Skittles example, calculating the probability of selecting a certain number of a specific color with and without replacement.
Q & A
What is the main topic of the second video in chapter four?
-The main topic of the second video in chapter four is the multiplication rule in probability, which involves calculating the probability of two events occurring in sequence.
What is the basic concept behind the multiplication rule for dependent events?
-The basic concept behind the multiplication rule for dependent events is that the occurrence of the first event affects the probability of the second event. This is represented mathematically as P(A and B) = P(A) * P(B|A), where P(B|A) is the probability of B given A.
Can you provide an example of a dependent event from the script?
-An example of a dependent event from the script is drawing marbles from a bag. If you draw a yellow marble on the first draw, it affects the probability of drawing another yellow marble on the second draw because one marble has been removed from the bag.
What is the difference between independent and dependent events?
-Independent events are those where the occurrence of one event does not affect the probability of the other event. In contrast, dependent events are those where the occurrence of the first event influences the probability of the second event.
How does the probability of drawing a second yellow marble change if the first marble drawn is not replaced?
-If the first yellow marble drawn is not replaced, the probability of drawing a second yellow marble decreases because there is one less yellow marble and one less marble overall in the bag.
What is the probability of graduating from college (Event A) affecting the probability of owning a home (Event B)?
-The script suggests that graduating from college (Event A) does affect the probability of owning a home (Event B), as a college degree may improve job prospects and financial stability, which can influence the ability to purchase a home.
What is the formula for calculating the probability of two independent events both occurring?
-The formula for calculating the probability of two independent events both occurring is P(A and B) = P(A) * P(B), where P(A) is the probability of event A and P(B) is the probability of event B.
How does the script illustrate the concept of independent events with the example of tossing a coin?
-The script illustrates the concept of independent events by showing that the outcome of one coin toss does not affect the outcome of the next. The probability of getting heads on the second toss remains 1/2, regardless of the result of the first toss.
What is the concept of 'at least one' in the context of probability problems?
-The concept of 'at least one' in probability refers to the scenario where at least one of the specified events occurs. It can be calculated by considering all the possible scenarios where the event happens at least once or by using the complement rule, which is 1 minus the probability of the event not happening at all.
How does the script explain the use of a tree diagram in probability?
-The script explains the use of a tree diagram as an extension of the general multiplication rule. It helps visualize all possible outcomes of an event and allows for the calculation of probabilities by breaking down the problem into branches that represent each possible outcome.
Outlines
🔢 Multiplication Rule and Dependent Events
The video begins by introducing the multiplication rule for calculating the probability of two events occurring in sequence, emphasizing the difference between dependent and independent events. A marble drawing example illustrates how the outcome of the first event can affect the probability of the second. The script also discusses the impact of graduating from college on the likelihood of owning a home, using real-life scenarios to clarify the concept of dependent events.
🎲 Independent Events and Probability Calculations
This section delves into independent events, using the example of tossing a coin and rolling a die to explain how probabilities are calculated when the outcome of one event does not influence another. The script provides formulas and examples to demonstrate how to find the probability of multiple independent events occurring simultaneously, such as the coin landing on tails and the die showing a four.
🧬 Blood Types and Probabilities of Independent Events
The script explores the concept of treating large populations as if they were independent for the sake of simplicity, using the distribution of blood types in the U.S. population as an example. It explains how to calculate the probability that two randomly selected individuals both have type O blood, despite the technically dependent nature of drawing from a finite population.
🃏 Card Drawing and Conditional Probability
The video introduces a card drawing scenario to illustrate conditional probability, explaining how to calculate the likelihood of drawing an ace and then a jack from a standard deck of cards. The example demonstrates the use of dependent events in probability calculations, where the removal of a card affects the probabilities of subsequent draws.
📚 Final Review Sessions and Exam Pass Rates
This part of the script discusses the use of a probability tree to determine the likelihood of students passing a final exam based on whether they attended a review session. The tree diagram is used to visualize the different outcomes and their associated probabilities, leading to the calculation of the overall pass rate and the probability of attending the session given that a student passed the exam.
🛒 Tire Purchasing and Dependent Event Probabilities
The script presents a scenario where tires are purchased without replacement from a salvage lot, explaining how to calculate the probability of buying two damage-free tires. It emphasizes the importance of adjusting probabilities for dependent events, where the selection of one item affects the likelihood of subsequent selections.
🍭 Skittles Selection with Replacement and Without
The video concludes with a colorful example of selecting Skittles from a bag, comparing the probabilities of drawing green candies with and without replacement. This highlights the difference between independent and dependent events in probability calculations, showing how the same initial conditions can lead to different outcomes based on whether items are replaced after selection.
🟪 Probability of Selecting Purple Skittles
In the final part of the script, the focus is on calculating the probability of selecting at least one purple Skittle without replacement. The example uses the complement rule to simplify the calculation, demonstrating a strategic approach to probability problems involving 'at least one' outcomes by subtracting the probability of no purples from one.
Mindmap
Keywords
💡Multiplication Rule
💡Dependent Events
💡Independent Events
💡Conditional Probability
💡Bayes's Rule
💡Tree Diagram
💡Sampling Without Replacement
💡Complement of an Event
💡Skittles Problem
💡At Least One
Highlights
Introduction to the multiplication rule in probability theory, emphasizing the importance of understanding whether events are dependent or independent.
Explanation of how the probability of two events, A and B, occurring is calculated by multiplying their individual probabilities if they are independent.
Illustration of dependent events using the example of drawing marbles from a bag, where the outcome of one draw affects the next.
Clarification on the difference between dependent and independent events with a clear example of drawing marbles with and without replacement.
Discussion on the impact of graduating from college (event A) on the probability of owning a home (event B), as an example of dependent events.
Use of a coin toss and dice roll to demonstrate the calculation of probabilities for independent events.
The American Red Cross blood type statistics used to calculate the probability of selecting two individuals with type O blood.
Application of the multiplication rule to find the probability of drawing a specific sequence of cards, like an Ace and then a Jack, in a deck.
Introduction to tree diagrams as a method to visualize and calculate probabilities of multiple dependent events.
Example of using a tree diagram to determine the probability of passing an exam based on attending a review session.
Calculation of reverse conditional probability using the total probability of an event to find the likelihood of a related event.
Explanation of sampling with and without replacement, and how it affects the probability calculations.
Probability calculation for selecting tires from a batch where some are damaged and others are not, considering the impact of removing tires from the selection pool.
Use of a bag of Skittles to illustrate the probability of drawing a certain number of a specific color with and without replacement.
Strategy for calculating the probability of at least one event occurring by using the complement of the probability of none of the event occurring.
Final thoughts and invitation for students to ask questions during office hours, emphasizing the complexity of conditional probability.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: