AP Stats Test Quick Review: Probability
TLDRThis video script covers key concepts in probability for AP Statistics, focusing on understanding probability as long-run frequency, addition rule, conditional probability, multiplication of independent events, and probability with the normal model. It emphasizes the importance of distinguishing between mutually exclusive and independent events, using Venn diagrams and tree diagrams for clarity, and applying these concepts to solve problems.
Takeaways
- 📚 The video is a review of probability for the AP Statistics test, focusing on five key concepts and noting a separate video for the binomial model.
- 🔢 Probability is defined as the long-run relative frequency of an event, emphasizing the Law of Large Numbers and the difference between short-run and long-run frequencies.
- 🎯 The addition rule for probability, P(A or B) = P(A) + P(B) - P(A and B), is highlighted as crucial, including the concept of mutually exclusive events where P(A and B) = 0.
- 🤝 The difference between independent and dependent events is discussed, with the formula for independent events P(A and B) = P(A) * P(B) being correctly applied only when events are explicitly stated as independent.
- 🚫 A key point is made that mutually exclusive events cannot be independent, which is a unidirectional statement.
- 📈 Conditional probability is introduced with the formula P(A given B) = P(A and B) / P(B), and the importance of understanding the impact of one event on another is emphasized.
- 📊 Two-way tables are presented as useful tools for probability problems, allowing for straightforward calculations of probabilities based on given data.
- 🌳 Tree diagrams are used to solve conditional probability problems, such as the likelihood of a dog having heartworm given a positive test result.
- 🎲 Multiplying probabilities is explained for multiple independent events, with the example of rolling dice, and conditional probability for dependent events, such as selecting students from a group.
- 👶 An example of building a probability model for selecting a girl from a group of students is given, illustrating the use of conditional probability for each selection.
- 📘 The video concludes with a reminder that probability related to the normal model requires understanding of mean, standard deviation, and the use of normalcdf on calculators.
Q & A
What is the definition of probability as described in the video?
-Probability is defined as the long-run relative frequency of an event, which is how often an event occurs after many trials. It is based on the Law of Large Numbers, which states that the true probability of an event will only reveal itself after a large number of trials.
What does the Law of Large Numbers imply about the probability of an event?
-The Law of Large Numbers implies that the true probability of an event will only become apparent after a large number of trials. In the short run, any outcome is possible, but as the number of trials increases, the observed frequency of the event will converge to its true probability.
What is the addition rule for probability and why is it important?
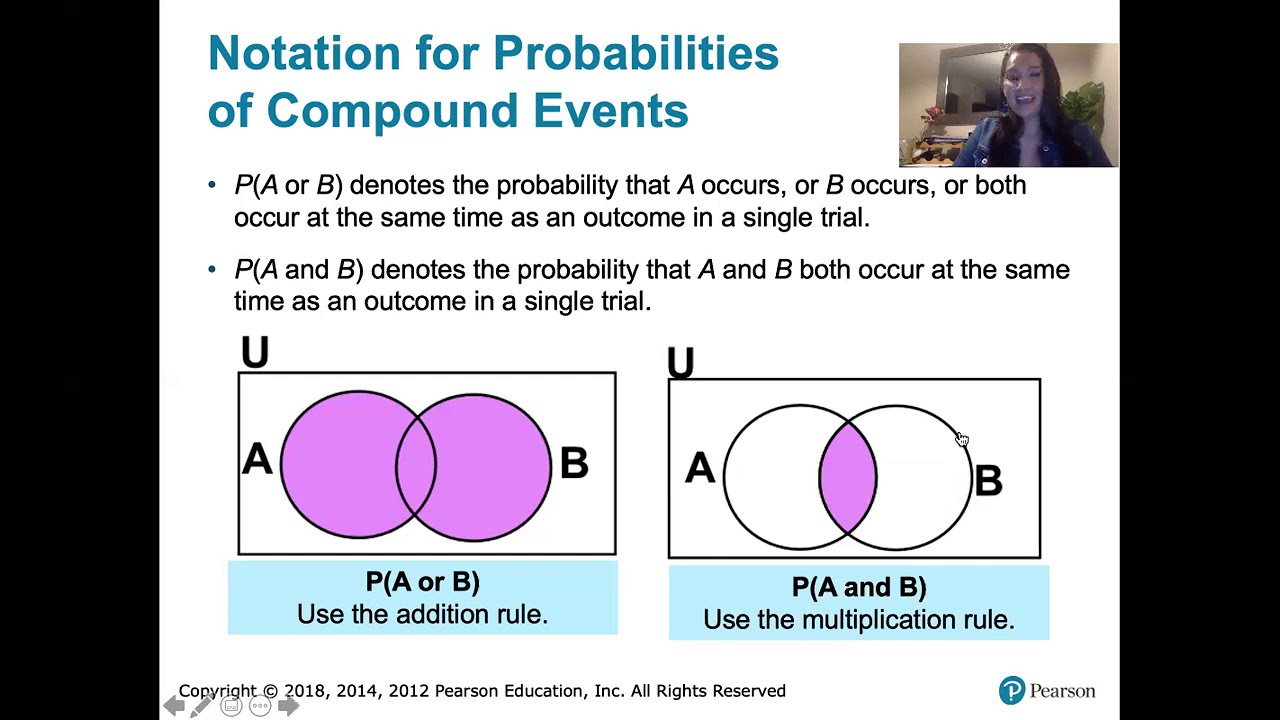
-The addition rule for probability is a fundamental principle stating that the probability of A or B occurring is equal to the probability of A plus the probability of B minus the probability of A and B. It is important because it helps to avoid double-counting the overlap between events A and B when calculating the probability of either event occurring.
What is the difference between mutually exclusive and independent events in terms of probability?
-Mutually exclusive events cannot occur at the same time, meaning the probability of both events happening together is zero. Independent events, on the other hand, do not affect each other's probability of occurrence. If two events are mutually exclusive, they cannot be independent.
How is conditional probability different from the probability of independent events?
-Conditional probability refers to the probability of an event occurring given that another event has already occurred. It is calculated by dividing the probability of both events occurring by the probability of the condition. In contrast, the probability of independent events is simply the product of their individual probabilities, as the occurrence of one does not affect the other.
What is the correct formula to use when calculating the probability of A or B if the events are mutually exclusive?
-If events A and B are mutually exclusive, the correct formula to use is P(A or B) = P(A) + P(B), since the probability of A and B occurring together is zero, and there is no need to subtract it.
How can a two-way table be used to calculate probabilities in a study?
-A two-way table can be used to calculate probabilities by looking at the frequency of outcomes in different categories. To find the probability of a particular outcome, you divide the number of occurrences of that outcome by the total number of observations in the study.
What is the probability of selecting a college graduate from a group of 2500 people, according to the two-way table in the video?
-The probability of selecting a college graduate is calculated by dividing the number of college graduates (693) by the total number of people (2500), which results in a probability of 0.2772 or 27.72%.
How can a tree diagram be used to solve probability problems involving conditional statements?
-A tree diagram can be used to visualize the different outcomes of events based on given conditions. By following the branches of the tree, you can calculate the probability of each outcome by multiplying the probabilities along the path to that outcome.
What is the probability of getting a positive test result for heartworm in dogs, given the test's accuracy rates in the video?
-The probability of getting a positive test result for heartworm is calculated by adding the probability of a dog with heartworm testing positive (0.02 * 0.95) to the probability of a dog without heartworm testing positive (0.98 * 0.15), which equals 0.166.
How can you determine if two events are independent using a two-way table?
-To determine if two events are independent, you can check if the probability of one event occurring is the same regardless of whether the other event occurs. If the probability of being a college graduate is the same for those who get news from the internet and those who don't, then the events are independent.
What is the probability of selecting a girl on the first try from a group of 7 students consisting of 4 boys and 3 girls?
-The probability of selecting a girl on the first try is the number of girls (3) divided by the total number of students (7), which is 3/7.
How can you calculate the probability of selecting all boys in a sequence of 4 picks from a group of 7 students with 4 boys and 3 girls?
-To calculate this probability, you multiply the probability of picking a boy each time: (4/7) * (3/6) * (2/5) * (1/4).
What is a normalcdf and how is it used in probability problems related to the normal model?
-A normalcdf is a function on calculators that computes the cumulative probability for a normal distribution given a mean, standard deviation, and a z-score. It is used to find probabilities in problems that involve the normal model by inputting the necessary values and using the function to get the probability.
Outlines
📚 Introduction to Probability Concepts
This paragraph introduces the concept of probability in the context of the AP Statistics test. It emphasizes the importance of understanding probability as the long-run relative frequency of an event and clarifies misconceptions about what a 50% chance means in practice. The paragraph also introduces five key areas of probability that will be covered, including the binomial model, which will be discussed in a separate video. The law of large numbers is mentioned to explain how true probabilities are revealed over many trials, and the concept of 'or' in probability is introduced, explaining the addition rule for calculating the probability of either event A or event B occurring.
🔍 Understanding 'Or' and 'And' in Probability
The paragraph delves into the addition rule for calculating the probability of 'A or B', explaining the importance of considering both mutually exclusive events and independent events. The concept of mutually exclusive events, where A and B cannot occur at the same time, is contrasted with independent events, where the occurrence of A does not affect the probability of B. The paragraph also highlights a common mistake made in calculating the probability of 'A and B', especially when events are not independent, and clarifies the correct approach using the multiplication rule for independent events.
📉 Probabilities with Two-Way Tables and Conditional Probability
This section discusses the use of two-way tables for analyzing probabilities, particularly in the context of the AP Statistics test. It provides an example of a two-way table involving education levels and news sources, demonstrating how to calculate probabilities for various scenarios. The paragraph also introduces conditional probability, explained with the formula P(A|B), and emphasizes the importance of understanding the impact of one event on another. The use of tree diagrams for visualizing conditional probabilities is also mentioned.
🤝 The Relationship Between Mutually Exclusive and Independent Events
The paragraph explores the relationship between mutually exclusive and independent events, stating that if two events are mutually exclusive, they cannot be independent. This is illustrated with the example of getting an A or a B on a test, where the occurrence of one event makes the other impossible. The concept is further clarified through the use of a Venn diagram, and the paragraph concludes with a worked example calculating the probability of A or B given different scenarios of independence and mutual exclusivity.
📈 Conditional Probability and Its Application
This paragraph focuses on conditional probability, using a tree diagram to illustrate the concept. It discusses a hypothetical situation involving a test for heartworm in dogs, explaining how to calculate the probability of a dog having heartworm given a positive test result. The importance of considering the base rate of the condition (heartworm in this case) and the accuracy of the test is highlighted, emphasizing the difference between a true positive and a false positive result.
🎲 Multiplying Probabilities for Multiple Independent Events
The paragraph discusses the process of multiplying probabilities when dealing with multiple independent events, such as rolling a die. It emphasizes that the outcome of one event does not affect the probability of another, and provides an example of calculating the probability of rolling four fives in a row. The concept is extended to other scenarios, such as selecting students from a classroom, and the importance of considering conditional probabilities when events are not independent is also mentioned.
📊 Probability in the Context of the Normal Distribution
The final paragraph touches on the application of probability in the context of the normal distribution, particularly in relation to the AP Statistics test. It advises that problems involving the normal model will require knowledge of the mean and standard deviation and suggests using a normal CDF (cumulative distribution function) calculator to find probabilities. The paragraph also reminds viewers of the importance of adjusting the standard deviation for sample means or proportions based on the sample size.
Mindmap
Keywords
💡Probability
💡Addition Rule
💡Mutually Exclusive Events
💡Independent Events
💡Conditional Probability
💡Two-Way Table
💡Normal Model
💡Binomial Model
💡Tree Diagram
💡Law of Large Numbers
Highlights
Probability is defined as the long-run relative frequency of an event.
The Law of Large Numbers states that the true probability of an event will reveal itself after a large number of trials.
Understanding the difference between short-run and long-run probabilities, exemplified by coin tosses.
The addition rule for probability, including the importance of avoiding double-counting of overlapping events.
Mutually exclusive events cannot occur at the same time, simplifying the addition rule by setting the probability of their intersection to zero.
Independent events are those where the outcome of one does not affect the outcome of the other.
Mutually exclusive events cannot be independent, which is a key concept for probability calculations.
Conditional probability is calculated by considering the outcome of one event affecting the outcome of another.
Two-way tables are useful for calculating probabilities in surveys or studies, demonstrated with an example.
Conditional probability can be visualized and calculated using tree diagrams for complex scenarios.
The probability of a positive test result does not necessarily indicate the presence of a condition, as shown with a dog heartworm test example.
Multiplying probabilities is essential for calculating the likelihood of multiple independent events occurring in sequence.
Building a probability model involves considering all possible outcomes and their respective probabilities.
The probability of independent events can be calculated by simply multiplying their individual probabilities.
Understanding the difference between dependent and independent probabilities is crucial for accurate calculations.
Normal distribution and its use in probability calculations are essential for certain AP Statistics problems.
The importance of recognizing when the normal model is applicable in probability problems.
Binomial probability will be covered in a separate video, indicating the breadth of topics in AP Statistics.
Transcripts
Browse More Related Video

Probability Formulas, Symbols & Notations - Marginal, Joint, & Conditional Probabilities

Chapter 4 Probability Part 2

Elementary Stats Lesson #8

4.2.3 Addition and Multiplication Rules - Disjoint Events and Implications for Probability

Multiplication & Addition Rule - Probability - Mutually Exclusive & Independent Events
4.2.1 Addition and Multiplication Rules - Simple and Compound Events, and Their Probabilities
5.0 / 5 (0 votes)
Thanks for rating: