Chapter 4 Probability Part 2
TLDRThis script explores various types of probability calculations, including the addition rule for mutually exclusive events, the subtraction rule for overlapping events, and the multiplication rule for independent events. It also delves into conditional probability and dependent events, providing examples such as blood type distribution, student surveys, and medical outcomes. The script aims to clarify the concepts by demonstrating how to calculate probabilities in different scenarios, emphasizing the importance of understanding the relationship between events.
Takeaways
- 📚 Compound events are formed by combining two or more simple events using 'and' or 'or', with different calculations for mutually exclusive and overlapping events.
- 🔢 For mutually exclusive events, the probability is found by adding the individual probabilities without overlap.
- 🤔 Overlapping events require the subtraction of the overlapping probability to avoid double counting when calculating the combined probability.
- 📊 An example given was a survey with responses categorized as favoring, opposing, or having no opinion on a policy change, illustrating the calculation of combined probabilities.
- 🩸 A blood bank example showed how to calculate the probability of a donor having type B blood or Rh positive blood, including handling overlaps.
- 👥 The script explains how to handle relative frequencies and total populations in probability calculations when a total is not given.
- 🌹 An example of independent events was given with Joanna selecting flowers from a vase, where the probability of selecting a rose twice is the product of individual probabilities.
- ❤️ The multiplication rule for independent events was illustrated, showing how to calculate the probability of two events both occurring.
- 🔄 Dependent events, where one event affects the probability of another, were explained, using an iPod giveaway as an example of 'without replacement'.
- 🎓 Conditional probability was defined as the probability of an event given that another event has already occurred, with examples from a hospital patient survey.
- 📉 The script provided examples of calculating conditional probabilities, such as the likelihood of satisfaction with surgery outcomes based on the type of surgery performed.
Q & A
What is a compound event in probability theory?
-A compound event in probability theory is an event that is formed by combining two or more simple events using the words 'and' or 'or'. It represents the occurrence of multiple events simultaneously or in sequence.
How is the probability of mutually exclusive events calculated?
-The probability of mutually exclusive events is calculated by summing the individual probabilities of each event. Since these events cannot occur simultaneously, their combined probability is the sum of their individual probabilities.
What is the difference between mutually exclusive and overlapping events?
-Mutually exclusive events are those that cannot happen at the same time, with no overlap in their probabilities. Overlapping events, on the other hand, can occur simultaneously, and there is an overlap in their probabilities which must be accounted for to avoid double-counting.
How do you calculate the probability of a random person surveyed opposing or having no opinion about a policy change?
-To calculate this, you would find the individual probabilities of someone opposing the policy change and someone having no opinion, then add these probabilities together since these are mutually exclusive events.
What is the correct probability calculation for the survey example given in the script?
-The correct calculation should be the sum of the probabilities of opposing (37/100) and having no opinion (36/100), which equals 0.73 or 73%.
How is the probability of a donor having type B blood or Rh positive blood calculated?
-The probability is calculated by adding the individual probabilities of having type B blood and Rh positive blood, then subtracting the probability of the overlap (those who have both type B and Rh positive blood) to avoid double-counting.
What is the concept of independent events in probability?
-Independent events are events where the occurrence of one event does not affect the probability of the occurrence of another event. The probability of both events happening is found by multiplying their individual probabilities.
How is the probability of dependent events calculated?
-For dependent events, where the occurrence of one event affects the probability of the other, the calculation involves multiplying the probability of the first event by the conditional probability of the second event given the first.
What is conditional probability and how is it calculated?
-Conditional probability is the probability of an event occurring given that another event has already occurred. It is calculated by dividing the probability of both events occurring by the probability of the event that is given.
Can you provide an example of calculating conditional probability from the script?
-An example from the script is determining the probability that a person was satisfied with their surgery given that they had knee surgery. This would be calculated as the number of satisfied knee surgery patients over the total number of knee surgery patients.
What is the importance of understanding the difference between 'with replacement' and 'without replacement' in probability problems?
-Understanding 'with replacement' and 'without replacement' is crucial because it affects the total number of outcomes and thus the probability calculation. 'With replacement' means the total number of outcomes remains the same after each event, while 'without replacement' means the total decreases as events occur.
Outlines
📊 Understanding Compound Event Probabilities
This paragraph explains the concept of compound event probabilities, which are calculated by combining the probabilities of two or more simple events. It distinguishes between mutually exclusive events, where the probability is the sum of individual probabilities, and overlapping events, where the overlap must be subtracted to avoid double-counting. An example using a survey about change and policy is provided, illustrating how to calculate the probability of a respondent opposing or having no opinion on the matter. The summary also corrects a mistake in the calculation, emphasizing the importance of accurate arithmetic in probability assessment.
🧬 Probabilities with Overlapping and Independent Events
The second paragraph delves into the calculation of probabilities involving overlapping and independent events. It uses the example of a blood bank cataloging blood types to demonstrate how to account for overlaps when calculating the probability of a donor having type B blood or being Rh positive. The paragraph also discusses the multiplication rule for independent events, as illustrated by the probability of selecting a rose twice from a vase in a series of random selections. The summary corrects the probabilities provided in the script and emphasizes the importance of understanding the relationship between events when calculating probabilities.
🔄 Dependent Events and Conditional Probability
This paragraph introduces the concepts of dependent events and conditional probability. It explains that dependent events occur when the occurrence of one event affects the probability of another, often in scenarios without replacement. The paragraph provides an example of an iPod giveaway to illustrate the calculation of dependent probabilities. It also explains conditional probability, which is the probability of an event given that another event has already occurred, using a survey of surgery patients as an example. The summary highlights the importance of considering the total outcomes based on given information when calculating conditional probabilities.
📉 Calculating Conditional Probabilities in Surveys
The final paragraph focuses on calculating conditional probabilities using data from a survey of surgery patients. It demonstrates how to determine the probability of satisfaction or dissatisfaction with surgery results based on specific types of surgery. The paragraph emphasizes the importance of using the correct totals and given information to calculate accurate probabilities. The summary provides corrected probabilities and illustrates the step-by-step process of calculating conditional probabilities in the context of survey results.
Mindmap
Keywords
💡Compound Event
💡Mutually Exclusive Events
💡Overlapping Events
💡Relative Frequency
💡Independent Events
💡Dependent Events
💡Conditional Probability
💡Without Replacement
💡Probability Calculation
💡Survey Data
Highlights
Introduction to compound events and their calculation using 'and' or 'or'.
Explanation of how to calculate probabilities for mutually exclusive events by summing individual probabilities.
Clarification on handling overlapping events in probability calculation by subtracting the overlap to avoid double counting.
Example of calculating the probability of a respondent opposing or having no opinion on policy change from a survey.
Illustration of probability calculation for blood type B or Rh positive using a blood bank's data, including handling overlaps.
Misinterpretation correction: The correct probability calculation for opposed or no opinion should result in 0.55, not 0.73.
Demonstration of how to find the total and calculate relative frequency when a total is not provided.
Use of a survey to determine the probability of students being seniors or reading a daily paper, accounting for overlap.
Introduction to the multiplication rule for calculating the probability of independent events occurring together.
Example of calculating the probability of selecting a rose twice in a row from a vase of flowers.
Misinterpretation correction: The correct probability for selecting a rose twice should be approximately 0.16.
Explanation of calculating the probability of dependent events, where the outcome of one event affects the other.
Example of calculating the probability of choosing an orange iPod by two people without replacement.
Introduction to conditional probability and its calculation based on given events.
Example of determining the probability of satisfaction with surgery results given that the surgery was on the knee.
Misinterpretation correction: The correct probability for dissatisfied patients with hip surgery should be approximately 0.143.
Example of calculating the probability of a patient having heart surgery given dissatisfaction with the surgery results.
Transcripts
cow pal probabilities a compound event
combines two or more simple events using
the word an or the word or when we're
working with mutually exclusive events
the probability is found by summing the
individual probabilities of the events
so if we have a probability of A or B
what you would do to find the
probability is find the probability of a
and then find the probability of B and
add them together when we have
overlapping events the events are not
mutually exclusive so mutually exclusive
has no overlap in the probability but
when we have overlapping events the
probability that overlapping events a
and B or both will occur is expressed as
so the probability of a or the
probability of B would equal you would
find the probability of a you would add
it to the probability of B but then you
would need to subtract out the
probability of that overlap so whatever
the overlap is so you're not including
that value twice so you always have to
subtract out the overlap so let's do an
example here in a survey about change
and policy a hundred people were asked
if they favor it opposed or had no
opinion so you see the values in the
table that we have here now we're asked
to find the probability that a randomly
selected responded to the survey opposed
or had no opinion about the change of
policy so we're looking at the opposed
or no opinion so we're finding that that
that the probability is mutually
exclusive because there's no overlap in
these events so when I find the
probability I'm going to find the
probability of a pose
and a probability of no opinion and I'm
going to add them together so a
probability of opposed would be that 37
over a hundred plus the probability of
no opinion would be 36 over a hundred so
when I add this together I end up
getting 73 over a hundred or it would
equal point seven three or 73% pause and
try so in this case you should have
ended up with 0.55 as the probability
pause and try and in this case you would
end up with 0.35 as your probability
pause and try now remember when you have
a relative frequency if you don't have a
total you're going to have to find the
total and in this case the total was 36
and when you find the probability you
end up with point four four four so
let's do an example here a blood bank
catalogs the type of blood given by
donors during the last five days a donor
is selected at random we want to find
the probability the donor has type B or
is Rh positive so what we're looking at
this table when we look at type B the
type B is a total of forty five out of
the 409 and the positive or the H of the
Rh positive we have a total of three
hundred and forty four out of the 409
that have positive blood type so when we
look at this you can see that we have an
overlap of thirty seven meaning that the
type B the 37 was added in the total for
forty five and for the positive that 37
was added into the total of three forty
four so because it's added in both
totals you cannot include it in both of
your profit
oh these so when you're doing the
probability you're going to need to take
out the overlap the the doubling of that
37 so how to do this you want to find
the probability of B first which would
be that 45 over 409 and then you're
going to find the probability of
positive which would be that 344 over
409 and then you want to subtract out
one of those 37 because you used it
twice so you only need to subtract out
one so you're going to subtract out the
37 over 409 to find the actual
probability of this so this is that
overlap that needs to be subtracted out
so your probability for being a type B
or Rh positive would be point eight six
one pause and try so in this case you
should have gotten a probability of 0.8
four zero pause and try so in this case
you should have gotten a probability of
0.85 one pause and try so this
probability is point six nine three
pause and try and this probability is
point nine nine five this next example
is we don't have a table so we can't see
the overlap we need to define what the
overlap is so of fifteen hundred and
sixty students surveyed 840 were seniors
and six thirty read a daily paper the
rest of the students were juniors only
two hundred fifteen of the papers read
were juniors now we're asked to find the
probability that a student was a senior
or read the daily paper read a daily
paper so when you're looking at this we
want the probability of a senior so we
can find that easily
now when we find the order and the
Orbeez we're adding the readers the
probability of readers we have this six
thirty over the fifteen sixty but you
have to be careful here because we have
an overlap and the overlap is the
seniors that read the paper the daily
paper so how to find the senior total
that read the daily paper is you have to
go by the information that's given and
the information here that's given is
we're told that out of those six hundred
and thirty readers two hundred fifteen
of them are the juniors so to find the
seniors we need to take the six thirty
and subtract out the juniors so the
total for the readers for that were
seniors were that four hundred and
fifteen so that's my overlap here that
415 seniors that read and I need to take
that overlap out and then for in order
to find this true probability so we end
up with 0.67 6 as our probability pause
and try so this is similar here where we
have a probability where a hundred sixty
beauty spas customers were surveyed and
ninety six had hairstyle and 61 had
manicures and you see here they're
telling you the twenty eight of the
customers only had manicures so that is
an overlap when we talk about the
combination of hairstyle and manicures
so you need to take the 61 and subtract
the twenty eight to find the overlap of
people who had the hair style and
manicure which is that 33 so you should
have gotten a probability of point seven
seven five
pause and try so again that overlap is
that 52 and you should have gotten a
probability of 0.6 1 so the next type of
compound probability when we have
independent events and two events a and
B are independent if a occurs and it
doesn't affect the probability of B
we're going to be using the
multiplication rule for the probability
of a and B happening so when we're
talking about the probability of a and B
we're going to be multiplying and you
see you're going to multiply the
probability of A to the multiply to the
probability of B so we have an example
here where Joanna has three roses for
tulips and one carnation in a vase she's
gonna randomly select one flower she
took up photo and took a photo of it and
put it back
she then repeats these steps what is the
probability she selected a rose both
times so you want to find the
probability of her selecting a rose both
times and because she put the first
flower back that doesn't change the
total when she selects the second rose
so when you're doing the probability
here you're going to find the
probability of it being a rose the first
time and then you're going to find the
probability of it being a rose the
second time so when you do the
probability here you're going to
multiply the probability of a rose which
is three out of eight times the
probability of a the second one being a
rose which would be three out of eight
and when you get this probability you're
going to end up with approximately point
four point one at four one pause and try
so in this case you should have gotten a
probability of 0.16
pause and try so this one you're given
the probabilities already it's a 90
percent chance of survival so we have
that and the patient is 45 percent
chance of heart damage you're given that
so when you're finding the probability
of survival and heart damage heals
you're going to multiply the two
probabilities together you say you
should have ended up with point four
zero five pause and try so in this case
you're going to multiply the point eight
five to itself three times and you get
point six one
so now this next one is when we have
dependent events two events a and B are
dependent if a occurs and it affects the
probability of B occurring so dependent
will affect the second probability so a
probability of a and B occurring we
would end up having the probability of a
times the probability of a given that a
already happened so a lot of times you
might not have you might have in there
the words without replacement so if
you're taking something out then the
total is going to change if it says it's
without replacement so a key note here
sometimes a problem will not
specifically state whether it is a
problem with or without replacement but
you have to use your own common sense
when it comes to a probability problem
if we're talking about people maybe
going on a trip and you're going to
choose five of your friends we can't and
you're going to choose two out of the
five we can't choose the same friend
twice so it will be a dependent event so
let's do this example here Best Buy is
having an iPod giveaway they put all
the iPod shuffles in a bag customers may
choose an iPod without looking at the
color inside the bag there are four
orange five blue six green and five pink
iPods if Maria chooses one iPod at
random and that her sister chooses one
PI iPod at random what's the probability
they are both choosing an orange iPod so
again the first thing you're going to
need here is you're going to need some
type of total so you're going to have to
actually add four plus five plus six
plus five together you need your totals
now when we get that total we want to
find the probability of orange Maria
getting an orange and then the
probability of her sister getting an
orange now in this case it's not telling
me whether it's replaced or not though
if she if Maria is choosing an iPod
she's going to keep it she's not going
to put it back in so when you're finding
the probability you're going to end up
with Maria's probability is going to be
four out of 20 but because Maria's not
given our iPod back her sister is going
to choose an iPod and it's going to
change the value of the probability if
Maria has a orange iPod then there's
only three oranges left and the total
number of iPods change because Maria
kept her iPod so you end up having three
over nineteen as her sister's
probability and when you multiply this
together you should get a probability of
approximately point zero three two so
again when you have a probability less
than point zero five it's unlikely
something like this would happen
pause and try so in this case you should
have gotten point four six seven pause
and try
so in this case you should have gotten
point two eight six pause and try so in
this case you should have gotten approx
point two nine four the next type of
probability we're going to work with is
a conditional probability and a
conditional probability is the
probability of an event occurring given
that another another event has already
occurred okay so the probability of B
given a so you see how it would be
written in the probability denoted a key
note here is that the total outcome is
always going to be based on the given so
when we're looking at probabilities
remember the probability is based on
totals so you need a total but in a
conditional probability the total is
going to be based on the given because
we're already told something and that
eliminates everything else that is not
part of that given information so let's
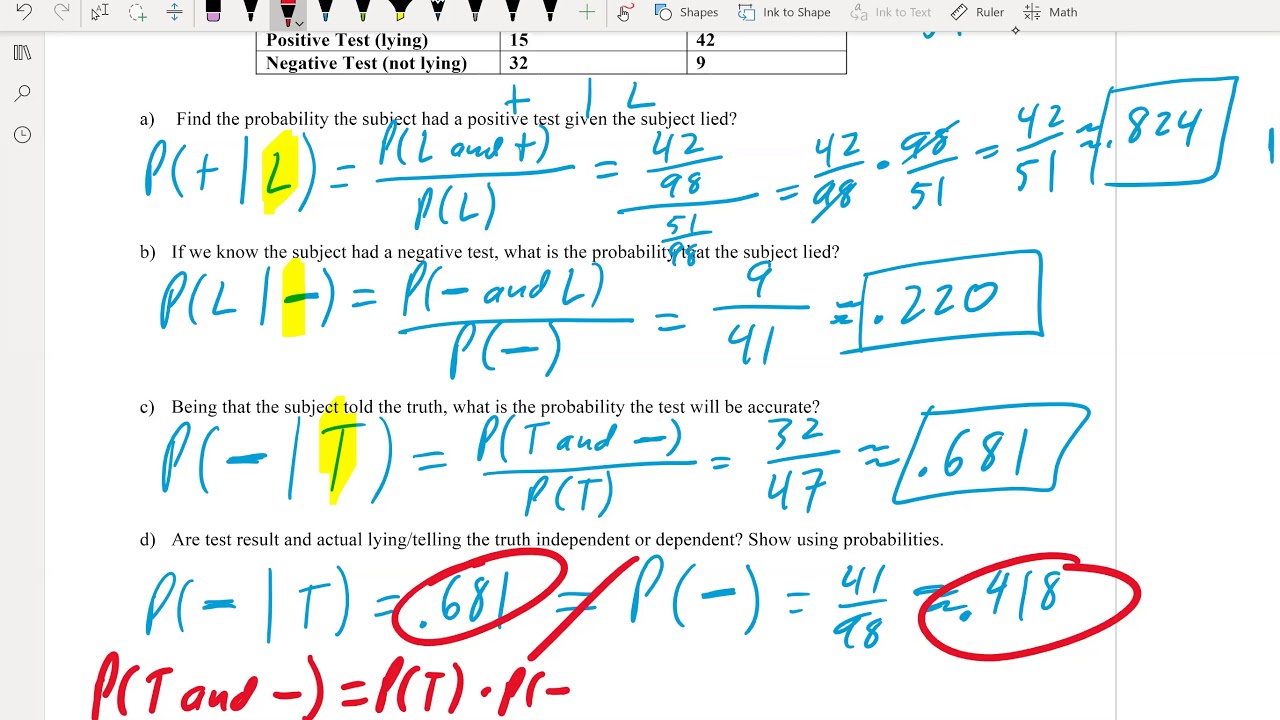
do an example here survey given to
surgery patients at a given Hospital
results are displayed in the table below
determine the probability that the
person was satisfied with the results of
their surgery given that the person had
knee surgery so we already know that the
person had knee surgery so because we
know that our total is going to be based
on the fact that they've knee surgery so
the total in this probability is going
to be 95 that is the net total number of
knee surgery everything else doesn't
matter because we already know that it's
based on the fact they had knee surgery
and that they were satisfied is going to
be the seventy in the satisfied for knee
surgery so this probability here would
be 70 over 95 or approximately point
seven
3:7 so we're using the same example but
we're asked determine the probability
was dissatisfied with the results of the
survey surgery given that the person had
hip surgery so now the given is based on
the hip surgery and the hip surgery
total is that fought 105 so because the
given is the hip surgery we know that
it's in hip surgery the dissatisfied is
that 15 so then we end up with 15 over
105 which is approximately 0.14 3 and
this next example you see the same
determine the probability that the
person had heart surgery given that the
person was dissatisfied with the results
of the survey or surgery so again
dissatisfied is the total of 45 so we
need to use the total of dissatisfied
surgeries and then we look at what we're
looking for the probability so it would
be 5 divided by 45 which is
approximately 0.1 1 pause and try so in
this case you should have gotten point 3
6 0 pause and try so in this case you
should have gotten 0.375 pause and try
so here we should have gotten point 3 1
6 pause and try this you should have
gotten point 6 2 5 pause and try this
you should have gotten point 2 2 2 pause
and try
this you should have gotten point 796
pause and try this you should have
gotten point one seven eight pause and
try this you should have gotten point
one five four pause and try and this you
should have gotten point four two nine
Browse More Related Video

4.2.3 Addition and Multiplication Rules - Disjoint Events and Implications for Probability

AP Stats Test Quick Review: Probability

Probability Formulas, Symbols & Notations - Marginal, Joint, & Conditional Probabilities

Elementary Stats Lesson #8
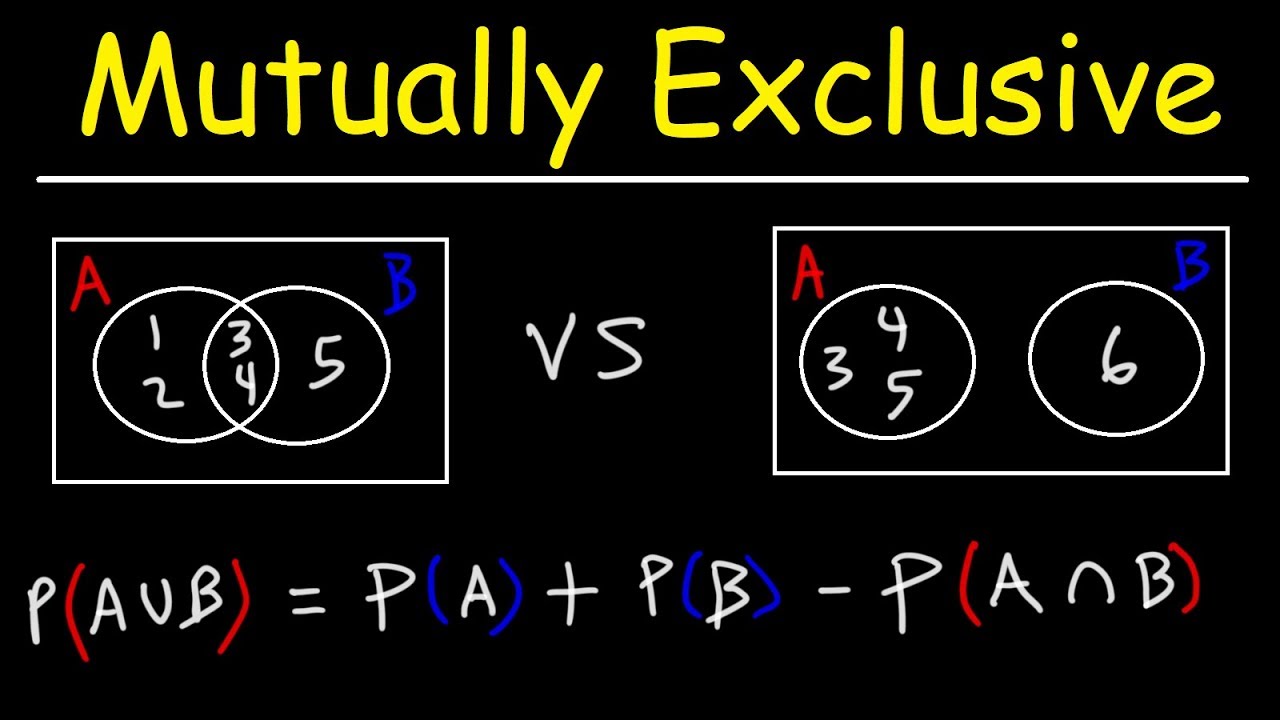
Probability of Mutually Exclusive Events With Venn Diagrams
Math 119 Chapter 4 part 3
5.0 / 5 (0 votes)
Thanks for rating: