Consumer/Producer Surplus

PClark Calc
17 Apr 202009:33
EducationalLearning
32 Likes 10 Comments

TLDRIn this video, Pete Clark explores the business application of consumer and producer surplus in calculus, demonstrating how these concepts measure the overall benefit to consumers and producers in a free market economy. The video uses a quadratic demand function and a linear supply function to illustrate market equilibrium, and then calculates the surpluses by integrating the area between the curves and the equilibrium price. The process is explained with clarity, making it accessible for students looking to understand the practical applications of calculus in economics.

Takeaways
  • 📚 The video discusses a business application of calculus known as consumer and producer surplus, which measures the overall benefit to consumers or producers in a free market economy.
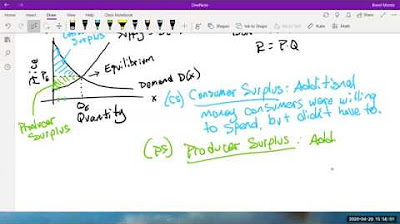
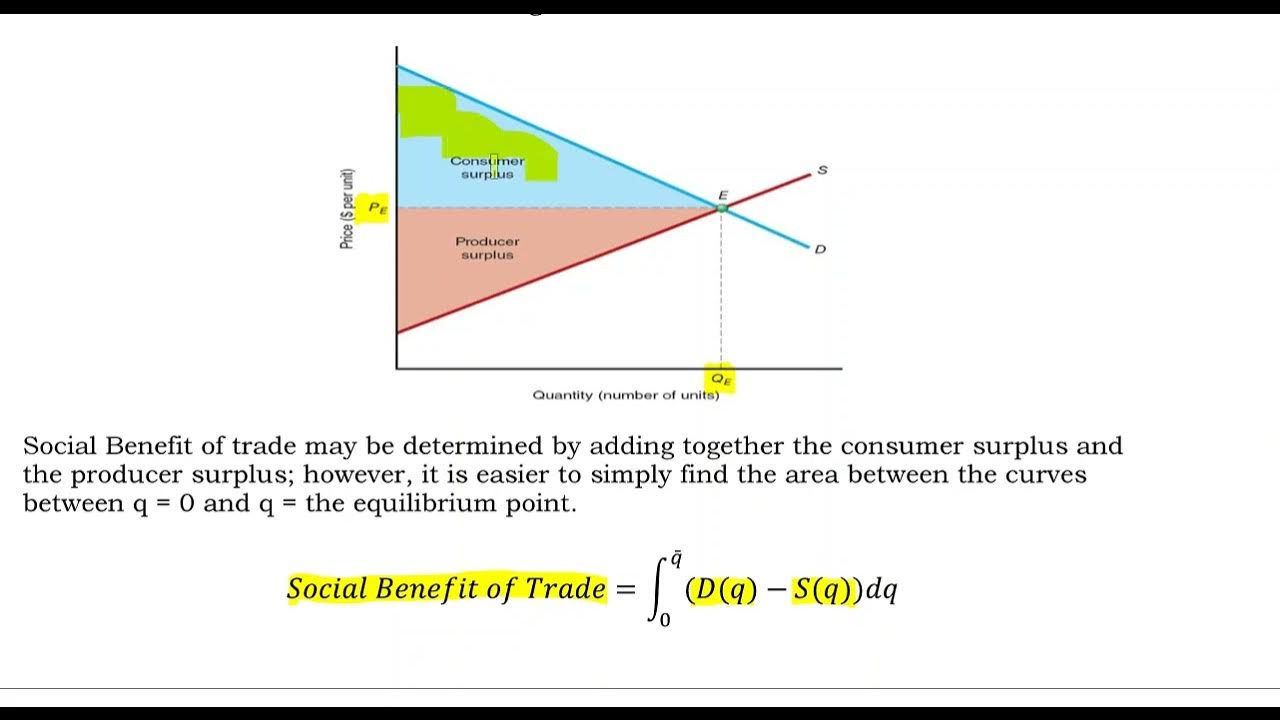
  • 📈 Consumer surplus is the area between the demand curve and the market equilibrium price, representing the total amount consumers benefit by paying less than they are willing to pay.
  • 📉 Producer surplus is the area between the supply curve and the market equilibrium price, indicating the total amount producers benefit by earning more than they are willing to accept.
  • 🔍 The market equilibrium is the intersection point of the supply and demand curves, determining the market price of goods in a free market economy.
  • 📝 The example provided uses a demand function D(x) = 200 - 0.5x^2 and a supply function S(x) = 10x + 50, which intersect at the market equilibrium point (10, 150).
  • 🧮 To calculate consumer surplus, integrate the demand function minus the market price from 0 to the equilibrium quantity, resulting in a consumer surplus of approximately $333.33.
  • 📐 To calculate producer surplus, integrate the market price minus the supply function from 0 to the equilibrium quantity, which in this case forms a right triangle with a surplus of $500.
  • 🤔 The concept of surpluses helps to understand the benefits consumers and producers receive from market transactions at the equilibrium price.
  • 📚 The video script is from a series that applies calculus to business scenarios, specifically focusing on the area between curves in the context of consumer and producer surplus.
  • 📘 The speaker, Pete Clark, offers textbooks for further study on these topics, available on Amazon, and encourages viewers to subscribe to his channel for more educational content.
  • 📝 The integrals for calculating surpluses are defined by the difference between the respective curves (demand or supply) and the market equilibrium price over the range of the equilibrium quantity.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the business application of the area between curves, specifically focusing on consumer and producer surplus in the context of economics and calculus.

  • What is consumer surplus?

    -Consumer surplus is the difference between the price consumers are willing to pay and the market price they actually pay for a good or service. It represents the overall benefit to consumers due to the free market price being lower than what they would have paid.

  • What is producer surplus?

    -Producer surplus is the difference between the market price and the price producers are willing to accept for a good or service. It represents the overall benefit to producers because they are earning more than their minimum willingness to accept.

  • How is market equilibrium defined in the context of the video?

    -Market equilibrium is defined as the point where the supply and demand curves intersect. It determines the market price and quantity of goods that will be exchanged in a free market economy.

  • What are the functions used to model demand and supply in the video example?

    -The demand function is modeled as a quadratic function, D(x) = 200 - 0.5x^2, and the supply function is an increasing linear function, S(x) = 10x + 50.

  • What is the market equilibrium price and quantity found in the video example?

    -The market equilibrium price is $150, and the equilibrium quantity is 10 units, found by solving the intersection of the demand and supply functions.

  • How is consumer surplus calculated in the video?

    -Consumer surplus is calculated by integrating the difference between the demand function and the market price from 0 to the equilibrium quantity (x=10).

  • What is the result of the consumer surplus calculation in the video?

    -The consumer surplus is found to be $333.33, calculated by evaluating the integral of the demand function minus the market price over the specified bounds.

  • How is producer surplus calculated in the video?

    -Producer surplus is calculated by integrating the difference between the market price and the supply function from 0 to the equilibrium quantity (x=10).

  • What is the result of the producer surplus calculation in the video?

    -The producer surplus is found to be $500, which can be calculated either by integrating the given function or by recognizing the area as a right triangle and using the formula for the area of a triangle (1/2 * base * height).

Outlines
00:00
📚 Introduction to Consumer and Producer Surplus

This paragraph introduces the concept of consumer and producer surplus in the context of business calculus. It explains how these surpluses measure the overall benefit to consumers and producers due to the free market price of a product. The consumer surplus is the area between the demand curve and the market equilibrium price, representing the amount consumers are willing to pay above the market price. Conversely, the producer surplus is the area between the supply curve and the market equilibrium price, indicating the amount producers are willing to accept below the market price. The paragraph sets the stage for a detailed explanation of how these surpluses are calculated using the intersection of supply and demand curves, specifically with a given quadratic demand function and a linear supply function.

05:02
📈 Calculating Consumer and Producer Surplus

The second paragraph delves into the actual calculation of consumer and producer surplus using the derived market equilibrium from the previous paragraph. It first calculates the consumer surplus by integrating the difference between the demand function and the market price from 0 to the equilibrium quantity. The integral is simplified and evaluated, resulting in a consumer surplus of $333.33. The paragraph then explains the producer surplus, which is calculated similarly but as the area between the market price and the supply function. A shortcut using the geometric interpretation of the integral as a right triangle is employed to find the producer surplus, which is $500.

Mindmap
Keywords
💡Consumer Surplus
Consumer surplus is the difference between the price a consumer is willing to pay for a good or service and the market price they actually pay. It represents the perceived benefit or 'extra value' that consumers gain from participating in a market. In the video, consumer surplus is calculated by integrating the demand function minus the market price over the range of quantity demanded, which in this case is from 0 to 10 units. The script provides an example of a consumer willing to pay more than the market price, but only having to pay the market price, thus gaining a surplus.
💡Producer Surplus
Producer surplus is the difference between the market price received by producers for a good or service and the price they are willing to accept. It reflects the additional profit or 'extra gain' that producers make from selling at the market price. In the video, the script explains that producer surplus is the area between the market price and the supply function, calculated as the integral of the market price minus the supply function from 0 to the equilibrium quantity, which is 10 units in the example.
💡Market Equilibrium
Market equilibrium is the point at which the supply and demand for a product intersect, resulting in a stable market price and quantity. It is a fundamental concept in economics where the quantity demanded by consumers equals the quantity supplied by producers. The video script describes the market equilibrium as the intersection of the demand and supply functions, which determines the price of items in a free market economy.
💡Demand Function
A demand function is a mathematical representation of the quantity of a product that consumers are willing to purchase at various price levels. It typically shows a negative relationship between price and quantity demanded. In the video, the demand function is given as a quadratic equation, D(x) = 200 - 0.5x^2, which decreases as the quantity demanded increases, reflecting the law of demand.
💡Supply Function
A supply function represents the quantity of a product that producers are willing to supply at various price levels. It usually shows a positive relationship between price and quantity supplied. In the video, the supply function is an increasing linear function, S(x) = 10x + 50, indicating that as the price increases, the quantity supplied also increases.
💡Quadratic Equation
A quadratic equation is a polynomial equation of degree two, which can be used to model various phenomena, including demand functions in economics. The video script mentions solving a quadratic equation to find the market equilibrium, where the demand and supply functions intersect, resulting in the equilibrium quantity of 10 units.
💡Integral
In calculus, an integral is a mathematical concept that represents the area under a curve between two points. In the context of the video, integrals are used to calculate consumer and producer surplus by integrating the demand function minus the market price and the market price minus the supply function, respectively, over the range of the equilibrium quantity.
💡Antiderivative
An antiderivative is a function that represents the reverse process of differentiation. It is used to find the area under a curve by integrating. The video script explains that the antiderivative of the function representing consumer surplus is used to evaluate the definite integral and find the consumer surplus amount.
💡Power Rules
Power rules are a set of mathematical rules used to integrate polynomial functions. They state that the integral of x^n, where n is a constant, is x^(n+1)/(n+1) + C, where C is the constant of integration. The video script refers to power rules when integrating the demand function to find the consumer surplus.
💡Geometric Interpretation
Geometric interpretation involves understanding mathematical concepts through their visual or spatial representation. In the video, the producer surplus is calculated using a geometric interpretation, where the area under the curve is represented as a right triangle, and the area is found using the formula for the area of a triangle, 1/2 * base * height.
💡Economic Benefit
Economic benefit refers to the advantage or gain that individuals or entities derive from economic activities. In the video, both consumer and producer surplus are described as forms of economic benefit, where consumers benefit from paying less than they are willing to, and producers benefit from earning more than their minimum acceptable price.
Highlights

Introduction to a specific business application of area between curves known as consumer and producer surplus.

Consumer and producer surplus measures the overall benefit to consumers and producers due to the free market price.

Market equilibrium is the intersection point of supply and demand curves, determining the price of items in a free market economy.

Demand function is modeled as a quadratic equation D(x) = 200 - 0.5x^2.

Supply function is an increasing function, S(x) = 10x + 50, reflecting the increase in supply as price increases.

Market equilibrium is found by setting the demand and supply functions equal to each other and solving for x.

The positive solution to the market equilibrium is x = 10, with an equilibrium price of $150.

Consumer surplus is the area between the demand function and the equilibrium price.

Producer surplus is the area between the market price and the supply function.

Consumer surplus is calculated by integrating the demand function minus the market price from 0 to x0.

Producer surplus is calculated by integrating the market price minus the supply function from 0 to x0.

Calculation of consumer surplus results in a value of $333.33.

Producer surplus can be evaluated geometrically as a right triangle, resulting in a value of $500.

The concept of consumer surplus represents the benefit to consumers for paying less than they are willing to pay.

Producer surplus represents the benefit to producers for earning more than they are willing to accept.

The video provides a practical application of calculus in business, specifically in the calculation of consumer and producer surplus.

The video concludes with an invitation to subscribe to the channel for more content on calculus and its business applications.

Transcripts

Browse More Related Video

Consumer Surplus and Producer Surplus

Consumers' Surplus Producers' Surplus from given Demand and Supply functions

Math 11 - Section 5.1

What is Consumers Surplus and Producer Surplus?

Solving for Consumer, Producer, and Social Surplus using Integration

Social Benefit of Trade (Gains from Trade)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
EconomicsCalculusConsumer SurplusProducer SurplusMarket EquilibriumSupply and DemandBusiness MathIntegral CalculusEconomic BenefitsPete Clark