Uniform Circular Motion Class 11
TLDRThis educational video uses a vinyl record player to illustrate the principles of uniform circular motion. The presenter explains key concepts such as angular displacement, velocity, time period, frequency, and the relationship between linear and angular motion. The video clarifies that uniform circular motion is a type of accelerated motion due to the continuous change in velocity direction, and introduces centripetal acceleration. It also differentiates between uniform and non-uniform circular motion, discussing the role of angular acceleration. The script is interactive, encouraging viewers to calculate linear velocity and centripetal acceleration for a given scenario and engage with the content.
Takeaways
- 😀 The video uses a record player to demonstrate the concept of uniform circular motion, where an object moves in a circle at a constant speed.
- 🎓 Examples of uniform circular motion include the tip of a clock's second hand, rotating fan blades, a Ferris wheel, and a satellite orbiting the Earth.
- 📚 Basic concepts discussed are angular displacement, angular velocity, time period, and frequency, which are essential to understand and describe uniform circular motion.
- 📏 Angular displacement is the angle swept by the radius vector in a certain time interval and can be measured in degrees or radians.
- 👉 Angular displacement's direction is along the axis passing through the center of the circle, determined using the right-hand thumb rule.
- ⚡ Angular velocity is the rate of change of angular displacement with respect to time and is measured in radians per second.
- 🕰 Time period is the time taken for one complete revolution along the circular path, while frequency is the number of revolutions per unit time.
- 🔗 The relationship between linear (tangential) velocity and angular velocity is given by the formula \( V = r \Omega \), where \( V \) is the linear velocity, \( r \) is the radius, and \( \Omega \) is the angular velocity.
- 🚀 In uniform circular motion, even though the speed is constant, the direction of velocity changes continuously, making it an accelerated motion with centripetal acceleration directed towards the center of the circle.
- 🔢 Centripetal acceleration can be calculated using the formulas \( A_C = \frac{V^2}{R} \) or \( A_C = \Omega^2 R \), where \( V \) is the linear velocity and \( \Omega \) is the angular velocity.
- 🌐 The video concludes with a problem-solving exercise asking viewers to calculate linear velocity and centripetal acceleration for a body revolving in a circle, encouraging active engagement with the concepts.
Q & A
What is uniform circular motion?
-Uniform circular motion is when an object moves in a circular path at a constant speed. The speed may be constant, but the direction of the velocity changes continuously, which means there is a centripetal acceleration towards the center of the circle.
What are some examples of uniform circular motion mentioned in the script?
-Examples of uniform circular motion include the tip of the second hand of a clock, rotating fan blades, a Ferris wheel in motion, and a satellite orbiting the Earth.
What is angular displacement and how is it measured?
-Angular displacement is the angle swept by the radius vector as the body moves in a circle. It is measured in degrees or radians, with the SI unit being radians. For instance, a full circle has an angular displacement of 360° or 2π radians.
Can you explain the direction of angular displacement using the right-hand thumb rule?
-Yes, the direction of angular displacement is determined using the right-hand thumb rule. Curl your fingers of the right hand in the direction of the motion, and your thumb will point in the direction of the angular displacement, which is along the axis passing through the center of the circle, either inwards or outwards.
How is angular displacement related to linear displacement?
-Angular displacement is related to linear displacement through the formula s = r * Theta, where s is the linear displacement along the tangent to the circle, r is the radius of the circle, and Theta is the angular displacement in radians.
What is angular velocity and what is its unit?
-Angular velocity is the rate of change of angular displacement with time. It is denoted by the Greek symbol Omega (ω) and its unit is radians per second (rad/s).
How do you calculate the angular velocity of an object that completes a full circle in 2 seconds?
-If an object completes a full circle, which is 2π radians, in 2 seconds, the angular velocity (ω) can be calculated using the formula ω = ΔΘ / ΔT, where ΔΘ is the angular displacement and ΔT is the time. So, ω = 2π rad / 2 s = π rad/s.
What is the relationship between time period (T) and frequency (f) of an object in circular motion?
-The time period (T) is the time taken for one complete revolution, and frequency (f) is the number of revolutions per second. They are reciprocals of each other, with the relationship given by T = 1/f or f = 1/T.
How is linear velocity related to angular velocity?
-Linear velocity (V) is related to angular velocity (ω) by the formula V = r * ω, where r is the radius of the circle. This means that the linear velocity is the product of the radius and the angular velocity.
Why is uniform circular motion considered an accelerated motion?
-Even though the speed (magnitude of velocity) is constant in uniform circular motion, the direction of the velocity is constantly changing. Since acceleration is the rate of change of velocity, and the direction of velocity is changing, the object is experiencing centripetal acceleration towards the center of the circle.
What are the formulas for centripetal acceleration in terms of linear velocity and angular velocity?
-Centripetal acceleration can be expressed in terms of linear velocity as AC = V² / R, where V is the linear velocity and R is the radius of the circle. Alternatively, in terms of angular velocity, it can be expressed as AC = ω² * R, where ω is the angular velocity.
How can you find the net acceleration in circular motion with both angular and linear accelerations?
-The net acceleration in circular motion, where there are both centripetal and tangential accelerations, can be found using the Pythagorean theorem: a_net = √(a² + AC²), where a is the tangential acceleration and AC is the centripetal acceleration.
What is the challenge presented at the end of the script regarding a body revolving in a circle?
-The challenge is to calculate the linear velocity and centripetal acceleration experienced by a 5 kg body revolving in a circle of diameter 14 cm at 300 RPM (revolutions per minute).
Outlines
📀 Introduction to Uniform Circular Motion
The script begins with an introduction to the concept of uniform circular motion using a record player as a practical example. The speaker thanks the YouTube team for the gift and places a coin on the record player to demonstrate circular motion. The coin's constant speed as it moves in a circle illustrates the definition of uniform circular motion. Examples such as the tip of a clock's second hand, rotating fan blades, a merry-go-round, and a satellite orbiting Earth are given to contextualize the concept. The speaker then introduces the basic concepts needed to understand and describe uniform circular motion, such as angular displacement, angular velocity, time period, and frequency, and promises to delve into these concepts in detail.
📐 Angular Displacement and Linear Displacement
This paragraph delves into the concepts of angular displacement and linear displacement. Angular displacement is defined as the angle swept by the radius vector as the body moves in a circle, with examples given for 60°, 90°, and 180° angles, culminating in a full circle at 360° or 2π radians. The right-hand thumb rule is introduced to determine the direction of angular displacement, which is along the axis of the circle. The relationship between linear displacement (along the circle's tangent) and angular displacement is then discussed, with the formula Θ = s/R derived, where Θ is the angle, s is the arc length, and R is the radius. The paragraph concludes with a practical demonstration using two coins placed at different radii from the center of the circle, showing that while both coins have the same angular displacement, their linear displacements differ due to the different radii.
⏱ Time Period, Frequency, and Angular Velocity
The script continues by explaining the concepts of time period and frequency in the context of circular motion. The time period is the duration for one complete revolution, while frequency is the number of revolutions per unit time. The relationship between time period (T) and frequency (f) is given by the reciprocal relationship T = 1/f and f = 1/T. Angular velocity (Ω), the rate of change of angular displacement over time, is then discussed, with the formula Ω = ΔΘ/ΔT provided, where ΔΘ is the change in angle and ΔT is the change in time. The units of angular velocity are radians per second. An example calculation is given for a coin rotating through 2π radians in 2 seconds, resulting in an angular velocity of π radians per second. The paragraph also differentiates between average and instantaneous angular velocity, with the latter obtained through calculus as the limit of ΔT approaches zero.
🚀 Relationship Between Linear Velocity and Angular Velocity
This section establishes the relationship between linear velocity (also known as tangential velocity) and angular velocity. Linear velocity is defined as the rate of change of linear displacement, with the formula V = ΔS/ΔT, where ΔS is the change in displacement and ΔT is the change in time. By using the relationship angle = Arc/Radius, the formula for angular velocity Ω = ΔΘ/ΔT is connected to linear velocity, resulting in the formula V = RΩ, where R is the radius of the circle. The paragraph demonstrates with an example of two bodies at different radii that, despite having the same angular velocity, will have different linear velocities due to their different distances from the center. The importance of the formula V = RΩ in understanding the connection between linear and angular velocities is emphasized.
🔁 Acceleration in Uniform Circular Motion
The script addresses the misconception that uniform circular motion is not an accelerated motion due to the constant speed. It explains that even though the speed (magnitude of velocity) is constant, the direction of the velocity is continuously changing, which means the velocity vector is changing, and thus the body is accelerating. This type of acceleration is called centripetal acceleration, as it is directed towards the center of the circle. The formula for centripetal acceleration (AC) is introduced, with two forms: AC = V²/R and AC = Ω²R, where V is the linear velocity and Ω is the angular velocity. The paragraph clarifies that in uniform circular motion, the only acceleration present is centripetal acceleration, as there is no change in the magnitude of velocity, only its direction.
🌀 Angular and Linear Acceleration in Non-Uniform Circular Motion
The final paragraph extends the discussion to non-uniform circular motion, where the speed of the object changes, resulting in angular and linear acceleration. Angular acceleration (α) is defined as the rate of change of angular velocity, with the formula α = ΔΩ/ΔT. The unit of angular acceleration is radians per second squared. The relationship between angular acceleration and linear (or tangential) acceleration is explored through the equation a = Rα, where a is the linear acceleration and R is the radius of the circle. The paragraph explains that in non-uniform circular motion, an object experiences both centripetal acceleration (towards the center of the circle) and tangential acceleration (along the tangent to the circle), which are perpendicular to each other. The net acceleration is calculated using the Pythagorean theorem, as the two accelerations are vector quantities at right angles to each other.
📚 Application and Learning Opportunities with Manoa Academy
The script concludes with a practical problem for the audience to solve, involving calculating linear velocity and centripetal acceleration for a body revolving in a circle. The speaker invites viewers to share their answers in the comments and promises to reply. The video also promotes the Manoa Academy's offerings, including live classes, interactive videos, quizzes, mock tests, and revision notes across various subjects like physics, chemistry, biology, maths, coding, and artificial intelligence. The speaker encourages viewers to subscribe to their YouTube channel, turn on notifications, and visit their website or try their Android app for a free trial of the courses.
Mindmap
Keywords
💡Uniform Circular Motion
💡Angular Displacement
💡Radius Vector
💡Angular Velocity
💡Time Period
💡Frequency
💡Linear Displacement
💡Centripetal Acceleration
💡Angular Acceleration
💡Linear Acceleration
Highlights
Introduction to the concept of uniform circular motion using a record player and a coin.
Explanation of uniform circular motion as constant speed in a circular path.
Examples of uniform circular motion: clock second hand, fan blades, merry-go-round, and satellite orbiting Earth.
Basic concepts of angular displacement, velocity, time period, and frequency in circular motion.
Demonstration of angular displacement with the coin on the record player.
Conversion between degrees and radians for angular displacement.
Direction of angular displacement using the right-hand thumb rule.
Relation between angular displacement and linear displacement with the formula s = r * Theta.
Illustration of linear displacement difference with coins at different radii.
Definition and formula of angular velocity, including its unit in radians per second.
Calculation of angular velocity for the coin using the formula.
Definition of time period and frequency, and their reciprocal relationship.
Derivation of the relation between angular velocity, time period, and frequency.
Introduction to linear velocity and its relation to angular velocity with the formula v = r * Omega.
Differentiation between uniform circular motion (constant speed) and variable speed circular motion.
Explanation of centripetal acceleration in uniform circular motion and its formula.
Differentiation between centripetal, angular, and linear acceleration in circular motion.
Calculation of centripetal acceleration using both tangential velocity and angular velocity.
Challenge problem presented to calculate linear velocity and centripetal acceleration for a given scenario.
Invitation to subscribe to the YouTube channel and try free courses on manoch academy.com.
Transcripts
Browse More Related Video

AP Physics C: Rotational Kinematics Review (Mechanics)
Circular Motion: Acceleration (Angular, Tangential, Centripetal)
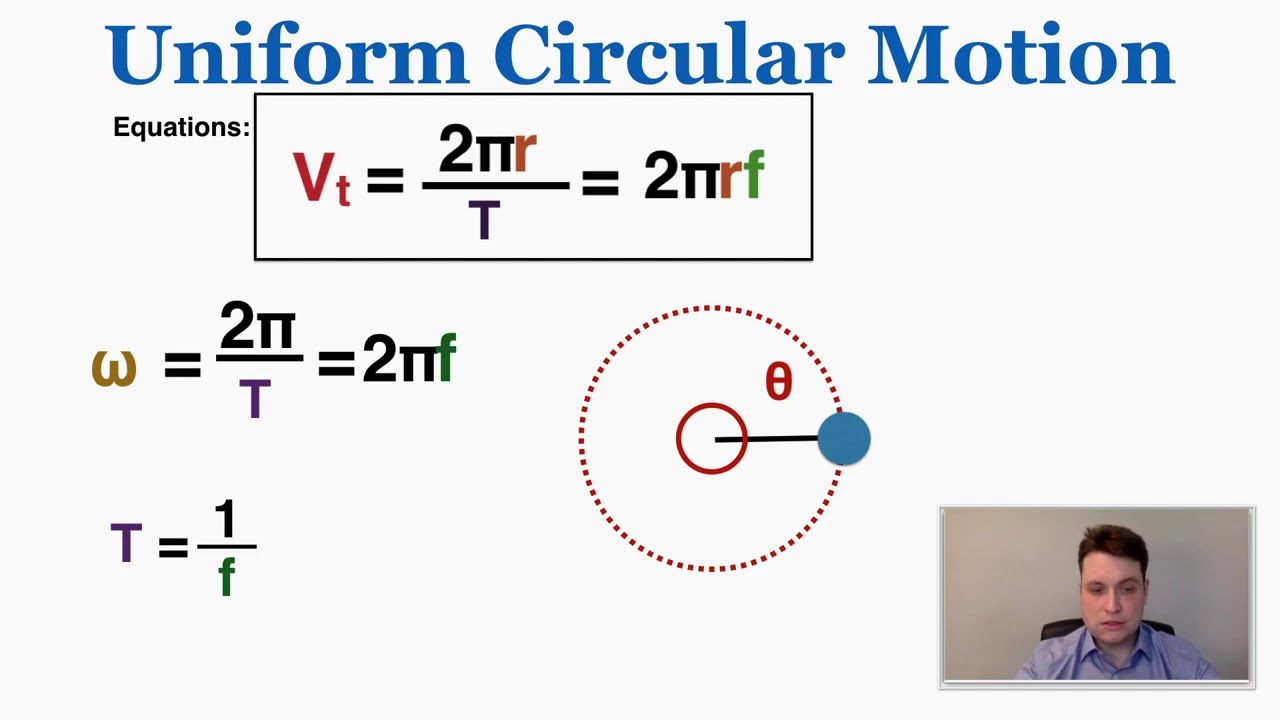
Uniform Circular Motion - IB Physics

Relating angular and regular motion variables | Physics | Khan Academy

Rotational Motion Physics, Basic Introduction, Angular Velocity & Tangential Acceleration

Rotational Motion: An Explanation, Angular Displacement, Velocity and Acceleration
5.0 / 5 (0 votes)
Thanks for rating: