Circular Motion: Acceleration (Angular, Tangential, Centripetal)

The Science Classroom
8 Mar 201408:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of acceleration in circular motion, highlighting three distinct types: angular, tangential, and centripetal acceleration. Angular acceleration, symbolized by alpha, is analogous to linear acceleration but pertains to changes in angular velocity (measured in radians per second). Tangential acceleration is derived from angular acceleration and the circle's radius, transforming angular motion into linear terms. Lastly, centripetal acceleration, always directed towards the circle's center, is calculated using a formula involving velocity and radius, reflecting the constant change in direction despite uniform speed in circular motion. The script illustrates these concepts with examples, such as spinning a globe and a plane's propeller, to clarify the calculations and applications of these accelerations.

Takeaways
  • πŸ”„ There are three types of acceleration in circular motion: angular acceleration, tangential acceleration, and centripetal acceleration.
  • πŸ“ Angular acceleration is directed outward from the center of the circle and is based on the change in angular velocity over time.
  • πŸŒ€ Angular velocity is measured in radians per second, which is a measure of the angle through which an object rotates.
  • ⏱️ The formula for angular acceleration is similar to linear acceleration, using the Greek letter alpha (Ξ±) and angular velocity (Ο‰).
  • 🌍 An example problem involves spinning a globe, calculating the angular acceleration when the speed changes from 2.5 to 3 radians per second over 0.2 seconds.
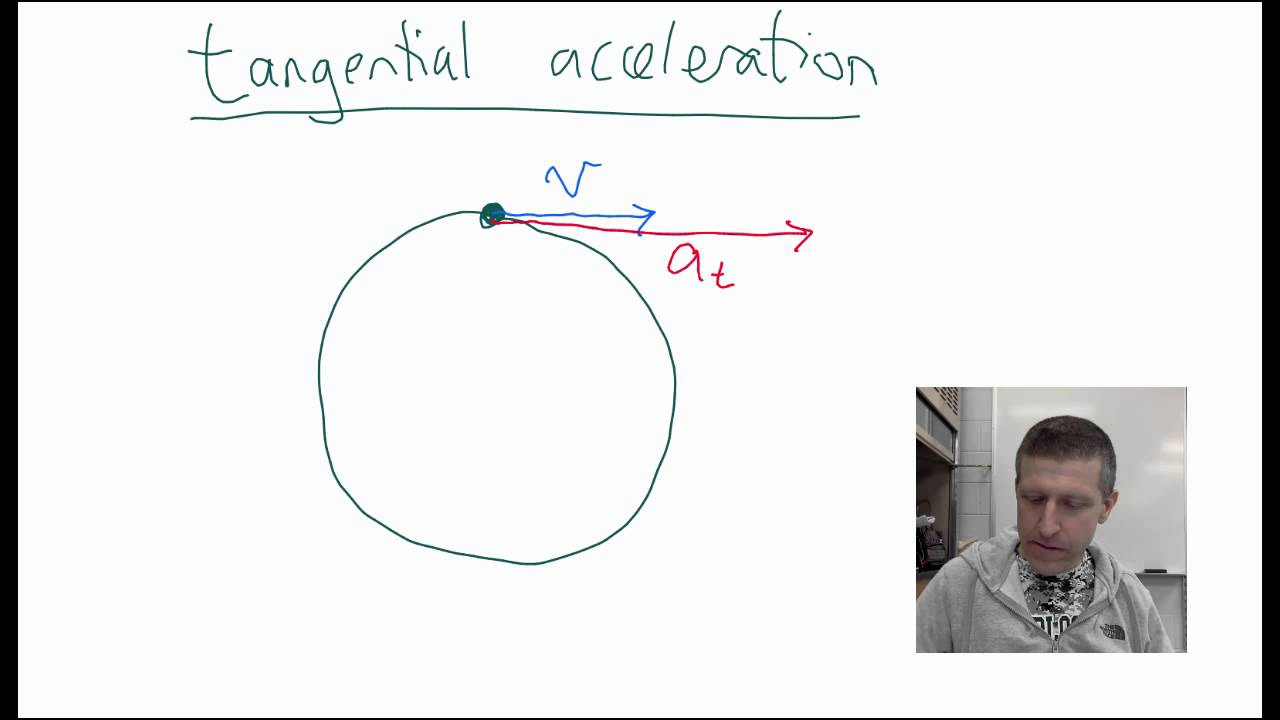
  • πŸ“ Tangential acceleration is directed tangent to the circle and is calculated by multiplying angular acceleration by the radius of the circle.
  • πŸ›€οΈ The radius of the circle is crucial for converting angular motion into a linear version, affecting tangential acceleration.
  • πŸ›¬ Centripetal acceleration always points toward the center of the circle and is derived from calculus, with the formula a_c = v^2 / r.
  • πŸ”„ Centripetal acceleration occurs in uniform circular motion where the speed is constant but the direction of velocity is continuously changing.
  • ✈️ A practical example of centripetal acceleration is given by calculating the acceleration at the tips of a spinning propeller with a known radius and speed.
  • πŸ“š The script explains the concept of acceleration in circular motion with clear examples and emphasizes the importance of understanding the direction and calculation of each type of acceleration.
Q & A

  • What are the three types of acceleration associated with circular motion?

    -The three types of acceleration associated with circular motion are angular acceleration, tangential acceleration, and centripetal acceleration.

  • How is angular acceleration defined in relation to linear acceleration?

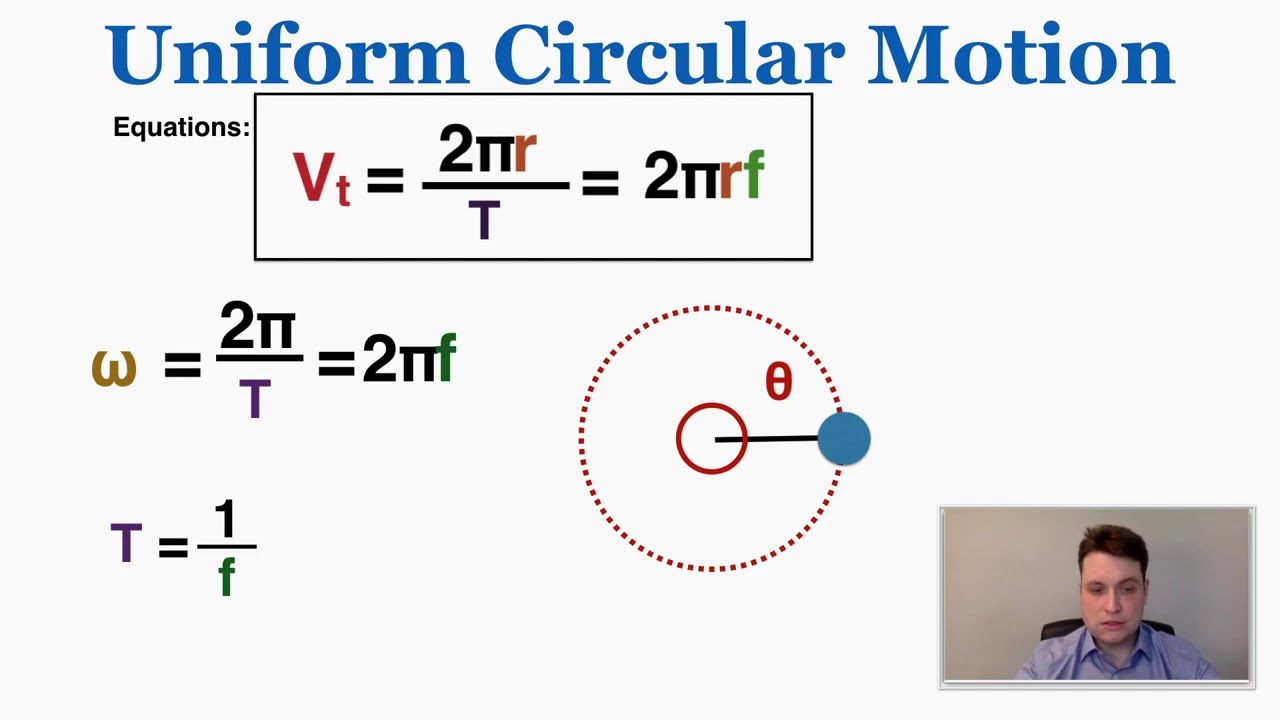
    -Angular acceleration is defined similarly to linear acceleration, which is the rate at which velocity changes. Instead of using 'a' for linear acceleration, 'Ξ±' (alpha) is used for angular acceleration, and instead of linear velocity, angular velocity (Ο‰) is used.

  • What is the SI unit used to measure angular velocity?

    -The SI unit used to measure angular velocity is radians per second.

  • How can you calculate angular acceleration using the given information in the script?

    -You can calculate angular acceleration by using the formula Ξ± = (Ο‰_final - Ο‰_initial) / T, where Ο‰_final is the final angular velocity, Ο‰_initial is the initial angular velocity, and T is the time taken for the change.

  • What is the formula for tangential acceleration in terms of angular acceleration?

    -The formula for tangential acceleration is a_tangential = R * Ξ±, where R is the radius of the circle and Ξ± is the angular acceleration.

  • How does the radius of a circle affect tangential acceleration?

    -The radius of a circle affects tangential acceleration by being multiplied with the angular acceleration, thus changing the angular motion into a linear version.

  • What is the direction of centripetal acceleration?

    -Centripetal acceleration always points directly towards the center of the circle.

  • Why is calculus needed to derive the equation for centripetal acceleration?

    -Calculus is needed to derive the equation for centripetal acceleration because it involves the rate of change of velocity in a circular path, which requires integration or differentiation to solve.

  • How is the direction of centripetal acceleration related to the velocity vectors?

    -The direction of centripetal acceleration is towards the center of the circle and is determined by the vector difference between the final and initial tangential velocities, which points inward.

  • What is the significance of centripetal acceleration in uniform circular motion?

    -In uniform circular motion, even though the speed of the object remains constant, the direction of the velocity changes continuously, which means there is a centripetal acceleration acting towards the center of the circle to change the direction of the velocity vector.

  • How can you calculate the centripetal acceleration of a spinning propeller blade?

    -You can calculate the centripetal acceleration of a spinning propeller blade using the formula a_centripetal = v^2 / R, where v is the linear speed of the blade and R is the radius of the circle formed by the blade's motion.

Outlines
00:00
πŸ”„ Angular and Tangential Acceleration in Circular Motion

This paragraph introduces the concept of acceleration in circular motion, focusing on angular and tangential acceleration. Angular acceleration (Ξ±) is described as the rate of change of angular velocity (Ο‰), measured in radians per second squared, and is analogous to linear acceleration but uses angular velocity instead of linear velocity. The equation for angular acceleration is Δω/T, where Δω is the change in angular velocity and T is time. An example problem is presented where a globe is spun at 2.5 radians per second and then accelerated to 3 radians per second in 0.2 seconds, resulting in an angular acceleration of 2.5 radians per second squared. Tangential acceleration is then discussed as the acceleration directed tangent to the circle, which is derived by multiplying angular acceleration by the radius of the circle. Using the same globe example with a radius of 0.35 meters, the tangential acceleration is calculated to be 0.88 meters per second squared.

05:02
πŸŒ€ Centripetal Acceleration in Uniform Circular Motion

The second paragraph delves into centripetal acceleration, which always points towards the center of the circle. Centripetal acceleration is a result of uniform circular motion where the speed is constant, but the direction of velocity changes continuously, leading to a changing velocity vector. The equation for centripetal acceleration is derived from calculus and is not explicitly shown here, but it is based on the difference between final and initial tangential velocities (Ξ”V = V_final - V_initial). The vector addition of these velocities results in a vector pointing towards the center of the circle. An example is given involving a plane propeller with a tip speed of 350 meters per second and a radius of 3.5 meters, which calculates to a centripetal acceleration of 35,000 meters per second squared. The paragraph emphasizes that centripetal acceleration is crucial for understanding the motion of objects in circular paths, such as the blades of a spinning propeller.

Mindmap
Keywords
πŸ’‘Acceleration
Acceleration is defined as the rate at which velocity changes. It is a fundamental concept in physics that describes how quickly an object's speed or direction changes over time. In the context of the video, acceleration is discussed in relation to circular motion, where different types of accelerations are at play, such as angular, tangential, and centripetal acceleration.
πŸ’‘Circular Motion
Circular motion refers to the movement of an object around a circular path. It is a type of motion where the object's trajectory is a circle. The video script delves into the different accelerations that occur when objects are in circular motion, emphasizing that acceleration is not just about speed but also about changes in direction.
πŸ’‘Angular Acceleration
Angular acceleration, symbolized by the Greek letter alpha (Ξ±), is the rate at which an object's angular velocity changes over time. It is directly related to linear acceleration but applies to rotational motion. The script explains that angular acceleration is directed outward from the center of the circle and uses the example of spinning a globe to illustrate its calculation.
πŸ’‘Tangential Acceleration
Tangential acceleration is the component of acceleration that is directed along the tangent to the circular path of an object in motion. It is derived from angular acceleration and the radius of the circle. The video script provides a formula and an example of calculating tangential acceleration using the radius of a globe and its change in angular velocity.
πŸ’‘Centripetal Acceleration
Centripetal acceleration is the acceleration directed towards the center of the circular path that an object is following. It is responsible for keeping the object in circular motion and is calculated using the formula a_c = v^2 / r, where 'v' is the tangential velocity and 'r' is the radius of the circle. The script explains this concept with an example of a propeller blade and emphasizes that it is based on uniform circular motion where the speed is constant but the direction changes.
πŸ’‘Angular Velocity
Angular velocity, represented by the Greek letter Omega (Ξ©), measures how fast an object is rotating or changing its angle over time. It is typically measured in radians per second. In the video, angular velocity is used to calculate angular acceleration and is central to understanding the dynamics of circular motion.
πŸ’‘Radius
The radius is the distance from the center of a circle to any point on the circumference. In the context of circular motion, the radius is a key factor in calculating both tangential and centripetal accelerations. The script uses the radius of a globe and a propeller to demonstrate how it affects the accelerations in different scenarios.
πŸ’‘Uniform Circular Motion
Uniform circular motion is a specific type of circular motion where the speed of the object remains constant, even though its direction is continually changing. The video script mentions this concept when discussing centripetal acceleration, noting that even though the speed is constant, the changing direction results in a centripetal acceleration towards the center of the circle.
πŸ’‘Tangent
A tangent to a circle is a straight line that touches the circle at exactly one point, the tangent point. In the context of the video, tangential acceleration is named for its direction along the tangent to the circle at the point of contact. This concept is crucial for understanding how objects accelerate as they move along a circular path.
πŸ’‘Linear Acceleration
Linear acceleration refers to the rate at which an object's velocity changes in a straight line. It is the basis for understanding angular acceleration, as the script explains that angular acceleration is calculated similarly to linear acceleration but involves changes in angular velocity instead of linear velocity.
Highlights

Introduction to three types of acceleration in circular motion: angular, tangential, and centripetal acceleration.

Angular acceleration is directed outward from the center of the circle, similar to linear acceleration but with angular velocity.

Angular acceleration formula is presented as alpha equals change in angular velocity over time.

SI units for angular velocity are radians per second, a measure of the angle of change.

Example problem: calculating angular acceleration of a spinning globe with given initial and final angular velocities and time.

Tangential acceleration is directed tangent to the circle and is derived from angular acceleration multiplied by the radius.

Explanation of the relationship between angular acceleration and tangential acceleration using radius.

Example calculation of tangential acceleration for a globe with a given radius.

Centripetal acceleration always points towards the center of the circle and is distinct from tangential and angular acceleration.

Centripetal acceleration is based on uniform circular motion where speed is constant but direction changes.

Centripetal acceleration formula is derived using calculus and is presented as a = (v^2)/r.

Illustration of how centripetal acceleration is calculated by considering the change in velocity direction.

Example problem involving calculating centripetal acceleration for a spinning propeller blade.

Explanation of the importance of direction change in circular motion for understanding centripetal acceleration.

Final calculation of centripetal acceleration for the propeller blade with given speed and radius.

Summary of the key concepts of acceleration in circular motion and their practical applications.

Transcripts

Browse More Related Video

Rotational Motion: An Explanation, Angular Displacement, Velocity and Acceleration

Relating angular and regular motion variables | Physics | Khan Academy

AP Physics C: Rotational Kinematics Review (Mechanics)

Uniform Circular Motion Class 11

1.6 - Tangential Acceleration

Uniform Circular Motion - IB Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Circular MotionAcceleration TypesAngular AccelerationTangential AccelerationCentripetal AccelerationPhysics ConceptsEducational ContentMotion AnalysisVelocity ChangeRadial Forces