Uniform Circular Motion - IB Physics
TLDRThis educational lecture delves into the principles of uniform circular motion, explaining the necessity of a centripetal force and a velocity perpendicular to it for an object to maintain circular motion. It clarifies misconceptions about centripetal force and acceleration, emphasizing their roles in changing the direction of velocity, not its magnitude. The lecture introduces key terms such as tangential velocity, centripetal acceleration, period, frequency, and angular velocity, illustrating their relationships with equations and examples. Practical problems, like calculating the force of friction on a car turning and the Earth's orbital speed and acceleration, demonstrate the application of these concepts.
Takeaways
- 🌀 Uniform circular motion requires a net force that is constant and always points toward the center of the circle.
- 🚀 Newton's First Law states that an object will maintain its velocity unless acted upon by an external force, which is crucial for initiating circular motion.
- 📉 Centripetal force is not a unique type of force but rather the net force directed towards the center of the circular path, which can be composed of various forces.
- 📐 The centripetal acceleration is always directed towards the center of the circle, changing the direction of the velocity, not its magnitude.
- 🔄 The tangential velocity is the rate at which an object moves along the circumference of the circle, measured in meters per second.
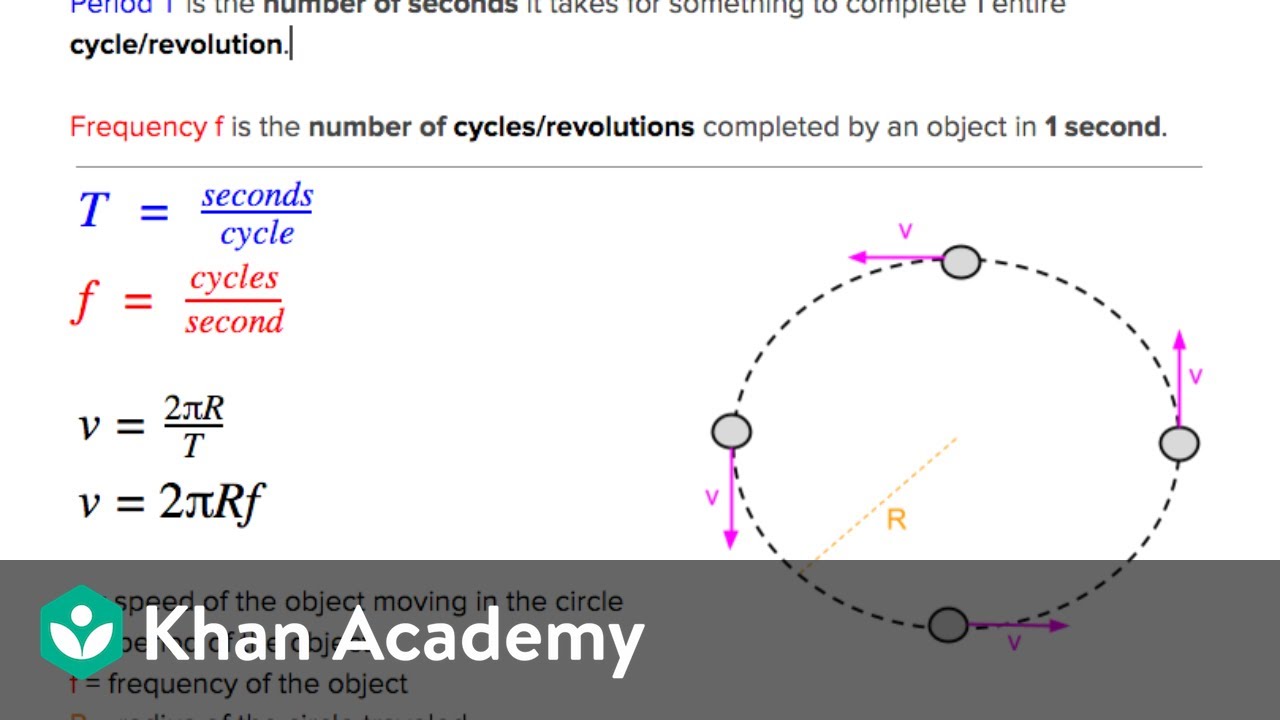
- ⏱ The period of circular motion is the time taken for one complete revolution around the circle, measured in seconds.
- 🔢 Frequency in circular motion is the number of complete cycles that occur in one second and is measured in Hertz (Hz).
- 🔄 Angular velocity measures the rate of change of angle over time and is expressed in radians per second.
- 🔗 There is a direct relationship between tangential velocity, angular velocity, and the radius of the circle: tangential velocity equals angular velocity times the radius.
- 📚 The equations for tangential velocity (v = 2πR/T or v = 2πR * f), angular velocity (ω = 2π/T or ω = 2πf), and centripetal acceleration (a = v^2/R) are fundamental for solving circular motion problems.
- 📘 Centripetal force can be calculated using the formula F = m * a, where m is the mass of the object and a is the centripetal acceleration.
Q & A
What is uniform circular motion?
-Uniform circular motion is the motion of an object moving in a circle at a constant speed. It requires a constant net force, known as centripetal force, always pointing toward the center of the circle to maintain the motion.
Why can't an object continue in uniform circular motion without an applied force?
-According to Newton's First Law, an object will maintain its velocity unless acted upon by a force. Without a force, the object would continue in a straight line at a constant speed, rather than moving in a circular path.
What are the two requirements for an object to undergo circular motion?
-The two requirements are: 1) The net force must be constant and always point toward the center of the circular path, and 2) There must be a constant velocity at a 90-degree angle to the net force.
What is meant by the term 'centripetal force' in the context of circular motion?
-Centripetal force is the net force acting on an object that is moving in a circle. It always points toward the center of the motion and is measured in Newtons.
How is tangential velocity different from centripetal acceleration?
-Tangential velocity is the speed at which an object moves along the circumference of the circle, measured in meters per second. Centripetal acceleration, on the other hand, is the acceleration directed towards the center of the circle, and it changes the direction of the velocity, not its magnitude.
What is the relationship between period and frequency in circular motion?
-The period is the time it takes for an object to complete one full cycle, measured in seconds, while frequency is the number of cycles completed in one second, measured in Hertz (Hz). The period is equal to one over the frequency, and vice versa.
What is angular velocity, and how is it different from tangential velocity?
-Angular velocity is the rate of change of the angle with respect to time, measured in radians per second. It represents how many radians an object rotates around a circle in a given time. Tangential velocity, in contrast, is the actual speed of the object along the circular path in meters per second.
Why does centripetal acceleration not increase the speed of an object in circular motion?
-Centripetal acceleration is responsible for changing the direction of the velocity vector, not its magnitude. It keeps the object moving in a circular path by constantly redirecting the velocity vector towards the center of the circle.
Can you provide an example of how to calculate the centripetal force needed for a car to turn a corner?
-To calculate the centripetal force for a car turning a corner, you would use the formula: Centripetal Force = Mass × (Tangential Velocity)^2 / Radius. Given the mass of the car, the radius of the turn, and the tangential velocity, you can solve for the centripetal force.
How can you determine the Earth's tangential velocity and centripetal acceleration as it orbits the Sun?
-To determine Earth's tangential velocity, you can use the formula: Tangential Velocity = 2π × Radius / Period, where the radius is the average distance from Earth to the Sun and the period is one year in seconds. The centripetal acceleration can then be calculated using the formula: Centripetal Acceleration = (Tangential Velocity)^2 / Radius.
Outlines
🌌 Introduction to Uniform Circular Motion
The script begins with an introduction to uniform circular motion, explaining that an object in circular motion requires a centripetal force constantly directed toward the center of the circle. It uses the analogy of a cart moving in a circle with a rope providing the necessary force. The importance of maintaining a constant velocity perpendicular to the force is emphasized. Key terms such as centripetal force, tangential velocity, radius, and centripetal acceleration are defined, with the clarification that centripetal force is not a unique type of force but rather the net force directed toward the center. The misconception that centripetal acceleration increases the speed of the object is corrected, explaining that it only changes the direction of the velocity.
📚 Understanding Circular Motion Concepts and Equations
This section delves deeper into the concepts of circular motion, discussing the relationship between centripetal force, acceleration, velocity, and the object's path. It clarifies that while the velocity of an object in circular motion is always tangential to the path, the acceleration (centripetal acceleration) is always directed toward the center. The script introduces the terms 'period' and 'frequency', explaining that the period is the time taken for one complete cycle, and frequency is the number of cycles per second, with a mathematical relationship between the two. Angular velocity is introduced as the rate of change of angle over time, measured in radians per second, and is contrasted with tangential velocity, which is the actual speed of the object in meters per second. The summary includes equations for tangential velocity, angular velocity, centripetal acceleration, and centripetal force, highlighting their interdependencies.
🚗 Applying Circular Motion Principles to Real-World Problems
The final paragraph presents two example problems to illustrate the application of circular motion principles. The first problem involves calculating the force of friction needed for a 1000 kg car to turn a corner with a radius of curvature of 30 meters in 4 seconds. The solution involves determining the car's tangential velocity and then using it to calculate the centripetal force, which is provided by the friction between the car's wheels and the road. The second problem asks for the Earth's tangential velocity and centripetal acceleration as it orbits the Sun, given the distance between the Earth and the Sun and understanding that the period of Earth's orbit is one year. The solution process involves converting the period into seconds and using the known radius of the Earth's orbit to calculate the Earth's velocity and acceleration towards the Sun. These examples demonstrate the practical use of the equations introduced earlier in the script.
Mindmap
Keywords
💡Uniform Circular Motion
💡Centripetal Force
💡Tangential Velocity
💡Radius
💡Centripetal Acceleration
💡Newton's First Law
💡Period
💡Frequency
💡Angular Velocity
💡Centripetal Force Misconception
💡Tangential Acceleration Misconception
Highlights
Uniform circular motion requires a constant net force pointing toward the center of the circle.
Newton's First Law explains why an object in motion continues with its velocity unless acted upon by a force.
Two requirements for circular motion: constant net force towards the center and constant velocity at a 90-degree angle to the net force.
Centripetal force is the net force on an object moving in a circle, always pointing toward the center of motion.
Tangential velocity is the distance the object moves around the circle over time, measured in meters per second.
Centripetal acceleration is the acceleration towards the center of the circle, always pointing toward the center due to the net force.
Centripetal force is not a unique type of force but the net total force pointing toward the center of motion.
Acceleration in circular motion changes the direction of velocity, not its magnitude.
Period is the time taken for one complete cycle in circular motion, measured in seconds.
Frequency is the number of cycles completed in one second, measured in Hertz (Hz).
The relationship between period and frequency: period equals one over the frequency.
Angular velocity is the change in angle over time, measured in radians per second.
Tangential velocity is different from angular velocity; the former is speed in meters per second, the latter is rate of rotation in radians per second.
Equation for tangential velocity: Vt = 2πR/T, where Vt is tangential velocity, R is radius, and T is period.
Equation for angular velocity: ω = 2π/T, where ω is angular velocity.
Equation relating tangential velocity and angular velocity: Vt = ωR.
Centripetal acceleration equation: ac = Vt^2/R, where ac is centripetal acceleration.
Centripetal force equation: Fc = m(Vt^2/R), where Fc is centripetal force and m is mass.
Example problem: Calculating the force of friction needed for a car to turn a corner in circular motion.
Example problem: Determining Earth's tangential velocity and centripetal acceleration in its orbit around the Sun.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: