Lec 16 | MIT 18.01 Single Variable Calculus, Fall 2007
TLDRThe script from an MIT OpenCourseWare lecture introduces the concept of ordinary differential equations, focusing on the separation of variables technique. The professor corrects a previous error regarding the formula for c_1 - c_2 and proceeds to solve several examples, including the ground state of a harmonic oscillator and geometric problems involving curves with specific slope properties. The lecture emphasizes the importance of understanding the relationship between derivatives and the original function, highlighting the method's application in various scenarios and the need to consider special cases and the implications of the solutions.
Takeaways
- 📚 The lecture is part of MIT OpenCourseWare, which provides free educational resources and accepts donations to continue its mission.
- 🔍 A correction was made to a previous lecture's formula, emphasizing the importance of accuracy in mathematical communication.
- 📈 The professor introduces differential equations as a key topic, highlighting their importance in various fields including quantum mechanics.
- 🔑 The first technique discussed for solving differential equations is separation of variables, which is applicable when the equation can be expressed in the form f(x)g(y).
- 📝 The method of separation of variables involves dividing by g(y) and multiplying by dx, which allows for the integration of differentials.
- 🧩 The solution to the differential equation dy/dx = -xy is derived, showcasing the process of solving such equations step by step.
- 📉 The solution to the equation is related to the normal distribution, which has applications in probability and quantum mechanics.
- 🔍 The professor emphasizes the importance of checking solutions to differential equations to ensure they satisfy the original equation.
- 📚 The lecture provides a general method for solving differential equations and discusses the subtleties involved, such as dealing with constants and implicit equations.
- 🔄 The professor warns about the potential pitfalls when solving differential equations, such as missing solutions or issues at points where the equation is undefined.
- 📈 The lecture concludes with a review of the material and a preview of what will be on the test, focusing on the relationship between derivatives and the original function.
Q & A
What is the main topic introduced in the script's last day of the second unit?
-The main topic introduced is differential equations, specifically focusing on a technique that fits with what has been discussed, which is differentials.
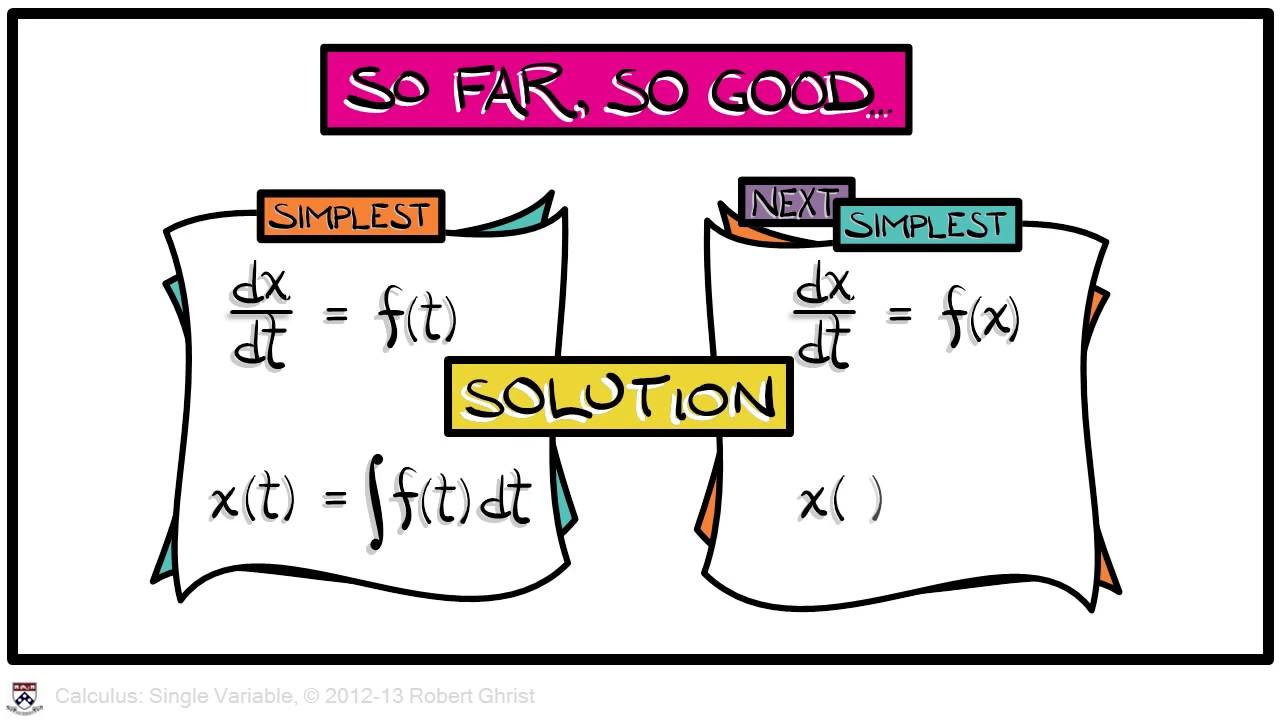
What is the simplest kind of differential equation mentioned in the script?
-The simplest kind of differential equation mentioned is when the rate of change of x with respect to y is equal to some function f(x).
What is the method used to solve the differential equation dy/dx = -xy?
-The method used to solve the differential equation dy/dx = -xy is separation of variables, followed by integrating the separated differentials.
What is the significance of the differential equation dy/dx + x*y = 0 in quantum mechanics?
-The differential equation dy/dx + x*y = 0 is significant in quantum mechanics because it governs the ground state of the harmonic oscillator and is studied for its simple solutions.
How does the script describe the process of solving the differential equation with the annihilation operator?
-The script describes the process as involving rewriting the equation, separating out the differentials, and then using Leibniz's notation to integrate these differentials to find the antiderivatives.
What is the general form of the solution to the differential equation dy/dx = -xy?
-The general form of the solution is y = A * e^(-x^2 / 2), where A is any constant, which can be positive, negative, or zero.
What is the method of separation of variables and when does it work?
-The method of separation of variables is used to solve differential equations of the form f(x) * g(y). It involves dividing by g(y) and multiplying by dx to separate the variables and then antidifferentiating both sides.
Why is it important to consider the case y = 0 in the solutions of the differential equations?
-It is important to consider the case y = 0 because it represents a solution to the problem, even though it may be a trivial or uninteresting one. It is also necessary to ensure that all possible solutions are accounted for.
How does the script handle the issue of constants in antiderivatives?
-The script explains that while it is common to introduce an arbitrary constant when antidifferentiating, it is superfluous to have two arbitrary constants because they can always be combined into one.
What is the geometric interpretation of the differential equation dy/dx = 2y/x?
-The geometric interpretation is that the slope of the tangent line to a curve is twice the slope of the ray from the origin to a point on the curve.
What is the implicit solution to the differential equation dy/dx = -x/(2y) and what does it represent geometrically?
-The implicit solution is x^2 / 2 + y^2 = c, which represents a family of ellipses with different sizes, where c is a constant representing the square of the ellipse's semi-major axis.
Why is it necessary to be cautious when considering the solutions to the differential equations presented in the script?
-It is necessary to be cautious because not all constants may work in the solutions, and there may be special points like x = 0 where the solution is not defined or the slope becomes infinite, which requires careful interpretation.
What is the main theme of the unit on ordinary differential equations according to the script?
-The main theme is that information about the derivative, and sometimes the second derivative, can provide information about the function itself, which is the essence of working with ordinary differential equations.
Outlines
📚 Introduction to Differential Equations and Corrections
The professor begins by addressing a correction made to a previous formula, emphasizing the importance of accuracy in mathematical communication. They then introduce the topic of differential equations, highlighting the relevance of this subject to various fields, including quantum mechanics. The focus is on a specific type of differential equation where the rate of change of x with respect to y is equal to a function f(x). The professor simplifies the solution approach by suggesting that antiderivatives, specifically through substitution or advanced guessing, are sufficient for the scope of the class. The session concludes with an introduction to a simple yet significant differential equation involving the annihilation operator, which is foundational in quantum mechanics.
🔍 Solving the Harmonic Oscillator Differential Equation
This paragraph delves into solving a differential equation that describes the ground state of a harmonic oscillator. The equation involves both x and y, making it more complex than previous examples. The professor employs a clever technique involving differentials to separate the variables, allowing for the equation to be solved by integrating both sides. The solution process involves taking antiderivatives, leading to an expression involving the natural logarithm and a quadratic function of x. The final solution is expressed in terms of an exponential function, which is recognized as the normal distribution, a fundamental concept in probability and quantum mechanics. The professor also ensures that the solution is checked for accuracy by differentiating it back and verifying that it satisfies the original equation.
📘 General Method of Separation of Variables in Differential Equations
The professor outlines the general method for solving differential equations when they can be expressed in the form of f(x)g(y). This method, known as separation of variables, involves dividing by g(y) and multiplying by dx, effectively separating the differentials and allowing for integration of both sides. The process results in an implicit equation that defines y in terms of x, which can sometimes be converted into an explicit equation. The professor also discusses the handling of constants and the importance of considering both positive and negative values for y, as well as the special case when y equals zero. The commentary highlights the importance of understanding the underlying concepts and the limitations of the method, such as the exclusion of certain solutions when division by a variable is involved.
📐 Differential Equations with Geometric Interpretations
The script transitions into using differential equations to solve geometric problems. The first example involves finding a curve where the slope of the tangent line at any point is twice the slope of the line from the origin to that point on the curve. The differential equation representing this relationship is derived and solved using the separation of variables technique. The solution is an implicit equation that describes a family of curves, which are then exponentiated to find the explicit form of the solution. The professor also addresses the importance of considering the implications of the solution, such as the behavior of the curves for positive and negative values of y, and the exclusion of the a = 0 case due to the division by y in the solution process.
📉 Exploring the Properties of the Solution and Implicit Equations
This paragraph further explores the properties of the solution to the geometric problem presented earlier. The professor discusses the importance of checking the solution to ensure it satisfies the original differential equation and addresses the issue of the solution being undefined at x = 0. They explain that the rate of change is undefined at this point, which means that knowing the value and the rate of change at x = 0 does not uniquely specify the function. The professor warns that the function could potentially transition from one branch to another across x = 0, suggesting that the solution should be visualized as rays emanating from the origin rather than complete parabolas.
📈 Solving for Perpendicular Curves to Parabolas
The professor presents a fourth example involving curves perpendicular to parabolas. They derive the differential equation for the slope of these curves, which is the negative reciprocal of the slope of the tangent to the parabola. The differential equation is solved using the separation of variables technique, resulting in an implicit equation that describes a family of ellipses. The professor notes that not all constants are valid in this solution and only positive values of the constant are permissible. The explicit solutions are also provided, revealing that the ellipses are only partially valid solutions due to the vertical slope at y = 0, where the solution stops. The professor emphasizes the importance of being cautious with these solutions and understanding their geometric implications.
📝 Review and Conclusion of Ordinary Differential Equations
In the final paragraph, the professor reviews the material covered in the lesson and provides guidance for an upcoming test. They reiterate the main theme of the unit, which is that information about the derivative, and sometimes the second derivative, can provide information about the function itself. This concept is central to the study of ordinary differential equations. The professor encourages students to review the material and to look at previous tests to understand the types of problems that will be asked. They conclude by emphasizing the importance of this foundational knowledge in the study of differential equations.
Mindmap
Keywords
💡Creative Commons license
💡MIT OpenCourseWare
💡Differentiation
💡Differential equations
💡Separation of variables
💡Antiderivatives
💡Annihilation operator
💡Harmonic oscillator
💡Normal distribution
💡Implicit equation
💡General solution
Highlights
The professor corrects a previous misprint regarding the formula for c_1 - c_2, stating that it should be -1/2 instead of +1/2.
Introduction to differential equations as a new topic in the course.
Explanation of the simplest type of differential equation where the rate of change of x with respect to y is a function of x.
Discussion of solving differential equations using the technique of differentials and antiderivatives.
Introduction of the annihilation operator from quantum mechanics and its role in solving differential equations.
Detailed step-by-step solution of the differential equation dy/dx + x*y = 0 using separation of variables and integration.
Emphasis on the importance of separation of variables in solving differential equations.
Explanation of the general method of separation of variables and its application.
Clarification on the role of arbitrary constants in solutions to differential equations.
Discussion on the general solution of differential equations and its family of functions.
Introduction of geometric interpretation of differential equations through an example involving curves and their tangents.
Step-by-step solution of a geometry-based differential equation involving parabolas and their slopes.
Explanation of how to deal with implicit solutions and the importance of careful handling of constants and variables.
Example of solving a differential equation involving curves perpendicular to given parabolas.
Final remarks on the review of topics covered and instructions for the upcoming test, highlighting the importance of understanding the relationship between derivatives and functions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: