Lec 1 | MIT 18.01 Single Variable Calculus, Fall 2007

MIT OpenCourseWare

18 Aug 200951:32

EducationalLearning

32 Likes 10 Comments

TLDRIn this MIT OpenCourseWare lecture, Professor David Jerison introduces Unit One on differentiation, focusing on the geometric interpretation of derivatives. He explains the concept of a derivative as the slope of the tangent line to a curve at a given point. The lecture covers the visual and analytical process of finding tangent lines, introduces various notations for derivatives, and demonstrates the calculation of derivatives for basic functions such as 1/x and x^n. The professor also discusses the importance of derivatives in various fields and the challenges of handling multiple variables in calculus. The session includes examples and a word problem involving the area of triangles formed by the tangents to the hyperbola y=1/x.

Takeaways

📚 The lecture introduces Unit One on differentiation, emphasizing the concept of a derivative and its importance across various disciplines.
📈 The geometric interpretation of derivatives is the primary focus, starting with the problem of finding the tangent line to a graph at a specific point.
🔍 The professor illustrates the tangent line graphically and discusses the challenge of determining it analytically, as opposed to the intuitive geometric approach.
📉 The derivative is defined as the slope of the tangent line to the graph of a function at a given point, denoted as f'(x_0).
📚 The lecture introduces the concept of secant lines and their role in approximating the slope of the tangent line through the limit process as the secant line's second point approaches the first.
🔢 The difference quotient is highlighted as the key formula for calculating the derivative, involving the change in function value (delta f) over the change in x (delta x).
📝 An example is worked through to demonstrate the calculation of the derivative of the function f(x) = 1/x, resulting in f'(x_0) = -1/x_0^2.
📉 The graph of the function 1/x is analyzed to verify the plausibility of the derived derivative, noting the negative slope and its behavior as x approaches infinity.
🤔 The professor addresses common misconceptions about the difficulty of calculus, attributing it to the complexity of word problems that integrate various mathematical concepts.
📐 A word problem involving the area of triangles formed by the axes and a tangent to the function y = 1/x is presented, with calculus used to find the tangent line equation and geometry to calculate the area.
📘 The lecture concludes with a discussion on various notations for derivatives, including Newton's f prime notation and Leibniz's df/dx and dy/dx notations.

Q & A

What is the main topic of Unit One in the course?
-The main topic of Unit One is differentiation, specifically understanding what a derivative is from various perspectives including geometric and physical interpretations.
Why are derivatives considered fundamental in science and engineering?
-Derivatives are fundamental because of their importance to all measurements, which means they have applications in science, engineering, economics, political science, and many other fields.
What is the geometric interpretation of derivatives?
-The geometric interpretation of derivatives involves finding the slope of the tangent line to a graph of a function at a specific point (x_0, y_0).
How does the professor describe the process of drawing a tangent line to a curve?
-The professor describes the process as a geometric problem where one visualizes the tangent line and figures it out mentally. The goal is to develop an analytical method that can replicate this visualization.
What is the equation of a tangent line to a curve at a given point?
-The equation of a tangent line is given by y - y_0 = m(x - x_0), where m is the slope of the tangent line and (x_0, y_0) is the point on the curve.
What is the definition of the derivative of a function at a specific point?
-The derivative of a function f at a point x_0, denoted as f'(x_0), is defined as the slope of the tangent line to the graph of y = f(x) at the point P.
How does the professor explain the concept of a secant line in the context of finding a tangent line?
-The professor explains that the tangent line is the limit of secant lines as the second point Q approaches the first point P. As Q gets closer to P, the slope of the secant line approaches the slope of the tangent line.
What is the difference quotient and why is it important?
-The difference quotient is the expression (f(x_0 + delta x) - f(x_0))/delta x. It is important because it is used to calculate the derivative of a function at a point x_0 by taking the limit as delta x approaches 0.
Can you provide an example of a function and its derivative as discussed in the script?
-An example given in the script is the function f(x) = 1/x. The derivative of this function at a point x_0 is found to be f'(x_0) = -1/x_0^2.
What is the significance of the function y = 1/x in the context of the area of triangles problem?
-The function y = 1/x is significant because it is used to find the areas of triangles enclosed by the axes and the tangent to the function in the first quadrant.
How does the professor use symmetry to find the y-intercept of the tangent line to the function y = 1/x?
-The professor uses the symmetry of the situation, which involves a kind of mirror symmetry around the diagonal, exchanging the roles of x and y. This symmetry allows for the y-intercept to be found as 2y_0 without direct calculation.
What is the result of the area calculation for the triangles enclosed by the axes and the tangent to y = 1/x?
-The result of the area calculation for the triangles is 2, which is a constant and does not depend on the specific values of x_0 and y_0.
What are some alternative notations for the derivative mentioned in the script?
-Some alternative notations for the derivative mentioned in the script include delta y (or delta f), f', df/dx, dy/dx, and d/dx of f or y.
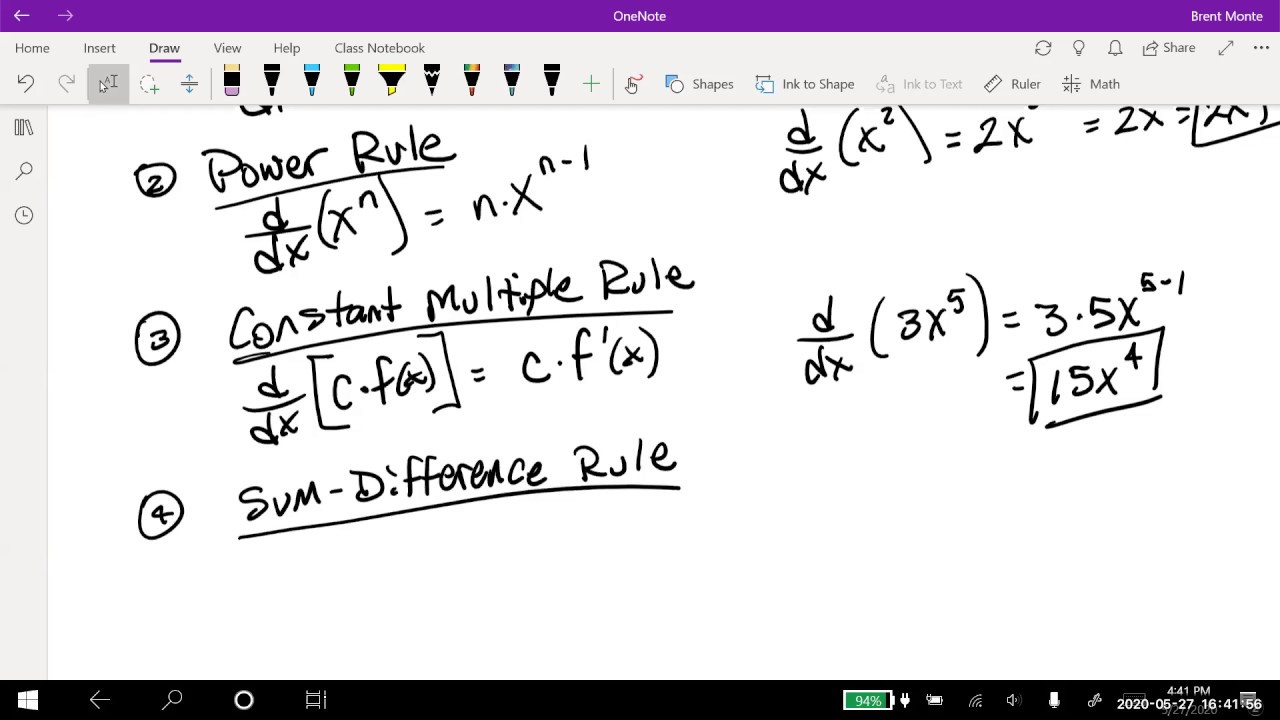
How does the professor explain the derivative of a function f(x) = x^n?
-The professor explains that the derivative of the function f(x) = x^n with respect to x is nx^(n-1), using the binomial theorem and considering the limit as delta x approaches 0.
What is the binomial theorem and how is it applied in the context of finding the derivative of x^n?
-The binomial theorem is a general formula that describes the expansion of powers of a binomial. In the context of finding the derivative of x^n, only the first two terms of the expansion are needed, and the rest are considered as higher order terms that can be ignored as delta x approaches 0.
How does the professor extend the concept of the derivative of x^n to polynomials?
-The professor extends the concept by showing that the derivative of a polynomial, such as x^3 + 5x^10, can be found by applying the rule nx^(n-1) to each term of the polynomial separately.

Outlines

00:00

📚 Introduction and Overview

The content is provided under a Creative Commons License. Support for MIT OpenCourseWare helps continue offering high-quality educational resources for free. The introduction welcomes students to Calculus 18.01, outlining the main topics including differentiation, geometric interpretation of derivatives, and the importance of derivatives in various fields like science, engineering, economics, and more. The professor explains the goal of understanding how to differentiate any function.

05:01

📐 Geometric Interpretation of Derivatives

The professor discusses the geometric problem of finding the tangent line to a graph at a point. They demonstrate graphing the function and drawing the tangent line, explaining that the goal is to figure out how to do this analytically. The tangent line is defined as having the equation y - y_0 = m(x - x_0), where m is the slope, also known as the derivative of the function at x_0.

10:01

🔍 Understanding Secant Lines and Limits

The professor explains the concept of a secant line, which connects two points on a curve, and how its slope approaches the slope of the tangent line as one point moves closer to the other. They introduce the limit notation to express this concept, showing how the slope of the tangent line is the limit of the slope of the secant lines as the distance between the points approaches zero.

15:05

📏 Calculating the Slope of the Tangent Line

The professor provides a detailed calculation of the derivative using the function 1/x as an example. They demonstrate how to simplify the difference quotient and take the limit as the change in x approaches zero to find the derivative. This example illustrates the process of finding the slope of the tangent line algebraically.

20:09

📊 Example: Derivative of 1/x

Using the example of the function 1/x, the professor calculates the derivative step-by-step, showing how the algebraic simplifications lead to the result f'(x_0) = -1/x_0^2. They verify the result by checking its plausibility against the graph, noting that the negative slope and its decreasing steepness as x_0 increases are consistent with the derivative.

25:10

📝 Word Problem: Area of Triangles

The professor introduces a word problem involving the geometry of finding the area of triangles formed by the tangent line to y = 1/x and the axes. They draw a picture to illustrate the problem and set up the necessary calculations, emphasizing that the calculus part involves finding the tangent line while the rest relies on geometry and algebra.

30:15

🔄 Symmetry in Calculus Problems

The professor discusses the use of symmetry to find the x- and y-intercepts of the tangent line. By leveraging the symmetry of the function y = 1/x, they simplify the problem and calculate the intercepts, demonstrating how this approach can make solving geometric problems easier.

35:17

💡 The Concept of Symmetry

Expanding on the idea of symmetry, the professor explains the symmetrical properties of the function y = 1/x and how switching the roles of x and y provides useful insights. They also highlight the potential confusion in dealing with multiple variables and the convenience of flexible variable notation in calculus.

40:22

🧮 Calculating the Area of the Triangle

The professor concludes the geometry problem by calculating the area of the triangle formed by the tangent line and the axes. They use the previously found intercepts to determine the base and height, ultimately showing that the area is always 2, regardless of the specific point on the function 1/x.

45:24

🔢 Introduction to Derivative Notations

The professor introduces different notations for derivatives, including Newton's notation (f') and Leibniz's notation (dy/dx), explaining their uses and the context in which they are applied. They emphasize the importance of understanding these notations for working with derivatives in various forms.

50:26

📈 Derivative of Power Functions

Using the function x^n as an example, the professor demonstrates how to calculate the derivative of power functions using the binomial theorem. They show the algebraic steps to simplify the difference quotient and find the derivative, emphasizing the importance of this process for understanding more complex derivatives.

Mindmap

Keywords

💡Derivative

The derivative is a fundamental concept in calculus that represents the rate at which a function changes with respect to its variable. In the video, the derivative is introduced as the slope of the tangent line to a curve at a given point, which is crucial for understanding how the function behaves locally. The geometric interpretation is emphasized, with the derivative being defined as the limit of the secant line's slope as the second point approaches the first point on the curve.

💡Geometric Interpretation

Geometric interpretation refers to understanding the concept of a derivative in terms of the geometry of a function's graph. The video spends a significant amount of time discussing this interpretation, specifically how the derivative at a point on a curve can be visualized as the slope of the tangent line at that point. This interpretation is key to solving problems related to the instantaneous rate of change.

💡Tangent Line

A tangent line is a straight line that touches a curve at a single point without crossing it. In the context of the video, the tangent line is crucial for defining the derivative. The professor illustrates the process of finding the tangent line to a function at a specific point and how it relates to the derivative, emphasizing the importance of the limit concept in this process.

💡Limit

The limit is a fundamental concept in calculus that describes the value that a function or sequence approaches as the input approaches a certain value. In the video, the limit is used to define the derivative, specifically as the process of taking the slope of a secant line between two points on a curve and letting the second point approach the first, thus making the secant line the tangent line.

💡Secant Line

A secant line is a straight line that intersects a curve at two distinct points. In the video, the concept of a secant line is introduced to help understand the derivative. As the second point on the curve approaches the first, the secant line's slope approaches the slope of the tangent line, which is the derivative at that point.

💡Slope

Slope is a measure of the steepness of a line, indicating its incline relative to the horizontal. In the video, the slope is discussed in the context of both secant and tangent lines. The slope of the tangent line at a point on a curve is identified as the derivative at that point, which represents the rate of change of the function.

💡Function

A function in mathematics is a relation between a set of inputs and a set of permissible outputs, with the property that each input is related to exactly one output. In the video, functions are the core objects of study, with the focus on differentiating them to find their derivatives, which describe how the output changes with respect to changes in the input.

💡Difference Quotient

The difference quotient is an expression used in calculus to estimate the derivative of a function at a certain point. It is the ratio of the change in the function's value (delta f) to the change in the input (delta x). In the video, the difference quotient is derived and simplified to find the derivative of the function f(x) = 1/x.

💡Binomial Theorem

The binomial theorem provides a way to expand expressions of the form (a + b)^n. In the video, a small part of the binomial theorem is used to simplify the expression for the difference quotient when finding the derivative of a function like f(x) = x^n. The theorem helps in identifying the terms that contribute to the derivative and those that can be disregarded as 'junk' terms.

💡Polynomial

A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. In the video, the concept of polynomials is extended from the rule for the derivative of x^n to show how to find the derivative of more complex polynomial functions, such as x^3 + 5x^10.

Highlights

Introduction to MIT OpenCourseWare and its mission to provide free educational resources.

Beginning of Unit One on differentiation with an overview of the topics to be covered.

Explaining the concept of a derivative from a geometric perspective, focusing on the tangent line to a curve at a point.

The importance of derivatives in various fields such as science, engineering, economics, and political science.

The goal to teach how to differentiate any function, exemplified by differentiating e^x * arctan(x).

Geometric interpretation of derivatives by finding the tangent line to a graph of a function at a specific point.

Visual representation and the challenge of drawing the tangent line without calculus methods.

The equation of a tangent line and its relation to the derivative, denoted as f'(x_0).

The process of differentiating using the limit of secant lines as Q approaches P.

Introduction of delta notation: delta x (change in x) and delta f (change in f).

Derivation of the formula for the derivative using the difference quotient.

Example calculation of the derivative of the function f(x) = 1/x.

Verification of the derivative result for f(x) = 1/x by analyzing the graph and the behavior as x approaches infinity.

Discussion on the limiting process and its role in defining the derivative.

Addressing the complexity and the 'calculus made harder' aspect through the context of word problems.

Solving a geometry problem involving finding the area of triangles formed by the axes and the tangent to y = 1/x.

Explanation of the symmetry property in the context of the function y = 1/x and its implications for the y-intercept.

Final calculation of the area of the triangle and the surprising result that it is constant regardless of x_0 and y_0.

Introduction of various notations for derivatives, including Newton's notation and Leibniz's notation.

Calculation of the derivative for the function f(x) = x^n and the application of the binomial theorem.

Extension of the derivative rule for x^n to polynomials and the simplification using the binomial theorem.

Clarification on the use of the binomial theorem and its relation to the limit as delta x approaches 0.

Transcripts

Browse More Related Video

01 - Basic Derivatives in Calculus, Part 1 - Learn what a Derivative is and how to Solve Them.

BusCalc 08 Derivative Basics

Worked example: Evaluating derivative with implicit differentiation | AP Calculus AB | Khan Academy

Math 11 - Section 1.5

Techniques for Finding Derivatives

Calculus AB Lesson 4.1: Implicit Differentiation

Related Tags

MIT Calculus Derivatives Geometric Interpretation Physical Interpretation Educational Resources Tangent Line Secant Line Limit Process Binomial Theorem