Circular Motion on an Angle
TLDRIn this grade 12 physics lecture, the instructor explores the concept of circular motion, specifically focusing on a car navigating an inclined on-ramp. Utilizing a new tablet for illustrations, the lecture delves into the physics behind determining the safe speed for a car to take an on-ramp, even under adverse weather conditions like freezing rain. The analysis involves calculating the forces acting on the car, including gravity and the normal force, and how they can be resolved into components to maintain the car's circular motion. The safe speed is derived by setting the centripetal force equal to the gravitational force component and solving for the car's velocity, considering the on-ramp's radius and the angle of inclination.
Takeaways
- 🎨 The lecture is about circular motion, specifically focusing on a car driving on an inclined on-ramp.
- 🚗 The car is depicted as driving out of the screen towards the viewer in a simple illustration.
- 📐 The on-ramp is a circular path with a radius of 300 meters, and the car's mass is 800 kilograms.
- 📊 The incline of the on-ramp is given as an angle theta, which is 11 degrees.
- 🚫 Friction is neglected in the analysis, meaning it is assumed to be zero Newtons.
- 🔍 The forces acting on the car are gravity and the normal force, which are decomposed into X and Y components.
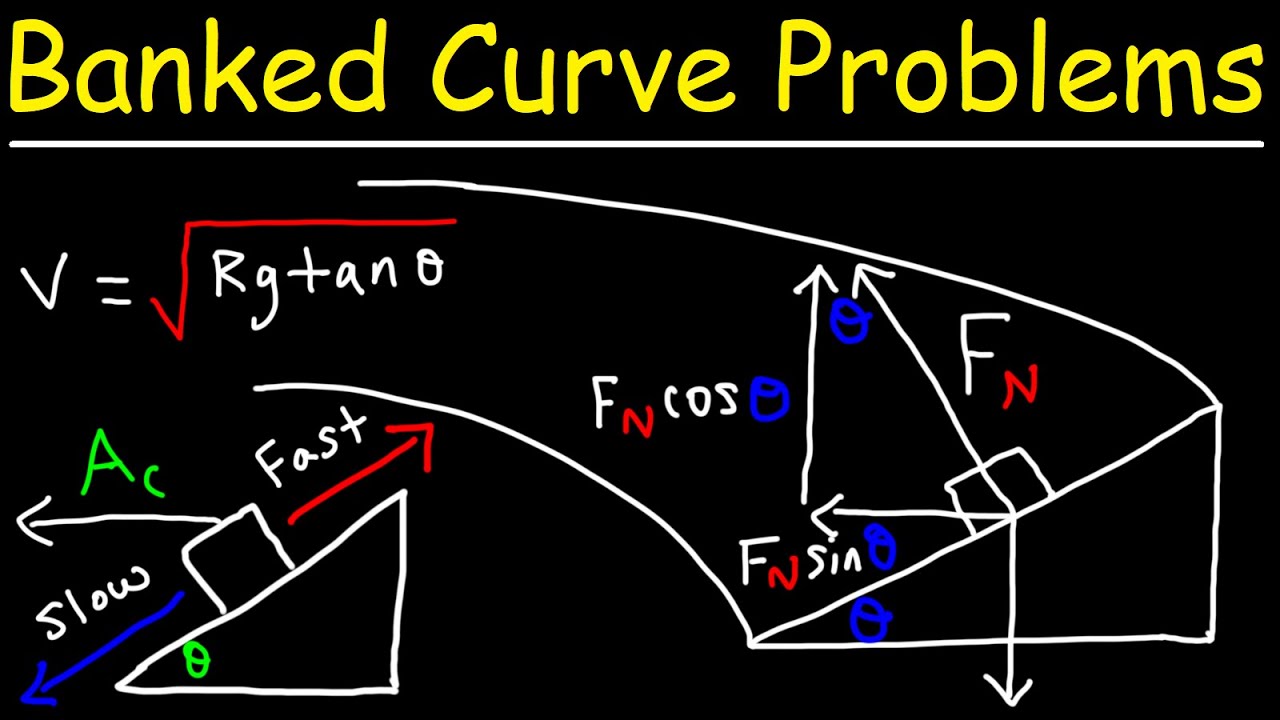
- 🔄 The car's circular motion requires a centripetal force, which is provided by the X component of the normal force.
- 📉 The Y component of the forces must sum to zero since there is no vertical acceleration.
- ⚖️ The normal force is calculated using the equation F_n = M * g / cos(theta), where M is mass, g is gravity, and theta is the incline angle.
- 🔢 The safe speed formula derived is V = √(tan(theta) * g * R), which can be used to calculate the speed at which the car can safely navigate the on-ramp.
- 📚 The lecture uses trigonometry and physics principles to solve for the safe speed of a car in circular motion on an inclined plane.
Q & A
What is the topic of the lecture?
-The topic of the lecture is circular motion, specifically focusing on circular motion and a car on an inclined plane.
What is the purpose of analyzing the circular motion of the car on the on-ramp?
-The purpose is to determine the safe speed at which the car can drive on the on-ramp, taking into account factors such as the radius of the on-ramp and the incline angle, while neglecting friction.
What is the radius of the on-ramp mentioned in the lecture?
-The radius of the on-ramp is given as 300 meters.
What is the mass of the car used in the analysis?
-The mass of the car used in the analysis is 800 kilograms.
What is the incline angle (theta) of the on-ramp?
-The incline angle (theta) of the on-ramp is given as 11 degrees.
Why is friction neglected in this analysis?
-Friction is neglected because the analysis is focused on determining the safe speed regardless of weather conditions, including freezing rain and icy road surfaces where friction would be zero Newtons.
What is the relationship between the normal force and the force causing the car to corner?
-The force causing the car to corner is the X component of the normal force, which can be found by dividing the normal force into components along the X and Y axes.
How is the X component of the normal force (F_nX) related to the angle theta?
-The X component of the normal force (F_nX) is equal to the sine of theta times the normal force (F_n), as it is perpendicular to the inclined plane.
What is the condition for the Y components of the forces to be equal to zero?
-The condition for the Y components of the forces to be equal to zero is that there is no acceleration in the Y direction, meaning the car is not accelerating into the sky or through the floor.
How can you find the safe speed (V) using the given equations?
-The safe speed (V) can be found by solving the equation V^2 = (tan(theta) * g * R) / cos(theta), where g is the acceleration due to gravity and R is the radius of the on-ramp.
What is the significance of the trigonometric identity used in the equation for safe speed?
-The trigonometric identity sine(theta)/cos(theta) = tan(theta) is used to simplify the equation and make it easier to solve for the safe speed (V).
Outlines
🚗 Introduction to Circular Motion and Car on Inclined Plane
This paragraph introduces a lecture on circular motion, specifically focusing on a car driving on an inclined plane, or an on-ramp. The lecturer acknowledges the use of a new tablet which affects the drawing quality. A scenario is presented where a car is driving around an on-ramp, and a cross-sectional view is considered to analyze the circular motion. The car's mass and the radius of the on-ramp are given, along with the incline angle (theta). The goal is to determine the safe speed at which the car can drive on the on-ramp under any weather conditions, assuming no friction. The analysis begins by identifying forces acting on the car, such as gravity and the normal force, and considering the components of these forces in the context of circular motion.
📚 Analyzing Forces and Calculating Safe Speed
The second paragraph delves into the forces acting on the car during its circular motion on an inclined plane. The normal force is broken down into X and Y components, with the X component being crucial for maintaining the car's circular path. The force causing the car to turn is identified as the X component of the normal force (F_nX), which is calculated using the sine of the incline angle (theta). The Y components of the forces are analyzed, leading to an equation where the sum of the Y components equals zero, indicating no vertical acceleration. The normal force (F_n) is then expressed in terms of the car's mass (M), gravitational acceleration (G), and the cosine of theta. Substituting this into the equation for the X components allows for the derivation of an equation relating the safe speed (V), the radius (R), and the trigonometric functions of theta. The safe speed is ultimately found by simplifying and solving this equation, taking into account the car's mass, the radius of the on-ramp, and the angle of incline.
Mindmap
Keywords
💡Circular Motion
💡Inclined Plane
💡Radius
💡Mass
💡Incline (Theta)
💡Safe Speed
💡Friction
💡Force of Gravity
💡Normal Force
💡Components of Forces
💡Trigonometry
Highlights
Introduction to a lecture on circular motion in grade 12 physics.
Exploration of circular motion with a car on an inclined plane.
Use of a new tablet for drawing and explaining concepts.
Visual representation of a car driving on an on-ramp in cross-section.
Assumption of no friction (kinetic friction equals zero Newtons) for the analysis.
Determination of the safe speed to drive a car on an inclined plane.
Given values: radius of 300 meters and car mass of 800 kilograms.
Inclination angle (theta) set at 11 degrees.
Explanation of forces acting on the car: gravity and normal force.
Division of normal force into X and Y components.
Analysis of forces causing the car to corner using trigonometry.
Equation setup for forces in the X direction (F_net,x = mass * v^2 / R).
Calculation of F_nx as sine(theta) * F_n.
Y direction force analysis leading to F_n = M * g / cos(theta).
Derivation of the equation for safe speed (v^2 = sine(theta) * g * R / cos(theta)).
Simplification using trigonometric identity (tan(theta) = sine(theta) / cos(theta)).
Final formula for safe speed (v = sqrt(tan(theta) * g * R)).
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: